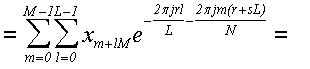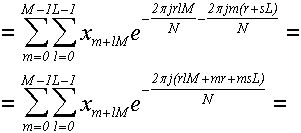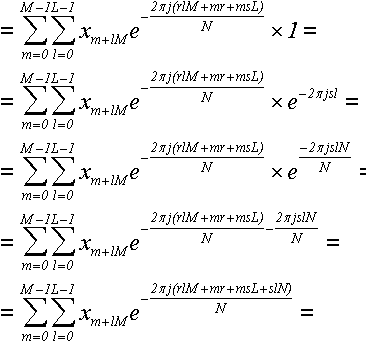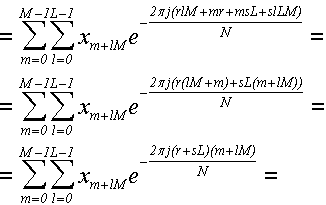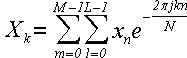Ранее мы рассмотрели случаи, когда число элементов преобразования равно степени двойки. К сожалению, на данный момент
не существует столь же эффективного алгоритма вычисления ДПФ для произвольного N. Однако, существует
алгоритм, который значительно лучше "лобового" решения задачи. Он требует, чтобы N было четным. Допустим,
что N = M 2T = M L. Число L - целая степень двойки, числа M и
T - положительные целые.
Сложность этого алгоритма равна N2 / L + Nlog2L. Как видите, этот алгоритм тем
эффективнее, чем больше L, то есть, чем больше число элементов N "похоже" на степень двойки.
В худшем случае, когда L = 2, он лишь немногим лучше "лобового" решения, которое имеет сложность
N2.
Тем не менее, на практике нам часто полезен именно описанный алгоритм. Допустим, у нас имеется оцифрованный звуковой
сигнал, длиной в 2001 отсчет, и мы хотим узнать его спектр. Если мы применим обычный алгоритм, то нам придется
отрезать "лишний" кусок сигнала, размером почти в его половину, уменьшив число отсчетов до 1024. Но в таком случае мы потеряем гармоники, которые,
возможно, возникли только ближе к концу сигнала. Другой вариант: дополнить исходный сигнал до 2048 отсчетов - тоже плох. В
самом деле: чем его дополнить? Если нулями, то в результате мы приобретем множество лишних гармоник из-за резкого
скачка сигнала вниз на 2001-м отсчете. Совершенно неясно, как интерполировать сигнал на дополнительные 47 отсчетов так,
чтобы не появились новые, ненужные гармоники (шумы). И только новый алгоритм решает эту проблему. С помощью него мы
можем "отрезать" совсем небольшой кусочек, в 1 отсчет, взяв L = 16 и получив ускорение в 16 раз! Либо
мы можем пожертвовать кусочком чуть длиннее, взяв L еще больше. Для реальных сигналов невелика вероятность,
что на этом маленьком отрезке спектр резко изменится, так что результат получится вполне удовлетворительный.
Теперь рассмотрим сам алгоритм. Его главной частью является уже знакомый нам алгоритм "fft" для N, равного
степени двойки. Этот алгоритм лишь немного модифицирован. Из исходной последовательности длиной N
выбирается L элементов, начиная от элемента с номером h (0 ≤ h < M) и с шагом M. В
результате получается последовательность из L элементов. Так как L у нас - степень двойки,
мы можем применить к полученной последовательности обычный алгоритм БПФ. Результаты преобразования записываются в
те же ячейки, откуда были взяты. Изменение алгоритма заключается всего лишь в том, что каждый раз вместо
g-го элемента берется элемент с номером h + gM, то есть, выполняется замена индексов по
формуле:
g → h + gM (38)
Позднее мы еще дополнительно оптимизируем этот алгоритм, а пока выпишем его результат в виде формулы:
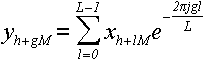 (39)
(39)
Где g = 0, 1,..., L - 1.
Как видите, по сравнению с формулой (1) мы выполнили замену переменных: k → g, n → l, N → L и сделали
преобразование индексов по формуле (38).
На первом этапе модифицированный алгоритм БПФ применяется ко всем элементам исходной последовательности. Для этого
вычисление по формуле (38) выполняется для h = 0, 1,..., M - 1. Каждое такое вычисление меняет
L элементов с индексами h, h + M, h + 2M,..., h + (L - 1)M. Таким образом, вызвав
M раз этот алгоритм, мы изменим все N = ML элементов заданной последовательности:
Шаг 0: элементы с номерами 0, M, 2M, ... (L-1)M
Шаг 1: элементы с номерами 1, 1 + M, 1 + 2M, ... 1 + (L-1)M
Шаг 2: элементы с номерами 2, 2 + M, 2 + 2M, ... 2 + (L-1)M
...
Шаг M-1: элементы с номерами M - 1, M - 1 + M, M - 1 + 2M, ... M - 1 + (L-1)M
На втором этапе заводится новый массив размером в N элементов, и к нему применяется формула:
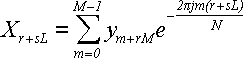 (40)
(40)
В двойном цикле величина s проходит значения 0..M - 1, а величина r проходит
значения 0..L - 1. Общее число итераций, таким образом, равно ML = N. Каждая итерация требует
суммирования M элементов. То есть, общее количество слагаемых равно NM.
На предварительном этапе мы M раз применили обычный алгоритм БПФ для L элементов, который,
как мы уже знаем, имеет сложность L log2L. Таким образом, общая сложность алгоритма
равна:
NM + L log2L = N(N/L) + ML log2L = N2/L + N log2L.
Тем самым, мы доказали формулу сложности, приведенную в начале главы.
Теперь нам осталось доказать только то, что формула (40) действительно дает ДПФ. Для этого подставим формулу
(39) в формулу (40):
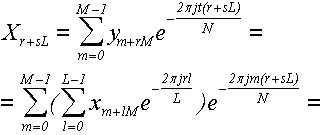
... поскольку выражение 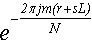 не зависит от l, то мы
его можем внести под знак внутренней суммы:
не зависит от l, то мы
его можем внести под знак внутренней суммы:
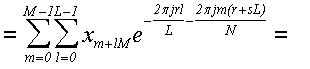
... теперь учтем, что L = N/M, чтобы привести выражение в показателе степени к общему знаменателю и упростить:
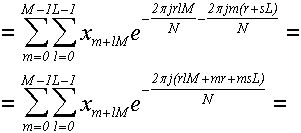
... теперь воспользуемся Теоремой 0, чтобы добавить полезный множитель, равный единице:
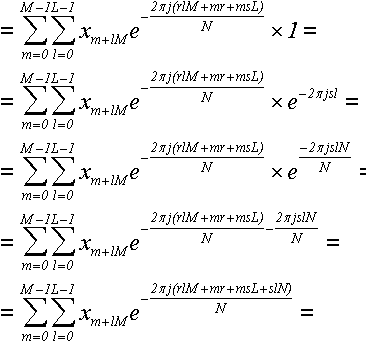
... теперь воспользуемся равенством N = ML, чтобы разбить сумму в числителе на множители:
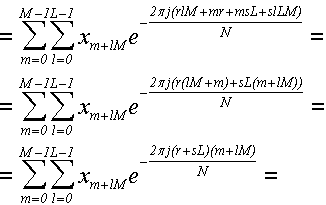
... теперь выполним замену переменных r + sL → k, m + lM → n:
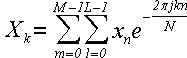
Эта сумма эквивалентна сумме (1), с точностью до перемены мест слагаемых. В самом деле, если
n = m + lM, m = 0..M - 1, l = 0..L - 1, N = LM, то переменная n по мере суммирования
принимает все значения от 0 до N - 1 ровно по одному разу. Что и требовалось доказать.
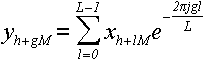 (39)
(39)
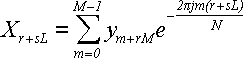 (40)
(40)
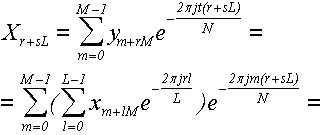
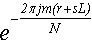 не зависит от
не зависит от