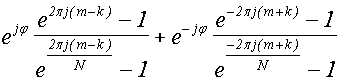Что такое эффект размазывания.
В предыдущей главе мы рассматривали ситуацию, когда частота
колебания равнялась m/T, где m - целое.
Теперь рассмотрим ситуацию, когда это не так. Положим, что
m = n + q, где n - целое и 0 < q < 1.
Воспользуемся формулой (35). Поскольку первые несколько
условий для нецелого m не выполняются, то
остается последняя, самая сложная формула, помеченная словами
"Для остальных k":
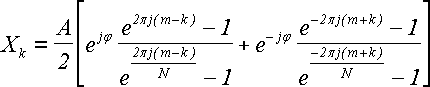
Подставим в эту формулу n + q
вместо m и выполним упрощения,
воспользовавшись формулой (34) и введя обозначение ρ = 2πj.
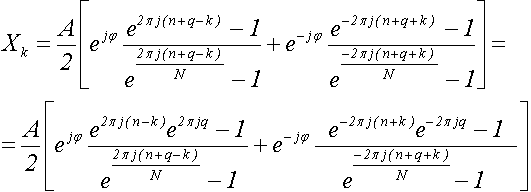
Итого:
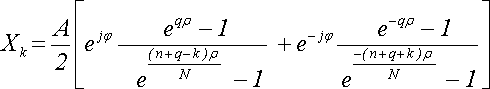, ρ = 2πj (37)
Теперь построим график функции, чтобы понять, как
она себя ведет. Ниже показана трехмерная поверхность.
По горизонтальной оси отложено k,
по вертикальной |Xk| и по
оси, уходящей вглубь плоскости, отложено q
от 0.01 до 0.99.
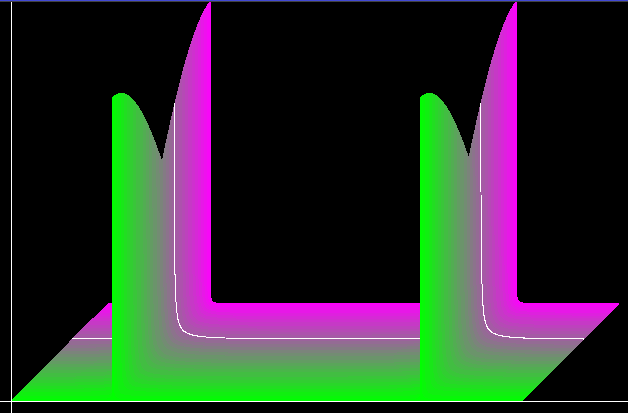
Рис. 1.
На рисунке видно два ярко выраженных ребра. Первое из них
всегда приходится на k = n и k = n + 1.
Второе ребро получается в результате зеркального эффекта.
Высота пика наименьшая в окрестности q = 0.5.
А наибольшая в окрестности q = 1 и q = 0
- то есть при целочисленном m.
К сожалению, пик не является единственным ненулевым коэффициентом
Фурье. Рядом с ним есть множество меньших, но не нулевых величин.
Если при целочисленном m можно наблюдать единственную
полоску, то при нецелом m = n + q эта полоска
размазывается:
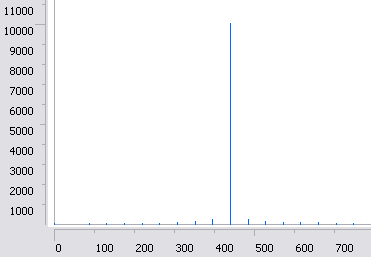
Рис. 2.
На рисунке приведена практическая ситуация. Это - ДПФ для звука,
содержащегося в обычном WAV-файле. Высота синего штриха цвет соответствует
|Xk|. Исходный сигнал содержал
ноту "ля" второй октавы с частотой 440 гц и фазой в 90 градусов. ДПФ было
выполнено для N = 1000. Однако частота дискретизации
звука в WAV-файле составляла 44100 Гц, так что период дискретизации
был равен T = 1000/44100 секунд и из формулы m/T = 440
получим m = 440*(1000/44100) = 9.97,
то есть, не целое. В результате ярко выраженный пик окружают дополнительные
ненулевые значения.
На следующем рисунке:
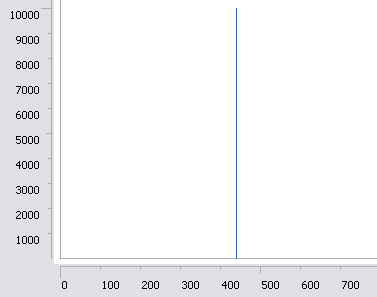
Рис. 3.
показана "хорошая" ситуация, когда частота исходного звука составляла 441 Гц,
и m = 441*1000/44100 = 10, то есть целое. Вы видите только один
ненулевой отсчет.
Этот эффект будем называть эффектом размазывания. Вы видите, что он
определяет погрешность, с которой можно найти частоту
исходного колебания. Погрешность равна 1/T. При достаточно
большом отклонении m от целого эффект может быть очень заметен.
Например ниже вы видите ДПФ для сигнала, соответствующего ноте "ля-бемоль":
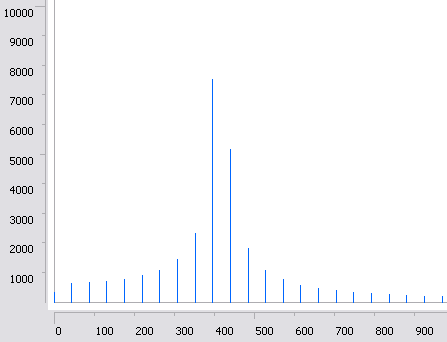
Рис. 4.
Точнее можно попытаться определить параметры m,
A и φ численными методами.
Для поиска φ следует учесть, что изменение
A не повлияет на комплексную фазу (аргумент)
коэффициентов Xk.
В самом деле, мы можем представить коэффициенты в виде:
Xk = (A/2)Z(m,φ)k,
где Z(m,φ)k - комплексное число, не зависящее
от действительного числа A, но зависящее
от m и φ:
Z(m,φ)k =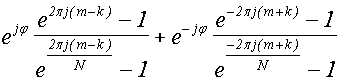 
Также не зависит от A отношение коэффициентов
Xk/Xl = Z(m,φ)k/Z(m,φ)l.
Это значит, что у нас есть две целевые функции, с помощью которых
мы можем найти частоту m/T и фазу φ.
Возьмем Xk, максимальное по модулю. Если соседние
отсчеты Xk-1 и Xk+1
равны нулю, то у нас нет эффекта размазывания и параметры
восстанавливаются так, как описано в предыдущей главе. На самом деле
нам придется сравнивать не с нулем, а с некоторым малым числом, поскольку
некоторая погрешность при вычислении ДПФ неизбежна.
Теперь, когда мы убедились в наличии эффекта размазывания, попробуем найти
m и φ после чего восстановим A
по формуле: A = |2Xk / Z(m,φ)k|.
Сначала найдем два максимальных
отсчета Xk и Xk+1.
Теперь мы знаем, что искомое m лежит на
интервале (k, k+1).
Для нахождения m и φ нужно численно решить
систему уравнений:
|Z(m,φ)k/Z(m,φ)k+1| = |Xk/Xk+1|
Arg(Z(m,φ)k) = Arg(Xk)
Здесь только две неизвестных - m и φ, неизвестная A исключена.
Систему можно решить итерационно. Для этого сначала фиксируем φ и подбираем m,
которое удовлетворяет первому уравнению системы. Потом - наоборот фиксируем найденное m и
подбираем φ, которое удовлетворяет второму уравнению системы. Потом снова возавращаемся
к первому уравнения - до тех пор, пока оба уравнения не окажутся сбалансированы с достаточной точностью.
Также существует метод вычисления частоты m, основанный на сопоставлении фаз. Стефан Бернси использует его
в своем алгоритме транспонирования.
Данный метод быстрее (не требует нескольких итераций для решения системы уравнений), однако требует двух
преобразований Фурье для одного фрагмента с небольшим сдвигом на время ΔT. Этот
алгоритм предполагает, что спектр не меняется за это короткое время - хотя бы в отношении частот.
Допустим, у нас есть фрагмент длиной T. Мы делаем преобразование Фурье не для всего этого
фрагмента, а для двух перекрывающихся фрагментов [0, T - ΔT] и [ΔT, T].
Затем рассматриваем каждую получившуюся гармонику и ее фазу в первом и втором преобразовании. По величине
сдвига фазы вносится поправка q и вычисляется точная частота (n + q)/T.
Наконец, эффект размазывания можно уменьшить, если применять оконные функции.
Хотя в результате применения
оконной функции, спектр может сильно исказиться, но все-таки форма пиков изменяется, сужается их "подошва".
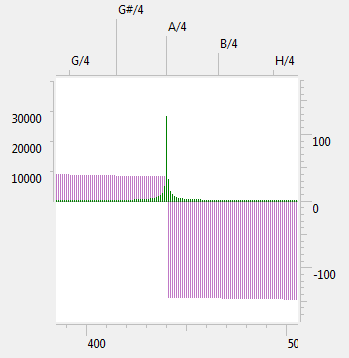
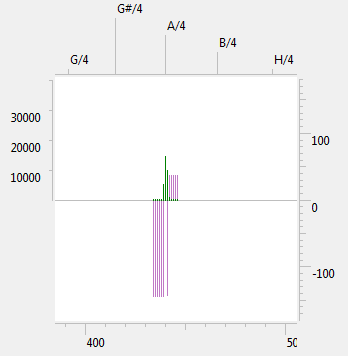
Вот пример для T = 1 сек, N = 44100, m/T = 440.2 Гц, φ = 0.
Слева - спектр с "размазыванием", полученный обычным ДПФ. Справа - с применением оконной функции Хамминга.
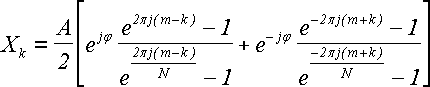
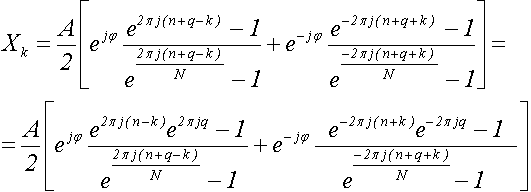
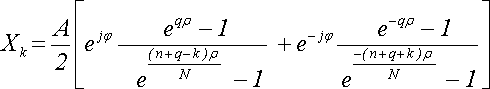