Настало время написать и оптимизировать алгоритм. Посмотрите на исходный алгоритм "fft" и
на алгоритм для случая четного N "fft2".
Здесь мы рассмотрим листинг "fft2" сверху вниз, комментируя все детали.
Сверху вы видите фрагмент, совпадающий со старым листингом вплоть до #define M_2PI. Этот макрос
определяет константу 2π.
Функция complex_mul выполняет умножение комплексных чисел z1 и z2 и записывает
результат в ячейку z.
Мы собираемся вызывать алгоритм "fft" M раз для одного и того же числа элементов L.
Для оптимизации мы должны вынести за пределы алгоритма "fft" те действия, которые не зависят от выбора конкретных
элементов в массиве.
К таким действиям можно отнести выделение памяти для хранения поворачивающих множителей и освобождение ее.
Деление результата на N также можно выполнить позже для всего массива сразу. А главное, мы можем всего
лишь однажды вычислить все поворачивающие множители. Для решения этой задачи мы напишем отдельную функцию
createWstore, которая и вычисляет множители, и выделает массив ячеек памяти для них. Позднее этот
массив будет передаваться как параметр в новый вариант алгоритма "fft".
Функция createWstore представляет собой ту часть основного цикла "fft", которая отвечала за рассчет
поворачивающих множителей. Однако, она оптимизирована. Число итераций меньше, чем в исходном алгоритме,
поскольку не на всех итерациях выполнялось вычисление нового множителя, иногда происходило только копирование.
Поэтому шаг приращений индекса в массиве вдвое больше: Skew2 вместо Skew.
Переменная k для определения четности/нечетности нам больше не нужна, так что внутренний цикл
останавливается при достижении границы массива WstoreEnd.
Порядок вычисления множителей 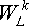 будет понятнее на примере. Если
L = 32, то порядок изменения k такой (точкой с запятой разделены итерации внешнего цикла,
а запятой - внутреннего):
будет понятнее на примере. Если
L = 32, то порядок изменения k такой (точкой с запятой разделены итерации внешнего цикла,
а запятой - внутреннего):
k = 0; 16; 8, 24; 4, 12, 20, 28; 2, 6, 10, 14, 18, 22, 26; 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23...31
Далее, вместо старого алгоритма "fft" мы напишем новый - "fft_step" с учетом того, что поворачивающие множители
считать не надо, и не надо делить результат на N.
Сам алгоритм практически не изменился за исключением того, что все расстояния между элементами
массива увеличились в M раз, согласно формуле (38). Приставка "M" перед именами
новых переменных означает умножение на M.
На вход этой функции будет передаваться массив со смещением. Тем самым происходит коррекция индекса
на +h элементов, согласно формуле (38).
В основной функции сначала анализируется параметр N. Если он нечетный, то мы вынуждены отсечь
один элемент (последний) и уменьшить N на единицу. Таким образом, на входе алгоритма требуется
N ≥ 2.
Далее вычисляется L как максимальная степень двойки, кратная N, сама эта степень
T и величина M.
Затем вычисляются поворачивающие множители для "fft_step" и вызывается сам "fft_step" нужное число раз. Если
оказывается, что N является степенью двойки, то сработает обычный "fft".
Следующим шагом мы вычисляем поворачивающие коэффициенты уже для формулы (40). Этот фрагмент алгоритма очень
похож на createWstore, поэтому в дополнительных комментариях не нуждается. Результат оказывается
в массиве mult.
Далее вычисляется формула (40). Смысл переменных: pX - указатель на Xr+sL;
rpsL = r + sL; mprM = m + rM; one - очередное слагаемое суммы (40).
Величина widx равна остатку от деления m(r + sL) на N. Таким способом
мы избегаем выхода за границы массива mult. Это можно делать, благодаря Теореме 1 - ведь
поворачивающие множители как раз имеют период N.
Еще можно заметить, что в сумме (40) в первом множителе поворачивающий коэффициент всегда равен 1,
благодаря чему мы экономим несколько умножений.
И наконец, происходит корректировка результатов для обратного ДПФ делением на N.
Функция БПФ для четного N называется "fft2".
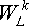 будет понятнее на примере. Если
будет понятнее на примере. Если