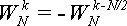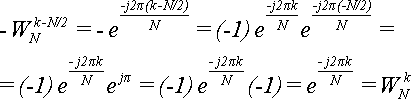Рассмотрим ряд свойств поворачивающих множителей, которые нам понадобятся в дальнейшем.
Верхняя цифра в поворачивающем множителе не является индексом, это - степень. Поэтому, когда она равна единице, мы не будем ее писать:
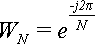
Прямое преобразование Фурье можно выразить через поворачивающие множители. В результате формула (1) примет вид:
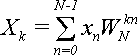 (3).
(3).
Эти коэффициенты действительно оправдывают свое название. Нарисуем на комплексной плоскости любое
комплексное число, в виде вектора, исходящего из начала координат. Представим это комплексное число
в показательной форме:
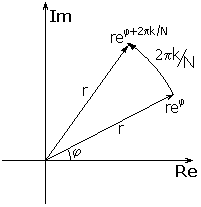
Теперь возьмем какой-нибудь поворачивающий множитель 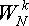 .
Его модуль равен единице, а фаза -
.
Его модуль равен единице, а фаза -
Если теперь посмотреть на формулу (3), то станет ясен геометрический смысл преобразования Фурье: он состоит в том,
чтобы представить
Если комплексное число представлено в виде
По формуле Эйлера, и ввиду периодичности синуса и косинуса:
Величина 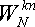 периодична по
периодична по
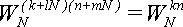 (4).
(4).
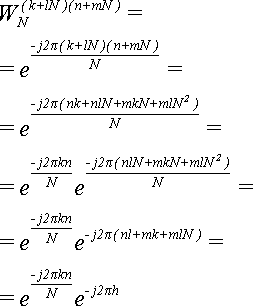 (5)
(5)
Величина
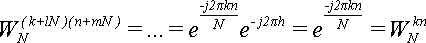
Что и требовалось доказать по (4).
Для величины 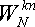 справедлива
формула:
справедлива
формула: