Вывод основных формул

[предыдущая глава]  [оглавление]  [следующая глава]

Алгоритм быстрого преобразования Фурье (БПФ) - это оптимизированный по скорости способ вычисления ДПФ. Основная идея заключается в двух пунктах.

1. Необходимо разделить сумму (1) из N слагаемых на две суммы по N/2 слагаемых, и вычислить их по отдельности. Для вычисления каждой из подсумм, надо их тоже разделить на две и т.д.
2. Необходимо повторно использовать уже вычисленные слагаемые.

Применяют либо "прореживание по времени" (когда в первую сумму попадают слагаемые с четными номерами, а во вторую - с нечетными), либо "прореживание по частоте" (когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные). Оба варианта равноценны. В силу специфики алгоритма приходится применять только N, являющиеся степенями 2. Рассмотрим случай прореживания по времени.

---

Теорема 3.

Определим еще две последовательности: {x_[even]} и {x_[odd]} через последовательность {x} следующим образом:

x_[even]n = x_2n,
x_[odd]n = x_2n+1,     (6)
n = 0, 1,..., N/2-1

Пусть к этим последовательностям применены ДПФ и получены результаты в виде двух новых последовательностей {X_[even]} и {X_[odd]} по N/2 элементов в каждой.

Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X_[even]} и {X_[odd]} по формуле:

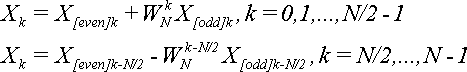    (7).

Доказательство:

Начинаем от формулы (2), в которую подставляем равенства из (6):

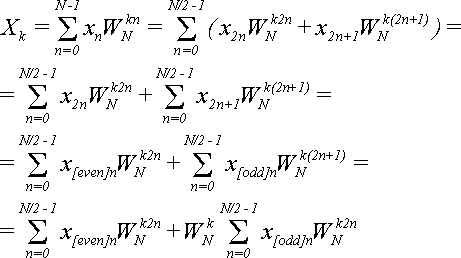    (8)

Теперь обратим внимание на то, что:

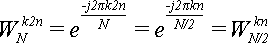    (9)

Подставляя (9) в (8) получаем:

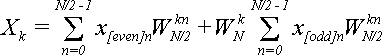    (10)

Сравним с формулами для X_[even]k и X_[odd]k при k = 0,1,…,N/2-1:

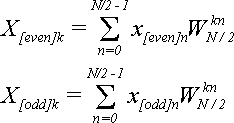    (11)

Подставляя (11) в (10) получим первую часть формулы (7):

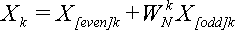
Это будет верно при k = 0,1,…,N/2-1.

Согласно теореме 1:

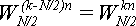    (12)

Подставим (12) в (10), и заменим 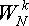по теореме 2:

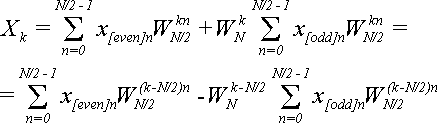    (13)

Для k = N/2,…,N-1 по формуле (2):

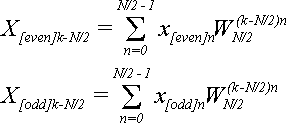    (14)

Подставляем (14) в (13):

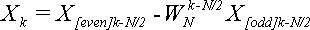
Эта формула верна для k = N/2,…,N-1 и, соответственно, (k - N/2) = 0,1,…,N/2-1 и представляет собой вторую и последнюю часть утверждения (7), которое надо было доказать.

---

Формула (7) позволяет сократить число умножений вдвое (не считая умножений при вычислении X_[even]k и X _[odd]k), если вычислять X_k не последовательно от 0 до N - 1, а попарно: X₀ и X_N/2, X₁ и X_N/2+1,..., X_N/2-1 и X_N. Пары образуются по принципу: X_k и X_N/2+k.

---

Теорема 4.

ДПФ можно вычислить также по формуле:

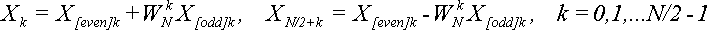    (15)

Доказательство:

Согласно второй части формулы (7), получим:

 

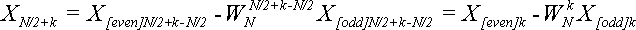
Это доказывает второе равенство в утверждении теоремы, а первое уже доказано в теореме 3.

---

Также по этой теореме видно, что отпадает необходимость хранить вычисленные 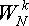X_[even]k и X_[odd]k после использования при вычислении очередной пары и одно вычисление можно использовать для вычисления двух элементов последовательности {X}.

На этом шаге будет выполнено N/2 умножений комплексных чисел. Если мы применим ту же схему для вычисления последовательностей {X_[even]} и {X_[odd]}, то каждая из них потребует N/4 умножений, итого еще N/2. Продолжая далее в том же духе log₂N раз, дойдем до сумм, состоящих всего из одного слагаемого, так что общее количество умножений окажется равно (N/2)log₂N, что явно лучше, чем N² умножений по формуле (2).

Рассмотрим БПФ для разных N. Для ясности добавим еще один нижний индекс, который будет указывать общее количество элементов последовательности, к которой этот элемент принадлежит. То есть X_{R}k - это k-й элемент последовательности {X_{R}} из R элементов. X_{R}[even]k - это k-й элемент последовательности {X_{R}[even]} из R элементов, вычисленный по четным элементам последовательности {X_{2R}}. X_{R}[odd]k - это k-й элемент последовательности {X_{R}[odd]}, вычисленный по нечетным элементам последовательности {X_{2R}}.

В вырожденном случае, когда слагаемое всего одно (N = 1) формула (1) упрощается до:

,

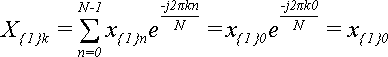Поскольку в данном случае k может быть равно только 0, то X_{1}0 = x_{1}0, то есть, ДПФ над одним числом дает это же самое число.

Для N = 2 по теореме 4 получим:

(откуда берутся X_{2}[even]0 и т.д. см. пояснение чуть ниже)

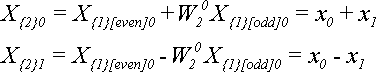
Для N = 4 по теореме 4 получим:

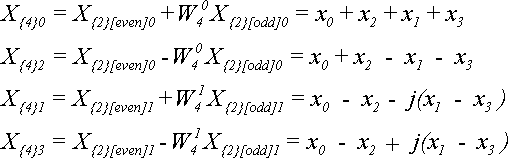
Отсюда видно, что если элементы исходной последовательности были действительными, то при увеличении N элементы ДПФ становятся комплексными.

Поясним, откуда получились X_{2}[even]0,...

Была исходная последовательность:

x0, x1, x2, x3

Она была разделена на две - четную (even) и нечетную (odd), в каждой по 2 элемента:

even	odd
x0, x2	x1, x3

Эти последовательности тоже были поделены на последовательности по 1 элементу:

even	odd
even odd x0 x2	even odd x1 x3

Как выше пояснялось, преобразование над одним числом дает то же самое число. То есть, получается то же самое, но это уже как бы преобразованные последовательности по 1 элементу. Теперь применяется формула для N = 2, чтобы из последовательностей по 1 элементу сделать последовательности по 2 элемента, но уже прошедшие преобразование Фурье:

even	odd
x0 + x2, x0 - x2	x1 + x3, x1 - x3

Вот эти две последовательности и дают нам искомые переменные. Ниже они показаны в тех же ячейках таблицы:

even	odd
X{2}[even]0, X{2}[even]1	X{2}[odd]0, X{2}[odd]1

Для N = 8 по теореме 4 получим:

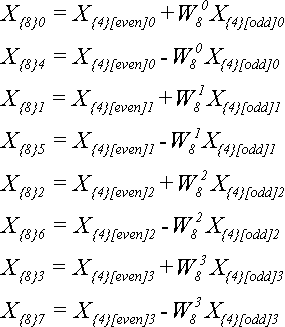
Принцип вычисления тот же самый: разбиение на последовательности по 4, 2, 1 элементу, а затем - преобразование обратно в последовательности по 1, 2, 4 элемента. На каждом этапе выполняются попарные сложения и вычитания, а меняются только W-коэффициенты.

Обратите внимание, что на предыдущем шаге мы использовали степени W₄, а на этом - степени W₈. Лишних вычислений можно было бы избежать, если учесть тот факт, что

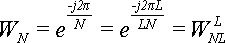
Тогда формулы для N=4 будут использовать те же W-множители, что и формулы для N=8:

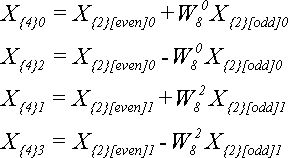
Подведем итог:

В основе алгоритма БПФ лежат следующие формулы:

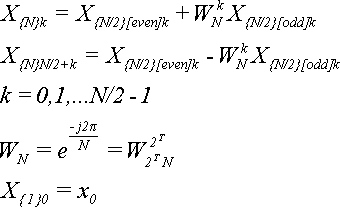    (16)