2. Первая форма дробного
пуассоновского процесса
Построим первый тип дробного пуассоновского процесса (который мы
определили как Nν (t), t>0) с помощью замены в
дифференциальных уравнениях, управляющих классическим пуассоновским процессом,
обычных производных на дробные, определенные формулой (1.3), то есть на
производные Dzerbayshan-Caputo.
Таким образом, нас интересует решение уравнений:
![]()
где
p−1(t) = 0 и с начальными условиями:

Использование определения (1.3)
позволяет нам избавиться от дробной производной в начальных условиях и получить
другие, более удобные с вероятностной точки зрения выражения для решения.
Дифференциальное уравнение для
производящей функции в стандартном случае
![]()
мы
заменим на следующее уравнение:
![]()
с
начальным условием G(u,0) = 1.
Применим преобразование Лапласа к решению
(2.4):
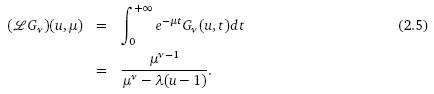
Обратное преобразование Лапласа,
примененное к (2.5), дает следующую производящую функцию:
![]()
Уникальность решений (2.4) может быть доказана с помощью предположения
о существовании двух решений (G1 и G2) и решения задачи Коши для h(u, t) = G1(u, t) - G2(u, t), с начальным условием h(u, 0) =
0. Существование решения следует из нашего анализа.
Из формулы (2.6) можно почерпнуть немало информации: некоторые
следствия очевидны:
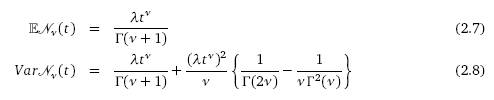
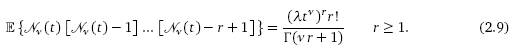
Обратим внимание, что обычное
уравнение между мат. ожиданием и дисперсией отсутствует в этой модели, в то
время, как при ν
= 1 оно может быть записано как E
N1
(t)
= Var
N1
(t).
Наиболее интересный результат –
функция распределения, связанная с (2.6):
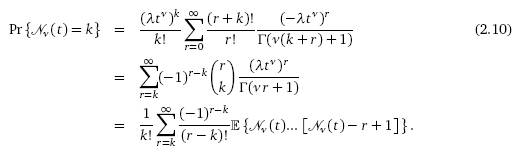
Для небольших k можно
записать распределение (2.10) в терминах функций Миттаг-Лефлера:
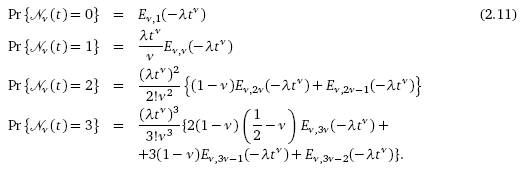
Теперь получим
удобное представление решения (2.1)-(2.2), дающее интересную вероятностную
интерпретацию для родственного процесса. Следующий результат показывает важную
связь между дробным пуассоновским процессом и дробными уравнениями диффузии.
Определим
ν2ν = ν2ν(y, t) решение следующей задачи Коши:
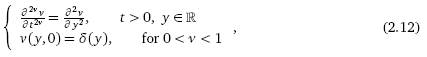
с
дополнительным условием
![]()
Условие (2.13) обусловлено применением
преобразования Лапласа дробной производной (см. Podlubny (1999), формула (2.253),
стр.106)
Хорошо известно, что
![]()
где
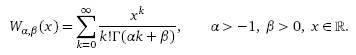
Теорема
2.1
Пусть
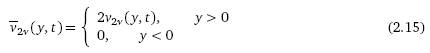
– свернутое
решение (2.12), тогда производящая функция дробного пуассоновского процесса Nν (t), t>0, может
быть записано в виде:
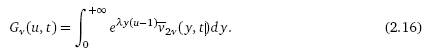
Соответствующее
распределение, при k ≥ 0,
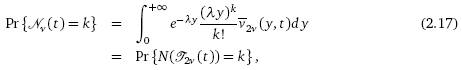
где ![]() t > 0, описывает случайное время с плотностью
перехода, заданной формулой (2.15).
t > 0, описывает случайное время с плотностью
перехода, заданной формулой (2.15).
…………………………