Технический перевод

Операции с матрицами: программирование на C++

Главная

8. Статический расчет фермы

Статический расчет фермы заключается в определении реакций в ее опорах и нахождении усилий в ее стержнях.

Для статически определимых ферм для решения данной задачи, как известно, достаточно только уравнений равновесия. Составив для каждого узла по два уравнения равновесия проекций всех сил на вертикальную и горизонтальную оси, получим замкнутую систему уравнений, решив которую найдем усилия во всех стержнях фермы и реакции опор. Данный алгоритм может быть относительно просто реализован в виде программы для ЭВМ. Кроме того, статический расчет фермы может быть выполнен с применением программных комплексов на основе метода конечных элементов.

В то же время, при расчете ферм с небольшим количеством стержней, а также при проверке результатов расчетов, полученных на ЭВМ, может потребоваться использование простейших приемов определения усилий в стержнях ферм. При расчете простых ферм используются методы вырезания узлов, сквозных сечений, совместных сечений, замены стержней и др. Здесь рассмотрим только два метода: метод вырезания узлов и метод сечений.

8.1. Метод вырезания узлов

Метод вырезания узлов уже использовался нами при статическом анализе геометрической неизменяемости фермы. Он заключается в мысленном вырезании узла фермы с заменой действия на него стержней соответствующими внутренними усилиями. Эти усилия связаны между собой и приложенной к стержню внешней нагрузкой (или опорными реакциями) посредством статических уравнений равновесия. Для любого узла можно составить два таких уравнения - равенства нулю суммы проекций всех сил, например, на вертикальную и горизонтальную оси ΣX=0 и ΣY=0. Очевидно, если в узле сходятся два стержня, то из этих уравнений могут быть найдены усилия в обоих из них. Если узел соединяет три стержня, но усилие в одном из них уже найдено из рассмотрения равновесия другого узла или использованием способа сечений, то из этих двух уравнений могут быть найдены усилия в двух оставшихся стержнях. После этого можно вырезать следующий узел и продолжить расчет.

В методе вырезания узлов необходимо установить порядок вырезания узлов. Например, для расчета фермы (рис. 8.1, а) сначала вырежем узел A (рис. 8.1, б) и запишем уравнения равновесия:

ΣX = N_A-10+N_A-1 ∙cos𝛼=0;

ΣY = N_A-1 ∙sinα+1,5P=0.

Из них: N_A-1= –1,5P/sinα;  N_A-10=1,5P/tgα.

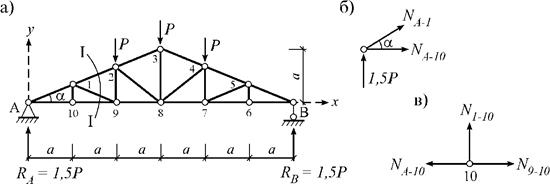
Рис. 8.1

Теперь вырежем узел 10 (рис. 8.1, в) и запишем условия равновесия

ΣX = N_9-10 –N_A-10=0;

ΣY = N_1-10=0.

Из них получаем: N_9-10 =N_A-10=1,5P/tgα;   N_1-10=0.

После этого можно вырезать узлы 1, 9, 2, 3, 8, 4, 7, 6, 5.

У метода вырезания узлов есть недостаток: ошибка (неточность), допущенная при расчете одного узла, влияет на последующие вычисления. Поэтому результаты, полученные этим методом, надо контролировать. Например, результаты расчета фермы могут быть проверены по формуле

ΣN_il_i = ΣP_x∙x+ΣP_y∙y,

 где N_i – усилия в стержнях, l_i – длины стержней, P_x и P_y – проекции нагрузок (включая и опорные реакции), x и y – координаты нагрузок.

Из метода вырезания узлов вытекают несколько признаков (частных случаев), упрощающих расчет ферм:

1) если в узле сходятся два стержня и внешняя нагрузка не приложена (рис. 8.2, а), то оба усилия равны нулю: N₁= N₂=0;

2) если в узле сходятся два стержня, а внешняя нагрузка действует в направлении одного стержня (рис. 8.2, б), то N₁=P, N₂=0;

3) если в трехстержневом узле два стержня лежат на одной прямой, а внешней нагрузки нет (рис. 8.2, в), то усилия в двух стержнях равны: N₁= N₂, а усилие в боковом стержне равно нулю: N₃=0;

4) если в четырехстержневом узле стержни попарно лежат на одной прямой, а внешней нагрузки нет (рис. 8.2, г), то усилия также попарно равны между собой: N₁= N₂,N₃= N₄.

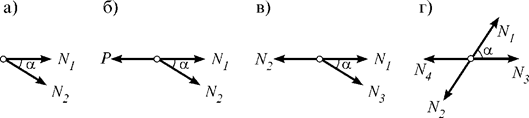
Рис. 8.2

Используя эти признаки легко определяются некоторые усилия рассмотренной фермы (рис. 8.1, а):

– по 2-му признаку N_1-10=N_1-9=N_2-9=0;   N_5-6=N_5-7=N_4-7=0;

– по 3-му  признаку N_A-10=N_9-10=N_8-9;   N_B-6=N_6-7=N_7-8;   N_A-1=N_1-2;   N_B-5= N_4-5.

8.2. Метод сквозных сечений

Метод сквозных сечений состоит в мысленном рассечении фермы на две части и рассмотрении равновесия одной из них. При этом действие отбрасываемой части нарассматриваемую должно быть заменено усилиями в стержнях ферм. Если провести сечение таким образом, чтобы оно проходило через три стержня, то можно составить уравнения равновесия для рассматриваемой части фермы таким образом, чтобы найти усилия во всех трех стержнях. Так, в точке пересечения направлений двух из них составляется уравнение момента, из которого определяется третье усилие. Точка, в которой  составляется уравнение момента, называется моментной точкой.

В качестве примера рассмотрим ту же ферму, проведя через нее сквозное сечение I–I (рис. 8.1, а). Рассматривая равновесие левой части от сечения (рис. 8.3), составим уравнение момента в точке 1:

ΣM₁ = N_9-10∙a/3 – 1,5P∙a=0. 

Отсюда получаем: N_9-10=4,5P .

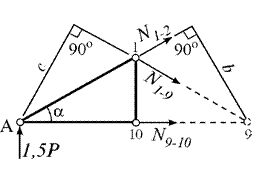
Рис. 8.3

Точка 9 является моментной точкой для N_1-2. Поэтому

ΣM₉ = –N_1-2∙b –1,5P∙2a=0.

Так как b=2a×sinα, получаем   N_1-2=–1,5P/ sin𝛼.

Для N_1-9: ΣM_A = –N_1-9∙c=0. Отсюда получаем N_1-9=0.

Иногда (например, когда два стержня параллельны) моментной точки не существует. В этом случае вместо уравнения момента следует составлять уравнение проекции на ось, перпендикулярную этим параллельным стержням.

У метода сквозных сечений есть один недостаток: в сложных фермах не удается провести такое сквозное сечение, чтобы появились только три неизвестных усилия. В этом случае некоторые неизвестные нужно определять заранее или использовать другие методы (методы совместных сечений или замены связей).

Таким образом, усилие в любом стержне статически определимой фермы может быть определено в один или несколько шагов путем последовательных вырезаний узлов и/или рассмотрением равновесия отсеченных определенным образом частей фермы.

Очевидно, при использовании этих способов необходимо предварительное определение опорных реакций из уравнений равновесия фермы.