Домой

Числа в троичном представлении Стахова

Класс FFT - расчет спектра методом БПФ на C++

Переводы с английского математических и технических статей

---

DMatrix – класс для работы с динамическими матрицами

Калюжный О.Н.

oleg314@mail.ru

Скачать класс DMatrix

Класс DMatrix - применение в вибродиагностике двигателей

Внимание! Об обновлениях смотри внизу этой страницы. Последнее обновление – от 18.04.2018.

Введение

Класс DMatrix разработан на языке C++ (в среде Borland Builder6) и предназначен для встраивания в исходный код с целью упрощения программирования операций с матрицами.

Класс позволяет использовать при программировании переопределенные операции: присвоение, сложение матриц, умножение матриц, умножение матрицы на число (справа). Например, код C++, использующий объекты данного класса, может выглядеть так:

A = B;

A = B + C;

A = B * C;

A = B * c;

где A, B и C – объекты класса, с – переменная типа float, double или long double.

Кроме того, класс содержит функции обращения матрицы, вычисления определителя и транспонирования:

A = B. Inverse(); - обращение матрицы B;

d = B. det(); - вычисление определителя матрицы B;

A = B. T(); - транспонирование матрицы B.

Значения ячеек матрицы имеют тип long double, что позволяет производить операции с большой точностью. В некоторых достаточно сложных прикладных задачах, построенных на итеративных алгоритмах, увеличение точности вычислений приводит к ускорению сходимости алгоритма, то есть даже ускоряет работу программы.

Важное преимущество нашего класса заключается в реализации подхода «динамическая матрица».

В прикладных задачах, связанных с обработкой потоков информации, встает задача оперативного формирования матриц на основе данных (сигналов), поступающих по нескольким каналам. При этом, во-первых, данные не должны пропадать из-за нехватки времени, они должны без временных задержек наполнять матрицы, позволяя математическому алгоритму быстро приступать к их обработке. Во-вторых, память компьютера должна использоваться рационально, чтобы избежать переполнения памяти при больших потоках информации.

Объект класса DMatrix можно изобразить в виде стакана:

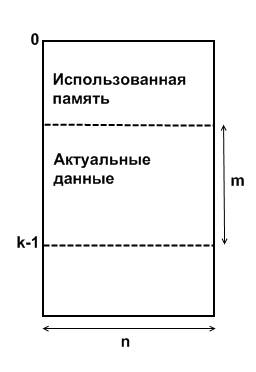
Матрица, хранящаяся в данном объекте, имеет размерность m*n. Как правило, в случае работы с потоком данных число n – это количество переменных, содержащихся в потоке, и/или каких-то рассчитанных величин, например, производных по времени от переменных потока.

Рациональное использование памяти при работе с динамической матрицей подразумевает динамическое выделение памяти для строк матрицы (низ стакана) и динамическое освобождение памяти от использованных строк (верх стакана).

При операциях с матрицами, таких, как сложение, умножение, вычисление определителя и др., обработке подвергаются только актуальные данные, для указания на которые служит переменная k.

При обработке сигналов от устройств часто возникают задача формирования и решения в реальном времени систем уравнений. Для этой цели сделаны классы LSM и PROJECTION, работающие с нашими динамическими матрицами. В них реализованы алгоритмы решения систем линейных алгебраических уравнений с гибкой системой настройки параметров. Алгоритмы базируются на методе наименьших квадратов с «коэффициентом экспоненциального забывания» и проекционном решающем алгоритме. Настройки этих алгоритмов позволяют адаптировать их как для чистки входящих сигналов, так и для быстрого реагирования решения на скачки сигналов на входе. Таким образом, программист (или эксплуатант), подбирая эти настройки, должен найти оптимальный баланс между точностью решения и быстротой реагирования.

Переменные и функции класса DMatrix

Класс содержит переменные:

int m; - количество строк матрицы

int n; - количество столбцов матрицы

int k; - указатель на последнюю строку матрицы. При операциях в качестве актуальных строк матрицы используются строки массива с индексами (k-m), … , (k-1).

int M; - количество указателей на строки матрицы

long double **data; - указатель на двумерный массив значений ячеек матрицы

bool oblom; - признак аварийного результата выполнения операции

Класс содержит функции:

long double __fastcall det(void); - расчет определителя матрицы

DMatrix __fastcall T(void); - транспонирование матрицы

DMatrix __fastcall Inverse(void); - расчет обратной матрицы

void __fastcall Ini(m0, n0, M0, k0); - инициализация переменных объекта-матрицы и выделение памяти

void __fastcall de_allocate(void); - чистка памяти: удаление m строк матрицы из диапазона (k-m), … , (k-1) и указателей на эти строки

void __fastcall Allocate(int k0); - выделение памяти для указанной строки

void __fastcall Delete(int k0); - чистка памяти: удаление указанной строки

Работа с матрицами

Пример 1.

Рассмотрим простейший пример – сложение двух матриц:

+

Сначала нужно добавить в проект наш класс. Если используется среда Borland Builder, то необходимо добавить в проект файл dmatrix.cpp и подключить его в unit’е, в котором мы будем работать с матрицами; для этого напишем в header-файле директиву #include "dmatrix.h".

Добавим на форму кнопку Button1 и надпись Label1. В функцию Button1Click поместим следующий код.

Объявим 3 матрицы:

DMatrix A, B, C; (слагаемые и результат, C = A + B),

опишем свойства этих матриц и выделим память для строк и столбцов матриц:

A.m = 2;

A.n = 2;

A.k = 2;

A.M = 2;

A.oblom = false;

A.data = new long double*[A.M];

for (int i = 0; i < A.k; i++) A.data[i] = new long double[A.n];

То же самое можно написать более компактным образом, с помощью функции Ini:

A.Ini(2, 2, 2, 2);

В результате выполнения функции Ini(m0, n0, M0, k0) задаются значения переменных A.m, A.n, A.M, A.k, выделяется память для A.M указателей на строки и выделяется память для A.k строк.

Примечание по работе Ini:

Иногда нет смысла сразу выделять память под строки. В этом случае можно написать: A.Ini(2, 2, 2). После выполнения функции Ini с тремя аргументами будет присвоено A.k = 0, о чем не стоит забывать, т.к. A.k = 0 указывает на матрицу из 0 строк; если мы хотим указать на матрицу из A.m строк, то A.k должен быть не меньше A.m.

Можно также сделать двухместный вызов этой функции: A.Ini(2, 2), в этом случае не будет выделена память для указателей на строки и будет присвоено A.M = 0.

Так же поступим с матрицами B и C:

B.Ini(2, 2, 2, 2);

C.Ini(2, 2, 2, 2);

Зададим значения ячеек матриц A и B:

A.data[0][0] = 1;

A.data[0][1] = 2;

A.data[1][0] = 3;

A.data[1][1] = 4;

B.data[0][0] = 5;

B.data[0][1] = 6;

B.data[1][0] = 7;

B.data[1][1] = 8;

и, наконец, сложим матрицы:

C = A + B;

В результате сложения в массиве C.data появится требуемый результат, который можно вывести на экран. Например:

Label1->Caption = FloatToStr(C.data[0][0]); - на форме отобразится значение ячейки (1-я строка, 1-й столбец), равное 6.

После получения результата и его выгрузки освободим память:

if(A.data) A.de_allocate();

if(B.data) B.de_allocate();

if(C.data) C.de_allocate();

Важное замечание по поводу работы функции de_allocate(): эта функция удаляет только строки в диапазоне (k-m), … , (k-1) (имеются в виду индексы массива data в C++ коде, то есть нумерация идет с 0). То есть «рабочую» часть нашего стакана. Перед запуском de_allocate() надо быть уверенным, что все прочие строки, лежащие вне данного диапазона, были удалены ранее. В нашем примере k = m, поэтому функцию выполнять можно; вопрос постепенного удаления «отслуживших» строк рассмотрим в следующем примере.

Исходный код рассмотренного примера – здесь.

Пример 2.

Предположим, что требуется оценивать некоторую характеристику потока измерений, поступающих в компьютер с внешних устройств. Например, это данные с N датчиков.

В каждый момент времени имеем N значений, из которых можно составить строку матрицы, то есть можно сказать, что на вход приходят строки. Пусть характеристика, которую надо вычислять – детерминант. Для того, чтобы его вычислить, нам нужно иметь N строк, т.к. матрица должна быть квадратной.

Опишем матрицу и выделим память (только для указателей на строки):

X.Ini(N, N, 10000); // Не указали значение k - не выделилось место под строки

X.k = 1;

Далее в цикле будем симулировать N сигналов и обрабатывать их:

while(X.k <= X.M)

{

X.Allocate(X.k - 1); // Выделяем память для строки

if(X.k > X.m) X.Delete(X.k - X.m - 1); // Удаляем последнюю использованную, но пока не удаленную строку

// Заполняем новую строку (симуляция сигналов)

for(i = 0; i < N; i++)

X.data[X.k - 1][i] = (((rand() % RAND_MAX)+1.0)/RAND_MAX); // Равномерно распределенная на [0,1] случайная величина

if(X.k >= X.m) det = X.det(); // Появилось m строк - можно считать определитель

X.k++;

}

Полный текст программы - здесь. В исходном коде добавлено умножение матрицы на себя, дискриминант берется от матрицы-произведения. Отображение результатов на форме сделано с помощью таймера.

Исходя из значения X.M можно оценить, сколько раз в секунду Ваш компьютер находит значение определителя матрицы размера N*N (всего определитель вычисляется (X.M-N+1) раз). Увеличивая размер матрицы, можно получить представление о возможностях алгоритма.

Важное замечание: в этом примере мы освобождали и выделяли память для строк на каждом шаге. Для повышения быстродействия иногда имеет смысл перераспределять память с интервалом в несколько шагов, большими кусками. То есть через несколько шагов добавлять / удалять сразу по несколько строк матрицы.

Так как функция de_allocate() освобождает память от строк с индексами из диапазона (k-m), … , (k-1), важно перед запуском функции указать правильное значение k. Для этого в исходном коде после главного цикла указано: X.k--; , чтобы сбросить последнее увеличение X.k на единицу.

Динамическая идентификация состояния системы

Для демонстрации возможностей работы с классом предлагается пример (с исходниками).

При запуске программы (matrix.exe) открывается форма, на которой можно задавать матрицы и производить простейшие операции с ними. В исходном тексте можно увидеть, каким образом используется наш класс при программировании на C++.

При нажатии на кнопку «Динамические операции» открывается форма для решения следующей задачи.

Пусть у нас есть 4 сигнала, поступающих на вход: X₁, X₂, X₃ и Y. Мы предполагаем, что эти 4 переменные связаны между собой линейным уравнением:

C₁ * X₁ + C₂ * X₂ + C₃ * X₃ = Y

В качестве одного или нескольких входных параметров может использоваться как физический сигнал, так и расчетные величины, например, производные или отфильтрованные данные.

Требуется оценить в каждый момент времени коэффициенты состояния системы C₁, C₂, C₃, то есть решить уравнение относительно C_i.

В идеальных условиях, при отсутствии шума и при постоянных X₁, X₂, X₃ и Y в каждый момент времени мы получаем одно и то же уравнение, имеющее бесконечное множество решений. На практике мы имеем шум и изменяющиеся значения сигналов, в результате чего получается система из большого количества несовместных уравнений.

Для приближенного решения несовместной системы существует несколько вычислительных подходов; в нашей программе реализована комбинация 2-х методов: МНК (Метод наименьших квадратов) с «коэффициентом экспоненциального забывания» и обобщенный проекционный алгоритм.

Использование подхода МНК обусловлено необходимостью получения на каждом шаге невырожденной матрицы для последующего решения системы уравнений проекционным алгоритмом. Для увеличения гибкости настройки вводится коэффициент экспоненциального забывания W², смысл которого состоит в усреднении вновь полученной методом МНК системы с аналогичной системой, полученной на предыдущем шаге. Чем больше значение W², тем больший вес имеют предыдущие значения. Коэффициент принадлежит интервалу [0, 1).

Проекционный алгоритм работает методом пошагового уточнения решения, то есть на каждом шаге на вход алгоритма подается 1 уравнение. Каждое из этих уравнений есть очередные строка и значение свободного члена, которые последовательно поставляются из системы – результата применения МНК. В качестве стартового решения, то есть вектора C, берется произвольный набор чисел (в программе – 1, 2, 3, 4, 5, ...).

Подробнее ознакомиться с модифицированным МНК и обобщенным проекционным алгоритмом можно в этой статье.

Рассмотрим настройки параметров сигнала и алгоритмов.

Панель «Заданные параметры модели» предназначена для задания коэффициентов C₁, C₂, C₃. Так как реального сигнала на входе у нас нет, мы должны его симулировать, причем переменная Y должна рассчитываться на основе априорного знания параметров объекта C₁, C₂, C₃, которые в дальнейшем рассчитываются с помощью наших решающих алгоритмов.

На панели «Сигнал на входе» задаем средние значения (EX_i) и дисперсии (DX_i) для X₁, X₂, X₃. Эти сигналы моделируются как нормально распределенные случайные величины. Сигнал Y рассчитывается по X₁, X₂, X₃ и C₁, C₂, C₃ с помощью линейного уравнения с рандомизацией. В реальных условиях всегда присутствует шум, поэтому добавляем его следующим образом: рассчитанное по уравнению значение принимаем за мат. ожидание Y, дисперсию Y задаем с формы. В результате такой рандомизации получаем несовместные уравнения.

Задаем параметры МНК. «Шаг формирования МНК» показывает, через сколько единиц времени будет формироваться новая квадратная система уравнений по МНК. «Блок МНК» - количество уравнений, из которых формируется такая система уравнений. Шаг формирования МНК не может быть больше толщины блока, то есть мы формируем МНК из большого количества уравнений и достаточно часто. «W2» - коэффициент забывания.

Параметры проекционного алгоритма служат для «перезагрузки» внутренней информации алгоритма при возникновении большой степени линейной зависимости уравнений. Правильный подбор этих параметров позволяет избежать «выпрыгивания» решения из пространства разумных решений в «фантастические» и, в то же время, обеспечить необходимую точность решения.

Для начала не будем ничего менять, просто нажмем кнопку «Расчет». Синей линией обозначены значения наперед заданных C_i, красной – значения рассчитанных C_i. По мере накопления информации алгоритм улучшает решение.

Сбросим дисперсию Y нажатием на кнопку «-». Через некоторое время значения начнут определяться практически точно, с точностью до вычислительной погрешности.

Изменим заданное значение одного из C_i нажатием на «+100%» или «-100%». Через некоторое время алгоритм найдет новое решение.

Для того, чтобы увеличить адаптивность алгоритма, уменьшим количество строк матрицы МНК (нажать несколько раз «-10%» рядом с параметром «Блок МНК») и еще раз изменим заданное значение одного из C_i. Алгоритм найдет новое решение гораздо быстрее. Из-за того, что графики масштабируются автоматически, может показаться, что точность увеличилась; на самом деле, она уменьшилась с уменьшением количества строк.

Приемы работы с графиками:

1. Нажать левую кнопку мыши, провести мышью слева направо + сверху вниз и отпустить кнопку. Выделенный таким образом фрагмент будет увеличен.

2. Нажать правую кнопку мыши, передвинуть мышь и отпустить кнопку. Таким способом график будет передвинут.

3. Нажать левую кнопку мыши, провести мышью справа налево + снизу вверх и отпустить кнопку. Положение и масштаб графика будут восстановлены до рассчитанных автоматически.

Частота в герцах, отображаемая рядом с кнопкой «СТОП», показывает, сколько раз в секунду наш алгоритм находит решение (на форму решения выдаются с частотой 2Гц). При установках по умолчанию мы имеем на входе МНК матрицу размером 10000 * 3, которая на каждом шаге формирования МНК преобразуется в матрицу 3 * 3. Проекционный алгоритм также включает в себя большое количество матричных операций, см. функцию Go() в классе PROJECTION. Таким образом, Вы можете оценить эффективность предложенной схемы.

Теперь поиграем с параметрами проекционного алгоритма.

Параметры Z2F и SMAX задают уровень отсечки решений из «фантастической» области. Установим Z2F = 1E-23 и запустим расчет. Время от времени решения будут проваливаться в «фантастическую» область. Теперь поставим SMAX = 2. Провалы прекратятся.

Параметр Z2F определяет недопустимый уровень линейной зависимости; SMAX контролирует то же самое, но более грубо, по количеству итераций при обработке проекционным алгоритмом нового уравнения.

Итак, возможны две крайности.

1. Обрабатываемый сигнал может иметь стабильные или медленно изменяющиеся мат. ожидания. В этом случае можно усилить некоторые параметры алгоритма с целью увеличения точности решения.

2. Сигнал может быстро изменяться. Тогда имеет смысл подбирать параметры так, чтобы решения адаптировались как можно быстрее.

	Шаг МНК	Блок МНК	W2
Сигнал стабильный	Уменьшить	Увеличить	Увеличить
Сигнал изменчивый	Увеличить	Уменьшить	Уменьшить

Переменные и функции классов LSM и PROJECTION

Класс LSM содержит переменные:

DMatrix A_buf, b_buf; - МНК-матрица и МНК-столбец, в которых формируется результат

(по формулам A_buf = A^TA и b_buf = A^Tb)

DMatrix Stolbets, Matritsa1, Matritsa2; - буферные матрицы, используемые для проведения

вычислений по этим формулам

int frstLSM; - признак того, что МНК-матрица и МНК-столбец

рассчитываются впервые

Класс LSM содержит функции:

bool __fastcall Ini(int rows, int cols); - выделение памяти для буферных матриц и

матриц с результатом

void __fastcall Go(DMatrix *A, DMatrix *b, double W2); - формирование результата на основе

исходных матрицы и столбца (используется указатель на них) и коэффициента W2

void __fastcall Del(void); - очистка памяти от данных буферных матриц и

матриц с результатом.

Класс PROJECTION содержит переменные:

DMatrix X; - вектор входных переменных

DMatrix C; - вектор результата

DMatrix A, Z, BS, Matritsa, Stroka, Stolbets, Chislo; - матрицы, используемые для вычислений

long double y, dy, Z2, dbuf; - переменные, используемые для вычислений

int SMAX, k, S; - переменные, используемые для вычислений

int Superior, AIsE; - переменные, используемые для вычислений

Класс PROJECTION содержит функции:

bool __fastcall Ini0(int cols); - выделение памяти для буферных матриц и вектора результата

void __fastcall Ini1(void); - сброс матрицы A и счетчика S при недопустимой степени

линейной зависимости

int __fastcall Go(DMatrix *X0, DMatrix *Y0, int SMAX, double Z2F); - тело алгоритма

void __fastcall Del(void); - очистка памяти

Преимущества DMatrix

Данные, последовательно поступающие на обработку с помощью объектов нашего класса, располагаются в памяти, занимая последовательно выделяемые для них адреса.

Возникает вопрос, чем это лучше, чем «обычный» способ? А именно, почему бы не выделить раз и навсегда память под матрицу нужного размера? Имея матрицу фиксированного размера, можно в каждый момент времени сдвигать строки в ней, стирая старейшую строку и добавляя новую.

У нашего способа есть ряд преимуществ перед таким «обычным» способом:

1. Не надо делать сдвиги всех строк; расположение информации по ячейкам массива происходит «раз и навсегда», что облегчает написание кода программистом и экономит время.

2. Можно хранить историю; например чтобы анализировать данные на разных временных масштабах, используя для экономии памяти стирание содержимого строк (то есть делать прореживание).

3. Можно динамически-автоматически менять m – актуальную толщину матрицы. Например, при резких изменениях данных логично толщину уменьшать, при стабилизации – увеличивать. Так как мы, вообще говоря, не знаем, на сколько строк может быть увеличена толщина матрицы, логично хранить все строки. На практике хранение всех строк может привести к переполнению памяти, поэтому разумно, все же, вводить некую константу mMax (m ≤ mMax), при достижении которой стираются старые строки. Но так как эта константа достаточно велика, до ее достижения проходит много времени, скажем, несколько минут, в течение которых сохраняются все данные и идет выдача результатов расчетов.

Обновление от 18.04.2018.

Операции с объектами класса DMatrix используют объекты temp и E, описанные в файле dmatrix.cpp как глобальные переменные. Это приводило к ошибке при создании объектов DMatrix в нескольких процессах (Thread) одного приложения, т.к. temp и E имели одни и те же адреса в разных процессах.

Поэтому эти объекты теперь описываются как массивы: DMatrix temp[10], E[10]; .

Теперь при использовании объектов DMatrix в разных процессах после вызова функции Ini надо указывать номер процесса:

DMatrix X;

X.Ini(…, …, …, …);

X.Thr = [номер процесса (от 0 до 9)];

Если процесс – единственный, этого делать не надо, по умолчанию Thr = 0.

То же касается и инициализации объектов LSM и PROJECTION. В этих классах в функциях инициализации добавлена еще одна переменная (по умолчанию также равная 0):

LSM Lsm;

Lsm.Ini(…, …, [номер процесса]);

PROJECTION Projection;

Projection.Ini0(…, [номер процесса]);

Все исходники, доступные к скачиванию с данной страницы, обновлены с учетом этих изменений.

Спросить на форуме