Технический перевод

Операции с матрицами: программирование на C++

Главная

6.4 Рамы на двух опорах с промежуточным шарниром

Как отмечалось выше, рамы на двух шарнирно-неподвижных опорах с одним промежуточным шарниром также являются статически определимыми.

Пример 4. Рассмотрим построение эпюр  для рамы с  промежуточным шарниром (рис.6.5,а)

В дополнение к условиям равновесия, рассмотренным в примерах 3 и 4, здесь для определения неизвестных реакций  используются еще два условия:  и  , каждое из которых по своей сути выражает факт равенства нулю изгибающего момента  в промежуточном шарнире С (рис.6.5,а).

Для определения четырех неизвестных реакций возможно использование различных комбинаций уравнений равновесия, но чаще всего используются следующие уравнения:

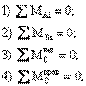
При этом для проверки вычисленных реакций служат уравнения:

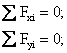
При заданных нагрузках (рис.6.5,а) уравнения равновесия принимают вид:

Знак "-", полученный при вычислении реакции , говорит о необходимости изменить принятое для нее направление на противоположное (перечеркнутая стрелка на рис.6.5,а).

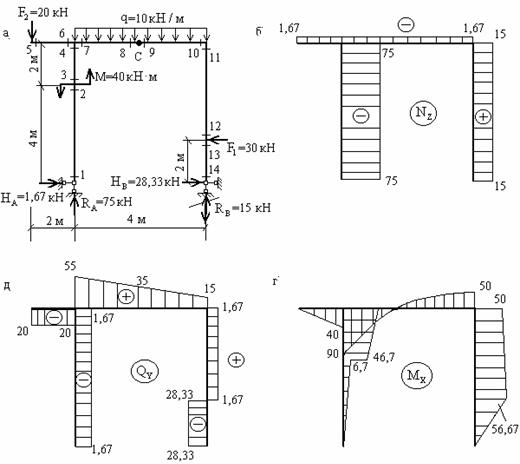
Рис 6.5

Проверяем правильность вычисления опорных реакций.

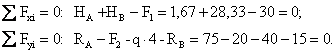
Теперь вычисляем значения  в характерных сечениях, выбирая для сечений 1-8 левую отсеченную часть, а для сечений 9-14 - правую.

Из рассмотрения левой отсеченной части:

(сжаты правые волокна стойки);

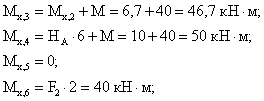
(сжаты нижние волокна ригеля);

Вновь подчеркнем, что знаки "+" и "-" для изгибающих моментов  принимаются относительно, то есть для разграничения противоположно направленных моментов, а эпюра  строится со стороны сжатых волокон.

Из рассмотрения правой отсеченной части:

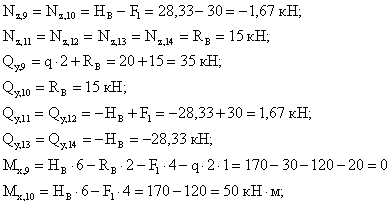
(сжаты верхние волокна ригеля)

(сжаты правые волокна стойки)

Эпюры , построенные по вычисленным значениям, приведены на рис.6.5,б,в,г.