Технический перевод

Операции с матрицами: программирование на C++

Главная

6.3. Рамы на двух шарнирных опорах

В дальнейшем для краткости будем говорить "шарнирная рама", имея в виду ее статическую определимость и отсутствие промежуточных шарниров.

Пример 2. Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере, но с шарнирным опиранием (рис.6.3,а).

Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией.

Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:

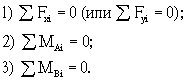
Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию.

Так, в рассматриваемом примере этим условием будет = 0, которое будет содержать неизвестную реакцию H_A (в то время как условие = 0 содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие = 0.

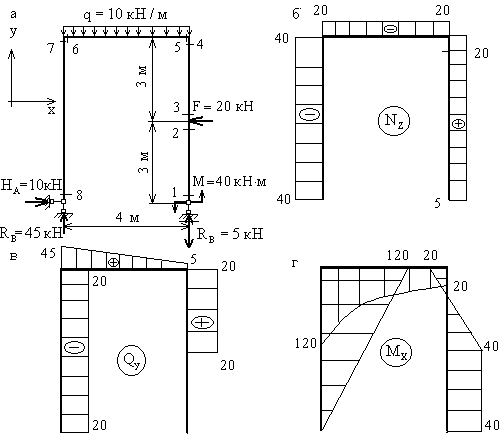
Рис. 6.3

Второе и третье уравнения равновесия (= 0, = 0) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения (иногда - с нулевым плечом).

В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть = 0 или =0.

Построение эпюр N_z, Q_y и M_x в шарнирных рамах выполняется так же, как и в защемленных, но " с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.

Вычислим реакции опор рамы (рис.6.3,а)

Уравнения статики:

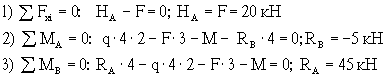
Знак "-", полученный при вычислении реакции R_A, говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:

,

то есть реакции опор вычислены правильно.

Построение эпюры N_z.

Двигаясь по оси рамы от сечения 1 к сечению 6, получим:

N_z,1 = N_z,2 = N_z,3 = N_z,4 = R_B = 5 кН,

N_z,5 = N_z,6 = - F = - 45 кН.

Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:

N_z,8 = N_z,7 = - R_A = - 45 кН.

Этот же результат получим из рассмотрения отсеченной части 1-6:

N_z,7 = N_z,8 = - R_B - q·4 = - 45 кН.

По вычисленным значениям строим эпюру N_z (рис.6.3,б)

Построение эпюры Q_y.

Из рассмотрения отсеченной части 1-5:

Q_y,1 = Q_y,2 = 0,

Q_y,3 = Q_y,4 = F = 20 кН,

Q_y,1 = R_A = 5 кН.

Из рассмотрения отсеченной части 8-6:

Q_y,8 = Q_y,7 = - H_A = - 20 кН,

Q_y,1 = R_A = 45 кН.

Эпюра Q_y, построенная по вычисленным значениям, показана на рис.6.3,в.

Построение эпюры M_x.

Из рассмотрения отсеченной части 1-5:

M_x,1 = M_x,2 = M = 40 кН·м (сжаты правые волокна стойки);

M_x,3 = M_x,2 = 40 кН·м (плечо силы F равно нулю);

M_x,4 = M_x,5 = M - F·3 = - 20 кН·м (сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);

Из рассмотрения отсеченной части 8 -6:

M_x,8 = 0,

M_x,7 = M_x,6 = H_A·6 = 120 кН·м

(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно).

Эпюра M_x показана на рис.3,г.

Пример 3. Рассмотрим шарнирную раму более сложной конфигурации (рис.6.4,а).

Здесь необходимо рассматривать 10 характерных сечений для построения эпюр N_z, Q_y и M_x. Сечения 1-6 расположены на ригеле слева направо, а сечения 7-10 - на стойке сверху вниз. Как и в предыдущем примере, указанное расположение характерных сечений является безусловно необходимым, а их нумерация - произвольной.

Уравнения статики для вычисления опорных реакций имеют вид:

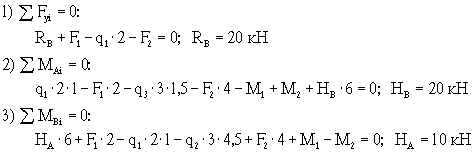
Проверка вычисления опорных реакций:

При построении эпюр N_z, Q_y и M_x целесообразно выбирать отсеченную часть, продвигаясь к центральному узлу рамы с четырех сторон, т.к. в этом случае определение внутренних силовых факторов в каждом из характерных сечений осуществляется наиболее просто.

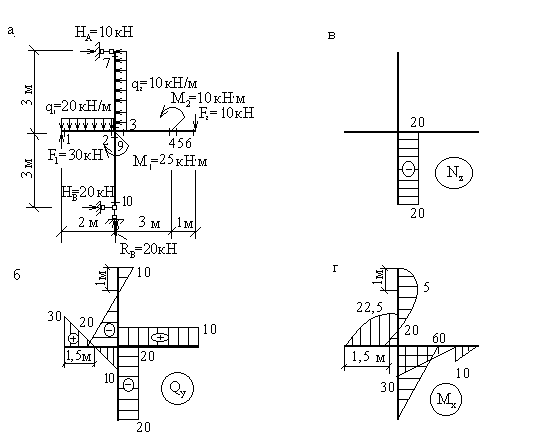
Рис.6.4

Построение эпюр N_z, Q_y и M_x .

Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):

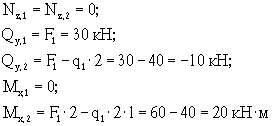 (сжаты верхние волокна).

Из рассмотрения правой отсеченной части (сечения 3-6):

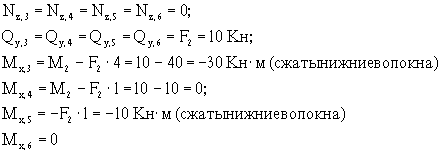
Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):

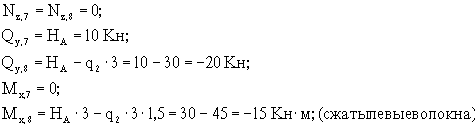
Из рассмотрения нижней отсеченной части (сечения 9-10):

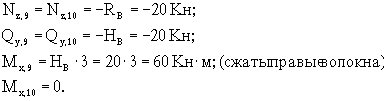
Характер эпюры Q_y на участках рамы с распределенными нагрузками q₁ и q₂, а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент M_x принимает экстремальные значения. Определение положений точек пересечения (т.е. тех точек, где Q_y = 0) выполняется так же, как и в балках.

Вычислим экстремальные значения момента M_x.

На участках под распределенной нагрузкой q₁:

 (сжаты верхние волокна).

На участке с распределенной нагрузкой q₂:

 (сжаты правые волокна).

Эпюры N_z, Q_y и M_x показаны на рис.6.4,б,в,г.