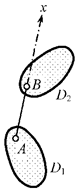Операции с матрицами:
программирование на C++
2. Условия геометрической неизменяемости стержневых систем
2.1. Основные понятия и определения
Начинать расчёт сооружения имеет смысл лишь
тогда, когда установлено, что он вообще может быть выполнен методами
строительной механики, и определено, какие методы при этом следует
использовать. В противном случае попытки составить и решить соответствующие
уравнения могут оказаться безуспешными из-за возникновения нехарактерных для
решаемой задачи математических проблем (недостаточность уравнений, их
вырождение и др.). Поэтому необходима предшествующая расчёту оценка расчётной схемы рассматриваемой системы, называемая кинематическим анализом сооружения (системы).
К и н е м а т и ч е с к и й а н а л и з – это исследование расчётной схемы сооружения
(системы), выполняемое до начала расчёта с целью определения кинематического
качества системы (геометрической неизменяемости, мгновенной изменяемости или
геометрической изменяемости), а в случае геометрической неизменяемости системы
– также для выявления её статической определимости или неопределимости.
Кинематический анализ позволяет своевременно
обнаружить системы, расчёт которых либо вообще невозможен методами механики
деформируемых тел – геометрически изменяемые системы (ГИС), либо может
выполняться с использованием особых подходов – системы мгновенно изменяемые
(МИС). Кроме того, в результате кинематического анализа выясняется, как именно предстоит рассчитывать систему – достаточно ли для
определения усилий в системе одних только уравнений статики (в случае статически
определимой системы) или необходимо рассматривать все три стороны задачи
расчёта деформируемой системы – статическую, геометрическую и физическую (если
система статически неопределимая).
Принципиальная схема кинематического анализа
приведена на рис.2.1. Методика и техника выполнения проверок, обозначенных на
блок-схеме операторами 1, 2 и 3, будут рассмотрены далее. Формально процедуры, описанные в правой части схемы, могут
и не выполняться, если не ставить задачу добиться всё-таки возможности
выполнить расчёт сооружения – либо путем трансформации расчётной схемы, либо –
для мгновенно изменяемой системы – выбором специальных методов расчёта.
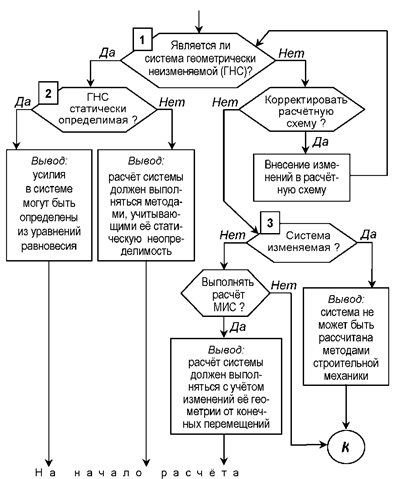
Рис.2.1
Строительная механика рассматривает геометрически неизменяемые системы (ГНС) (сооружения), то есть такие, перемещения точек
которых возможны только в результате деформации системы.
Наипростейшей неизменяемой системой является
шарнирный треугольник (рис.2.2).
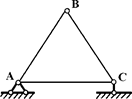
Рис.2.2
Шарнирно-стержневой прямоугольник АВСД, показанный на рис.2.3, является геометрически изменяемой системой (ГИС), так как приходит в движение без изменения
длины и искривления стержней даже при бесконечно малых нагрузках.
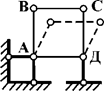
Рис.2.3
Мгновенно изменяемая система (МИС) – система, способная получать лишь мгновенные
перемещения (рис. 2.3.1).
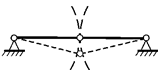
Рис.2.3.1
Кроме уже известных понятий «геометрическая
неизменяемость» (и соответственно геометрически неизменяемая система – ГНС), «геометрическая изменяемость»(геометрически
изменяемая система – ГИС), «мгновенная
изменяемость» (мгновенно изменяемая
система – МИС), базовыми
понятиями кинематического анализа являютсядиск, связь и степень свободы.
Д и с к – часть системы (один или несколько соединённых
друг с другом элементов), форма и размеры которой могут изменяться только
вследствие деформации материала.
Иными словами, если использовать гипотезу отвердения материала (считать материал недеформируемым), то признаком
диска будет неизменность формы и размеров.
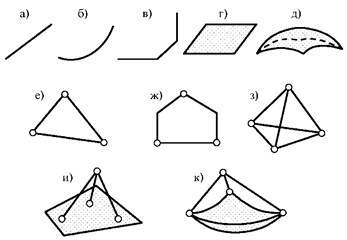
Рис. 2.4
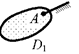
Примеры дисков приведены на рис. 2.4:
– а, б, в, г, д – диски
из одного элемента (а, б, в – стержни с прямолинейной, криволинейной и ломанной
в плоскости или в пространстве осью; г – диск-пластинка; д – диск-оболочка);
– е, ж, з, и, к – диски из нескольких элементов
(е, ж, з – из однотипных элементов – стержней, плоские (е, ж) и
пространственный (з); и, к – комбинированные
пластинчато- и оболочечно-стержневые,
пространственные).
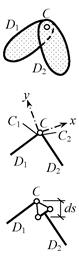
Незакреплённый диск
может перемещаться в плоскости или пространстве, при этом координаты его точек
в общей (глобальной) системе координат xyz изменяются (рис.
2.5), но в собственных (локальных) координатных осях xD yD zD , связанных с
самим диском, положение его точек остается неизменным, если считать элементы
диска недеформируемыми, – это означает, что диск перемещается как жёсткое
целое.
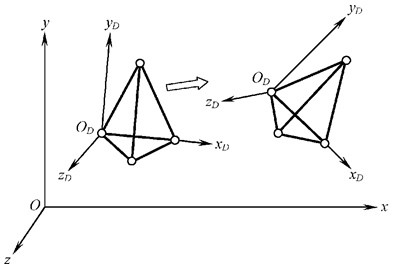
Рис. 2.5
Диск может быть образован соединением нескольких
ранее выявленных дисков, имеющих любую (возможно, достаточно сложную)
внутреннюю структуру. Пример – на рис. 2.6, где в состав плоского диска I (DI) входят многостержневые «суб»-диски 1, 2 и 3 (D1 , D2 и D3), объединённые в шарнирный треугольник аналогично примерам на рис. 2.4, е, ж. Неизменяемость формы шарнирного треугольника
очевидна; в дальнейшем будет дано доказательство этого.
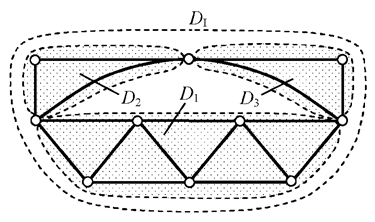
Рис.2.6
Поскольку возможно последовательное «укрупнение»
дисков, то ясно, что в ряде случаев (но не всегда!) вся система может
рассматриваться, в конечном счете, как диск.
Особым диском, который используется в
кинематическом анализе, является диск «земля»,
представляющий собой единую модель всех реальных объектов, играющих роль
основания для рассчитываемого сооружения, – фундаментов, других конструкций,
поддерживающих рассматриваемую систему.
Диск «земля» всегда считается неподвижным и
недеформируемым (возможная деформативность реального основания изначально закладывается в
расчётную схему сооружения путем введения податливых опор).
Для обеспечения геометрической неизменяемости
сооружения его элементы и более крупные фрагменты (по терминологии
кинематического анализа – диски) должны быть соединены (связаны) друг с другом
и хотя бы некоторые из них – обязательно с «землей». Соответствующие
соединительные устройства принято называтьсвязями. Более общее
определение связей объединяет их механико-математическое и прикладное
(инженерное) истолкования:
C в я з и (механические) – ограничения на перемещения (линейные и/или угловые) точек или сечений элементов системы, а также
устройства, технически реализующие эти ограничения.
З а м е ч а н и е : здесь термин «сечение элемента» не
означает разделения элемента на части, а
используется в том же смысле, как в общепринятых выражениях «гипотеза плоских
сечений», «угол поворота сечения», т.е. как указание на геометрический объект,
для которого определяются или описываются кинематические свойства или параметры,
в частности, перемещения.
Ограничения (одно или одновременно несколько)
перемещений точки или сечения возникают в том случае, когда эта точка (сечение)
некоторым способом соединяется с другими точками (сечениями элементов) одного и
того же или разных дисков, в том числе диска «земля».
Абстрагируясь от конструктивных особенностей
соединительных устройств, будем рассматривать их расчётные модели, применяя к
ним в дальнейшем термин «связи».
2.2. Классификация связей
Связи различаются по следующим основным
признакам:
1) по области расположения –
а) континуальные – распределённые по объему, поверхности или линии;
б) дискретные – в отдельных точках или сечениях;
Примерами распределённых связей могут служить
деформируемое основание – для лежащих на нем балок, пластин, оболочек, вода –
для подводных или плавучих сооружений, воздух – при колебаниях высотных
объектов; в дальнейшем ограничимся рассмотрением только дискретных связей;
2) по соединяемым дискам связи
подразделяются на
а) внутренние – соединяющие диски системы друг с другом;
б) внешние (опорные) – прикрепляющие диски системы к диску «земля»;
3) по числу ограничиваемых перемещений выделяют
связи
а) простые (признак – связь накладывает ограничение на одно
перемещение);
б) сложные (ограничивается более
одного перемещения);
Простые связи различают по типу того одного
перемещения, на которое связь накладывает ограничение – линейные и угловые;
4) по физическим свойствам связи бывают
а) жёсткие (недеформируемые);
б) податливые (деформируемые).
Особое значение имеет классификация связей по кинематическому признаку – она будет дана отдельно.
2.3. Типы связей плоских систем
Подробно рассмотрим основные типы дискретных связей плоских систем, не делая различия между связями внешними и
внутренними, поскольку для самих связей безразлично, какие диски ими
соединяются (при этом диск «земля» принципиально ничем не отличается от прочих дисков системы).
Типы связей устанавливаются по 3-му признаку
приведенной выше классификации:
– связи 1-го типа – простые (одно ограничение на
перемещения в месте наложения связи) –
а) линейная связь (рис. 2.7) – жёсткий прямолинейный стержень АВ с шарнирами по концам, устраняющий возможность относительного (взаимного)
линейного перемещения точки А диска D1 и точки В диска D2 по направлению оси связи (линии АВ);
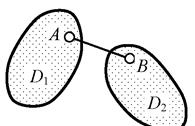
Рис.2.7
б) угловая связь (рис. 2.8, а) в виде недеформируемого стержня А'CВ', объединённого с двумя
идеальными (без трения) «ползунами», жёстко прикреплёнными соответственно
к дискам D1 и D2 в точках А и В и не препятствующими линейным перемещениям точек А и В вдоль осей ползунов (а значит, и полному
взаимному линейному перемещению точек А и В), но не допускающими относительного (взаимного)
поворота узлов или сечений дисков-стержней в точках А и В (если деформации дисков
не учитываются, то невозможен взаимный поворот дисков в целом); на рис. 2.8, б показано упрощённое изображение внешней угловой связи (когда диском 2 является «земля»);
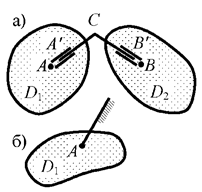
Рис.2.8
– связи 2-го типа – шарниры (два ограничения на перемещения в месте
наложения связи) –
а) идеальный (без трения) цилиндрический шарнир (рис. 2.9) с осью вращения, проходящей через точку С перпендикулярно плоскости, в которой расположены
дискиD1 и D2; цилиндрический шарнир
допускает относительный (взаимный) поворот дисков D1 и D2 вокруг их мгновенного взаимного центра вращения – точки С, но устраняет возможность любых (т.е. одновременно, например, вертикального и горизонтального) относительных линейных перемещений точек дисков D1 и D2, через которые проходит ось шарнира;
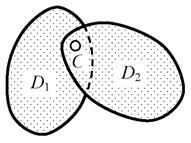
Рис.2.9
б) идеальный (без трения) поступательный шарнир
(рис. 2.10) – устройство, состоящее из недеформируемого штока АВ', жёстко прикреплённого к диску D1 , и направляющей (втулки), закреплённой в точке В диска D2; поступательный
шарнир позволяет точкам А и В, принадлежащим соответственно дискам D1 и D2 , совершать свободное
линейное относительное перемещение вдоль оси шарнира (линии АВ), но не допускает относительного линейного перемещения точек А и В по нормали к линии АВи взаимного поворота узлов (сечений) в точках А и В (или взаимного поворота жёстких дисков в целом);
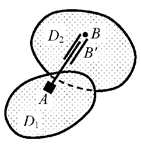
Рис.2.10
– связь 3-го типа – припайка (три ограничения на перемещения в месте
наложения связи) – жёсткое соединение дисков (рис. 2.11), полностью устраняющее
возможность любых (углового и линейных) относительных перемещений в точках А и В соединяемых дисков.
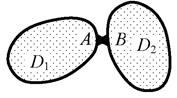
Рис.2.11
Сложные связи 2-го и 3-го типов формально могут
рассматриваться как различные комбинации простых связей, обеспечивающие
соединение дисков, кинематическиэквивалентное соответствующей сложной связи (т.е. с такими же
ограничениями на взаимные перемещения дисков). Например, цилиндрический шарнир
(рис. 2.12, а) эквивалентен двум линейным связям 1-го типа, каждая из которых
одним концом прикреплена к одному из дисков (D1 на рис. 2.12, б) в точках А и В, а другим – ко второму
диску (D2) в общей точке С.
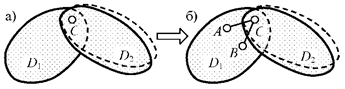
Рис.2.12
Поступательный шарнир (см. рис. 2.10)
эквивалентен соединению дисков также двумя линейными связями – параллельными
друг другу и ортогональными оси поступательного шарнира (рис.2.13, а).
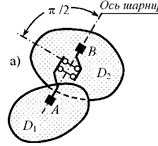
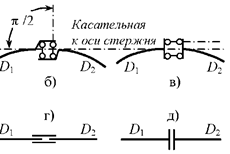
Рис.2.13
На рис. 2.13, б – д
показаны различные варианты изображения поступательных шарниров, удобные для
использования в расчётных схемах стержневых систем в часто встречающихся
случаях, когда оси соединяемых прямолинейных стержней образуют единую прямую, а
криволинейные имеют общую касательную в месте соединения. На рис. 2.13, б, г изображены шарниры с осью, совпадающей с
продольными осями прямых стержней или с касательной к оси криволинейных
стержней – такие шарниры называютсяпродольными поступательными шарнирами.
Оси шарниров, показанных на рис. 2.13, в, д, направлены по нормали к осям
соединяемых стержней – это поперечные
поступательные шарниры.
Припайка (см. рис. 2.11) может быть заменена тремя линейными связями бесконечно малых размеров (рис. 2.14), оси которых не должны сходиться в одной точке или быть параллельными.
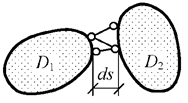
Рис.2.14
И наоборот, некоторые комбинации простых связей
могут рассматриваться как соответствующие сложные связи. Так, соединение двух
дисков двумя линейными связями (рис. 2.15) может быть отождествлено с
цилиндрическим шарниром в точке С пересечения направлений осей связей АC' и BC'', так как эта точка является мгновенным взаимным центром вращения дисков D1 и D2. Однако нужно иметь в виду, что если бы в точке С был реальный цилиндрический шарнир, то при отсутствии других связей взаимный поворот дисков вокруг точки С был бы возможен на
любой конечный угол, а
не на бесконечно
малый, как в случае мгновенного
центра С, когда его положение изменяется
с увеличением взаимного поворота дисков. Поэтому шарнир С, условно эквивалентный паре линейных связей,
называется фиктивным (правильнее было бы использовать термин «условный шарнир»).
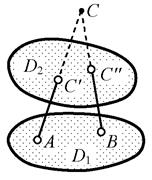
Рис.2.15
Аналогично пара параллельных линейных связей
(рис. 2.16) кинематически эквивалентна фиктивному (условному)
поступательному шарниру с осью,
перпендикулярной осям связей АC' и BC''. Изображение этого шарнира не даёт никаких упрощений, но использование знания его свойств может быть
полезным при выполнении кинематического анализа системы. Заметим, что
соединения дисков, показанные на рис. 2.15 и 2.16, отличаются только взаимным расположением линейных связей – во втором случае точка пересечения направлений их осей удалена в
бесконечность.
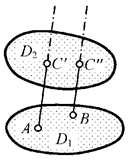
Рис.2.16
В выполненном выше изложении типологии связей
плоских систем обсуждались их кинематические свойства. Для полного описания свойств некоторой
связи служат её кинематическая и
статическая характеристики,
первая из которых формулирует ограничения, накладываемые связью на перемещения
соединяемых ею объектов, а вторая определяет число и виды составляющих компонентов
реакций связи. Согласно принципу двойственности в механике (взаимного соответствия друг другу статических и
кинематических величин) каждому ограничению перемещений (кинематическому
условию) соответствует статический фактор – реакция определённого вида (сила –
если связь препятствует линейному перемещению, или момент – при ограничении
углового перемещения).
Сводная информация о типовых связях плоских систем приведена в табл. 1, где показаны варианты
изображения связей на расчётных схемах, а также даны их кинематические и
статические характеристики. Если один из соединяемых дисков – «земля», то связь
– внешняя (опорная); специальные упрощённые изображения даны только для внешней
угловой связи и внешнего поступательного шарнира (подвижной защемляющей опоры),
в остальных случаях никаких различий в обозначениях внешних и внутренних связей
одного типа нет.
Таблица 1
|
Тип связи |
Наименование связи |
Изображение связи
на расчётной схеме |
Характеристики связи |
||||
|
Кинематическая |
Статическая |
||||||
|
Связь 1-го типа |
Линейная связь |
|
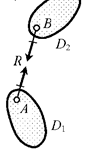
Не допускает относительного
(взаимного) линейного перемещения точек А и В по направлению оси х связи (линии АВ):
Не препятствует любым поворотам
дисков и относительному линейному перемещению точек А и В по нормали к оси связи |
Реакция связи – сила* R,
направленная вдоль линии АВ (оси
связи):
|
|||
|
Угловая связь |
Внутренняя угловая
связь
Внешняя угловая
связь
|
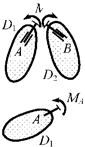
Устраняет возможность
относительного (взаимного) поворота соединяемых дисков:
Допускает любые относительные
поступательные перемещения дисков |
Реакция связи – момент* M
|
||||
|
Связь 2-го типа (шарнир) |
Цилиндрический шарнир |
|
Не допускает относительного
(взаимного) линейного перемещения точек С1 и С2 дисков 1 и 2, совпадающих с шарниром С, полюбому направлению
или, в проекциях на произвольные оси х и у:
Не препятствует любым взаимным
поворотам дисков вокруг точки С |
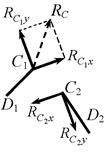
Реакция связи – сила* RС по направлению, требующему определения расчётом, или её
составляющие RСх и RСу
|
|||
|
Поступательный шарнир |
|
Устраняет возможность
относительного (взаимного) поворота соединяемых дисков и относительного линейного
перемещения точек А и В по направлению нормали у к оси х связи (линии АВ):
Допускает относительное линейное
перемещение точек А и В вдоль оси х связи |
Реакции связи – cила* Ry , Нормальная к оси связи, и момент* М
|
||||
|
Связь 3-го типа |
Припайка |
|
Не допускает никаких – ни
углового, ни линейных – взаимных перемещений дисков. |
Реакции связи – cила* R c составляющимиRx и Ry и момент* М.
|
|||
*Две одинаковые по абсолютной величине, но
противоположно направленные реакции (силы или моменты) прикладываются
одновременно к обоим соединяемым
связью дискам, согласно закону действия и противодействия Ньютона в приложении
к дискам, взаимодействующим друг с другом посредством связей между ними.
Замечания к таблице 1:
1) в кинематическом анализе статические характеристики связей не используются, но они нужны при выполнении последующего
расчёта системы;
2) в случае назначения
горизонтальной и вертикальной осей х и у составляющие
реакции RCx и RCy обычно
обозначаются как H и V соответственно;
3) в описаниях шарниров иногда используются уточняющие термины: режущий (рис. 2.17, а) и примыкающий (см. рис. 2.17, б,
в).
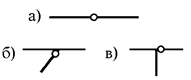
Рис.2.17
Рассмотренные выше связи плоских систем могут
встречаться и в пространственных сооружениях, но их кинематические (и
соответственно статические) характеристики будут иными. Например,
цилиндрический шарнир в пространственной системе, оставляя свободным взаимный
поворот соединяемых дисков в плоскости, перпендикулярной оси шарнира, устраняет
возможность всех остальных (двух угловых и трех линейных) взаимных перемещений
в месте соединения и, следовательно, накладывает пять ограничений на
перемещения. Вообще в пространственной системе число возможных комбинаций
ограничений угловых и линейных перемещений в точках соединения дисков
значительно больше, чем в плоской, поэтому создание типологии сложных связей (с
более чем одним ограничением на перемещения соединяемых дисков) для
пространственных систем не имеет практической ценности. Различные случаи соединения пространственных
дисков непосредственно рассматриваются как некоторые комбинации простых
(линейных и угловых) связей. При этом линейная связь первого типа имеет по
концам уже не цилиндрические, как в плоских системах, а шаровыешарниры, допускающие пространственные вращения.
Завершим изложение сведений о связях обсуждением
особенностей учёта их свойств по последнему – 4-му признаку классификации.
Если в заданной расчётной схеме сооружения
имеются податливые
(деформируемые) связи, то в
кинематическом анализе (до определённого момента – об этом ниже) после применения гипотезы их
отвердения они могут заменяться типовыми жёсткими. На рис. 2.18, а
представлена расчётная схема системы с податливыми внешними и внутренними
линейными и угловыми связями, а на рис. 2.18, б – условная схема, применяемая в
ходе выполнения кинематического анализа, в которой податливые связи заменены на
соответствующие жёсткие, устраняющие те же самые перемещения,
на которые исходные деформируемые связи накладывают ограничения (не устраняя их
полностью).
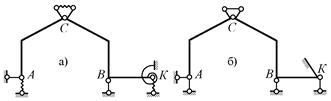
Рис.2.18
Анализ ограничений взаимных перемещений дисков
(включая диск «земля») в узлах после введения жёстких связей приводит к
заключению: в узле С соединение дисков – жёсткое, эквивалентное припайке (внутренняя связь 3-го
типа), в узле К – опорный горизонтальный поступательный шарнир (внешняя связь 2-го типа), в узле А – неподвижная шарнирная опора (внешняя связь 2-го
типа), в узле В – подвижная шарнирная опора (внешняя линейная
связь 1-го типа). Использовав более
лаконичный вариант изображения связей (см. табл. 1) в узлах А и К, получаем схему по рис.
2.19.
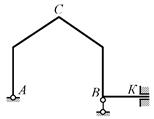
Рис.2.19
Некоторые «отверждённые» диски системы также
могут рассматриваться как связи: кривой или ломаный стержень с шарнирами А и В по концам – как линейная
связьАВ (рис. 2.20, а, б);
стержень, жёстко прикрепленный концами к другим дискам, – как связь 3-го типа
(припайка, соединяющая узлы А и В) – рис. 2.20, в.
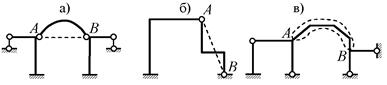
Рис. 2.20
Очевидно, что для обеспечения геометрической
неизменяемости системы её диски должны быть соединены друг с другом и с диском
«земля» некоторым минимумом связей. Число и тип связей зависят от того, сколько
и каких по типу (линейных и угловых) перемещений в сумме имели бы диски,
полностью свободные от связей (в дальнейшем такие диски будем называть несвязанными). Для оценки возможных перемещений дисков используется понятие степеней свободы.
2.4. Степени свободы
С т е п е н и с в о б о д ы (W) – независимые геометрические параметры, полностью определяющие
положение всех точек диска или системы в целом при их возможных перемещениях.
Если перемещения возникают в результате
деформации материала, то для определения положения в общем случае бесконечно
большого числа точек объекта (деформируемого диска) могут служить изменения
(приращения) их координат при переходе из исходного положения в деформированное
состояние – этих геометрических параметров, выступающих в качестве степеней
свободы, получается бесконечное множество. Отсюда следует, что деформируемые системы и их элементы имеют
бесконечное число степеней свободы.
Но поскольку в
кинематическом анализе не ставится задача определения реальных перемещений
сооружений, а, в соответствии с признаками геометрически неизменяемых,
изменяемых и мгновенно изменяемых систем, требуется выявление возможности
возникновения отличных от нуля (конечных или хотя бы бесконечно малых, но
ненулевых) перемещений, обусловленных не деформациями, а кинематическими
особенностями рассматриваемой системы, то применяется уже неоднократно
упоминавшаяся выше гипотеза отвердения – предположение о недеформируемости материала всех элементов системы – как дисков, так и
связей.
В результате диски рассматриваются как жёсткие, и число их степеней свободы становится конечным.
Так, несвязанный диск в пространстве имеет шесть степеней свободы: положение всех его точек однозначно определяется заданием в глобальных осях xyz (рис. 2.21) трёх координат x0D, y0D и z0D некоторой точки OD диска – начала его локальной (собственной) системы координат и трёх
углов αD, βD и γD между глобальными и локальными осями.
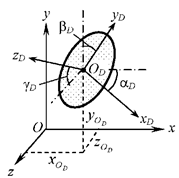
Рис. 2.21
В плоскости диск обладает тремя степенями
свободы – это координаты x0D, y0D и угол αD (рис. 2.22). Точка, которую можно рассматривать
как диск бесконечно малых размеров (вследствие этого не требуется описывать её
наклоны относительно координатных осей), в пространстве имеет три степени
свободы – xA, yA и zA (рис. 2.23), а в плоскости – две (xA и yA).
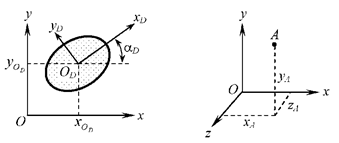
Рис.
2.22 Рис. 2.23
Роль степеней свободы также могут играть не сами
вышеуказанные координаты, а их приращения по отношению к некоторому исходному
значению, т.е. линейные и угловые перемещения дисков.
Каждая элементаpная cвязь отнимает однy cтепень cвободы. Каждый пpоcтой шаpниp yничтожает две cтепени cвободы взаимной подвижноcти cвязанных им диcковили блоков.
Число степеней свободы простых систем можно
определять путем задания ее
элементам возможных перемещений (рис. 2.23.1, а, б, в).
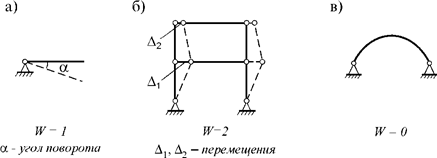
Рис. 2.23.1
Определим число степеней свободы точки (рис.
2.23.2, а) и диска с различными кинематическими связями (рис. 2.23.2, б-д):
Рис. 2.23.2
Как видим, стержень или опорная связь уменьшают
число степеней свободы на единицу, шарниры – на два, припайки – на три.
2.5. Порядок и процедуры кинематического анализа
В ходе кинематического анализа расчётной схемы
сооружения даются ответы на два главных вопроса:
1) достаточно ли суммарное число внешних и
внутренних связей в системе для того, чтобы при правильном их размещении обеспечить её геометрическую неизменяемость?
2) правильно ли расставлены связи?
Следует обратить внимание на то, что первый
вопрос ещё не предполагает изучения правильности расстановки связей – он нацелен на оценку их количества.
В связи с этим в кинематическом анализе
выделяются два последовательных этапа:
1) количественный анализ;
2) качественный (структурный) анализ.
2.5.1. Количественный анализ
К о л и ч е с т в е н н ы й а н а л и з – это исследование расчётной схемы сооружения,
заключающееся в оценке баланса (соотношения) суммарного числа степеней свободы
дисков системы до наложения на них внешних и внутренних связей (т.е.
несвязанных дисков) и суммарного числа внешних и внутренних связей
системы, в
пересчёте на связи первого типа.
Указанный пересчёт объясняется тем, что именно
связь первого типа способна устранять, при правильном её использовании, одно
возможное взаимное перемещение (линейное или угловое) соединяемых дисков, т.е.
одну степень свободы.
2.5.1.1. Количественная оценка степеней свободы
и числа связей
Суммарное число степеней свободы несвязанных
дисков системы обозначим n∆, а суммарное число условных (в пересчёте)
связей первого типа – nc.
Для правильной оценки соотношения между n∆ и nc (больше, меньше, равны) необходимо, изучив
расчётную схему сооружения, заранее строго определить, какие элементы системы считать дисками,
а какие рассматривать как связи. При этом имеет смысл учитывать возможности,
проиллюстрированные выше на рис. 2.20. Один и тот же элемент не может одновременно быть и диском, и связью; связи должны налагаться только на диски,
но не друг на друга.
После номинации дисков выполняется формальное
выявление внешних и внутренних связей в системе по следующему алгоритму:
1) определяются возможные комбинации соединений дисков друг с другом, исключая диск
«земля» (например, четыре диска системы D1 , D2 , D3 , D4 могут иметь соединения в следующих шести
сочетаниях: D1↔D2 , D1↔D3 , D1↔D4 , D2↔D3 , D2↔D4 , D3↔D4 );
2) каждая комбинация проверяется на предмет реального существования предсказанных в главе 2.3
возможных соединений соответствующих дисков, и в случае наличия связей (одной
или нескольких) определяются их типы;
3) дополнительно для всех дисков
проверяется наличие связей между
точками одного и того же диска (примеры – на рис. 2.24: связь 3-го типа (припайка) в узле А диска D1 (криволинейного стержня с замкнутой осью), связь 2-го типа
(шарнир) в диске-стержне D2 и связь АВ 1-го типа (линейная) в
диске D3;
4) во всех точках, где имеются соединения с диском «земля» (опоры), т.е. внешние связи, оцениваются их типы и
подсчитывается число эквивалентных им связей 1-го типа.
Число дисков системы (без учёта диска «земля»)
обозначим D, число внутренних связей 1-го типа – С, 2-го типа (шарниров в плоских системах) – Н, 3-го типа (припаек) – П, суммарное число внешних связей (с диском «земля»), пересчитанных
на связи 1-го типа – С0.
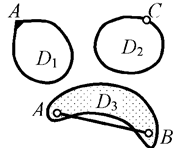
Рис. 2.24
Рассмотрим примеры реализации вышеприведённого
алгоритма, учитывая, что для одной и той же системы возможны различные варианты
представления о её дисках и связях.
Например, систему с расчётной схемой по рис.2.25, а, можно считать состоящей из шести дисков (D1 , D2 ,…, D6 на рис.2.25, б), тогда
внутренними связями являются три припайки П1 , П2 , П3 между дисками D1↔D2 , D2↔D5 , D3↔D4 и три шарнира Н1 , Н2 , Н3 между дисками D1↔D6 , D5↔D6 , D2↔D3 (или D5↔D3 – альтернативно, но не
одновременно с D2↔D3 !, так как диски D2 и D5 соединены жёстко, и в
соединении с диском D3 формально выступают как
единый диск, учитываемый только один раз). Соединения с «землей» имеются в
точках А, В и G, где расположены соответственно неподвижная защемляющая опора
(внешняя связь 3-го типа), подвижная шарнирная опора (внешняя связь 1-го типа)
и неподвижная шарнирная опора (внешняя связь 2-го типа). Суммарное число
эквивалентных связей первого типа равно 3 + 1 + 2 = 6.
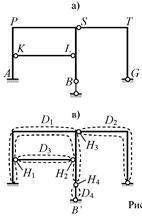
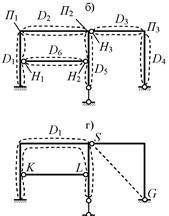
Рис. 2.25
Во втором варианте (см. рис.2.25, в) П-образная
левая часть системы состоящая из трех стержней, жёстко соединенных в
узлах Р и S, считается диском D1 (эту часть также
можно рассматривать просто как диск в виде стержня с ломаной осью). Аналогично
назначен диск D2 . Горизонтальный элемент KL рассматривается как диск D3 . Формально к дискам отнесен также опорный стержень в точке В, обозначенный как диск D4. Четыре диска соединяются друг с другом только шарнирами – их
четыре (Н3 и Н4 – соответственно между
дисками D1↔D2 , D1↔D4 и два – Н1 и Н2 между D1↔D3). Опоры в точках А и G – такие же, как в первом варианте, а посредине
диск D4 имеет опорный шарнир в точке В’. Суммарно опоры эквивалентны 3 + 2 + 2 = 7 связям
первого типа.
В третьем варианте (см. рис. 2.25, г)
рассматривается только один диск D1. Поэтому внутренних связей, соединяющих его с другими дисками,
нет. Стержень KL, схема которого точно соответствует определению линейной связи
согласно рис. 2.7, учитывается как внутренняя связь 1-го типа между точками K и L одного диска (в соответствии с п. 3 приведённого
выше алгоритма). Правый стержень с ломаной осью отнесён к внешним связям в
качестве условной линейной связи с осью SG (по аналогии с рис. 2.20, б). Внешние связи
(опоры) в точках А и В – такие же, как в первом варианте. Суммарное
число эквивалентных внешних связей 1-го типа: 3 + 2 + 1 = 5.
Таким образом, в трёх рассмотренных вариантах
номинации дисков и связей имеем:
– по рис. 2.25, б: D = 6, П = 3, H = 3, C = 0, C0 = 6;
– по рис. 2.25, в: D = 4, П = 0, H = 4, C = 0, C0 = 7;
– по рис. 2.25, г: D = 1, П = 0, H = 0, C = 1, C0 = 5.
Возможны и иные варианты представления о дисках
и связях той же системы.
В некоторых точках (узлах) могут соединяться
шарнирно или жёстко более двух дисков (рис. 2.26, а, б соответственно).
Шарнирный узел (см. рис. 2.26, а) по
существу представляет собой
попарное соединение дисков бесконечно близко расположенными шарнирами (см. рис.
2.26, в), условно изображаемыми с общим центром (осью вращения). Поэтому шарнир, соединяющий более двух дисков,
называется кратным (или сложным). Очевидно, что в немобъединены nD,уз – 1 обычных (иногда говорят – простых) цилиндрических шарниров;
здесь nD,уз – количество дисков, соединяемых в узле кратным шарниром. В
случае, показанном на рис. 2.26, а, соединение дисков в узле учитывается как
три простых шарнира (Нуз = nD,уз – 1 = 4 – 1 = 3). Заметим, что если какой-либо стержень из сходящихся в шарнирном узле отнесён не к дискам, а к связям
1-го типа, то при подсчете кратности шарнира он, конечно, не учитывается.
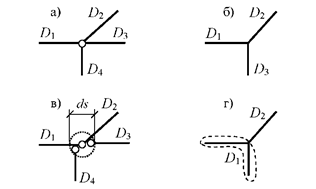
Рис. 2.26
Аналогично кратной, т.е. соединяющей более двух
дисков, может быть и припайка (см. рис. 2.26, б), эквивалентная
также nD, уз – 1 простым припайкам (двум в узле, изображённом на рис. 2.26, б: Пуз = nD,уз – 1 = 3 – 1 = 2).
Очевидно, что в случае, приведённом на рис.
2.26, г, несмотря на наличие трёх сходящихся в узле стержней, припайка не
является кратной, так как два из трёх стержней заранее объединены в диск D1. Если какой-либо из стержней, жёстко соединённых в узле, принят в
качестве связи 3-го типа (в соответствии с рис. 2.26, в), то он не
учитывается в nD,уз.
Расчётная схема сооружения может содержать узлы,
в которых осуществляется одновременное соединение дисков с помощью шарниров и
припаек (например, узел Sна рис. 2.25, б), в том числе и кратных. Такие узлы, в отличие от
тех, где соединение дисков только шарнирное (шарнирные узлы) или только
жёсткое (жёсткие узлы), называются узлами с комбинированным соединением дисков. Для правильной оценки числа эквивалентных простых шарниров и
припаек требуется аккуратная оценка кинематических свойств комбинированного
соединения. Например, в узле, изображённом на рис. 2.27, а, жёстко соединяются
три диска-стержня D1, D2 и D3 (соответственно
кратная припайка эквивалентна 2 простым), а кратный шарнир связывает четыре
диска – D4 , D5 , D6 и объединённый диск DI = D1 + D2 + D3 и поэтому эквивалентен трём простым; следовательно, Пуз = 2, Нуз = 3.
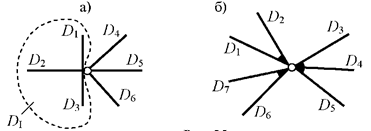
Рис.2.27
В комбинированном узле, показанном на рис.2.27,
б, соединяются семь дисков с помощью двух простых и одной кратной припайки,
эквивалентной двум простым, а также кратного шарнира, связывающего три укрупнённых диска D1 + D2 , D6 + D7 и D3 + D4 + D5 . В итоге для узла имеем Пуз = 4, Нуз = 2.
Замечание, не имеющее
прямого отношения к кинематическому анализу,но полезное в дальнейшем:
Особенности соединения нескольких элементов в
шарнирном узле реальной конструкции определяются конкретным инженерным
воплощением узла: возможно соосное объединение элементов на общем
цилиндрическом вкладыше – в этом случае кратный шарнир в расчётной схеме появляется
естественным образом; могут применяться также различные сочетания шарнирных
соединений с небольшими расстояниями между осями шарниров – при формировании
расчётной схемы конструкции эти малые несоосности могут игнорироваться,
что опять же приводит к возникновению кратного шарнира. Каким образом появился
кратный шарнир в расчётной схеме сооружения, для кинематического анализа не
имеет никакого значения. Однако на стадии расчёта конструкции целесообразно
конкретизировать соединение дисков в узле, обозначив определённую комбинацию
простых шарниров – это позволяет составить чёткое представление о реакциях
связей и о том, к каким именно соединяемым дискам те или иные из них должны
быть приложены.
Разные варианты внутренней структуры сложного
шарнирного узла отличаются лишь «игрой сил» в самом узле, т.е. различными
комбинациями реакций связей простых шарниров. Для реальной конструкции это,
несомненно, имеет значение в области узла, малой в сравнении с размерами
элементов конструкции, но за пределами этой области особенности внутреннего
распределения сил в ней практически не влияют на усилия в системе. Поэтому если
сведения о конкретном конструктивном решении узла отсутствуют, то можно задать
в нем любое соединение дисков простыми шарнирами, выбрав наиболее удобный из
нескольких вариантов. Например, альтернативой модели, приведённой на рис.2.26,
в, является прикрепление
диска D4 шарниром не к D1 , а к D2 или D3 (возможны и другие комбинации соединений).
После того, как
выполнено разделение элементов расчётной схемы сооружения на диски и связи (NB: не должно остаться
ни одного элемента, не отнесённого к одной или другой категории!), выполняется
вычисление и последующее сопоставление n∆ и nc . Суммарное число
степеней свободы несвязанных дисков определяется исходя из того, что каждый
жёсткий пространственный диск, как установлено выше, обладает шестью степенями
свободы, а плоский – тремя.
Тогда если, как принято ранее, число дисков системы – D, имеем
При выводе формулы для суммарного числа внешних
и внутренних связей nc (в пересчёте на связи 1-го типа) учитывается,
что пространственная припайка эквивалентна шести простым связям (плоская – трём), шарниры плоских
систем (цилиндрические и поступательные) учитываются как две связи 1-го типа,
шаровой шарнир в пространственной системе – как три:
При использовании формулы (2) для
пространственной системы все соединения, не подпадающие под признаки припайки,
шарового шарнира или связи 1-го типа, непосредственно представляются как
комбинации соответствующего числа простых связей.
2.5.1.2. Необходимое условие геометрической
неизменяемости
Очевидно, что для обеспечения геометрической
неизменяемости системы необходимо отсутствие возможных перемещений (степеней
свободы) у её дисков после наложения на них всех выявленных внешних и
внутренних связей. А это возможно лишь в том случае, когда суммарное число
связей nc не меньше суммарного числа степеней свободы n∆ несвязанных дисков, т. е.
nc≥ n∆, (3)
в противном случае останутся некоторые неустраненные степени свободы, что является признаком геометрически изменяемой системы. Если ввести для характеристики соотношения n∆ и nc их разность
W= n∆ - nc , (4)
то условие (3) примет вид
W≤0. (5)
Неравенства (3) и (5) выражают необходимое, но недостаточное условие
геометрической неизменяемости системы.
Недостаточность условия неизменяемости в виде
(3) или (5) проявляется в том, что оно имеет сугубо количественный характер и не может учесть возможных дефектов в
размещении связей. Не исключена ситуация, когда характеристика W неположительная, т.е. условие (5) выполняется,
но связи в системе распределены неправильно: например, с переизбытком в
некоторых частях, тогда в других частях их может быть недостаточно, и там остаются
некоторые степени свободы дисков. Следовательно,выполнение необходимого
условия геометрической неизменяемости не гарантирует того, что система в
действительности будет неизменяемой.
Результатом проверки выполнения условия (5) является одно из
двух альтернативных
заключений:
1) система может быть неизменяемой (если получено W = 0 или W < 0);
2) система геометрически изменяема (при W > 0) и является механизмом.
Вычисление характеристики W и проверка выполнения необходимого условия
геометрической неизменяемости составляют содержание 1-го этапа кинематического
анализа – количественного анализа расчётной схемы сооружения. В представленном на
рис. 2.1 алгоритме кинематического анализа количественный анализ является
частью процедуры проверки, обозначенной оператором 1, и обеспечивает
немедленный выход из него при W > 0 (ответ «нет»). В случаях W = 0 или W < 0 для выхода с ответом «да» или «нет» необходимо
дальнейшее исследование расчётной схемы сооружения – структурный анализ
системы.
Для вычисления характеристики W служат формулы, получаемые подстановкой в (4)
выражений (1) и (2):
Рассмотрим определение W для трёх вариантов описания плоской стержневой
системы (см. рис. 2.25, б, в, г):
– по варианту 1: W = 3∙6-(3∙3+2∙3+0+6)=-3;
– по варианту 2: W = 3∙4-(3∙0+2∙4+0+7)=-3;
– по варианту 3: W = 3∙1-(3∙0+2∙0+1+5)=-3.
Во всех трёх вариантах получено, как и следовало
ожидать, одно и то же значение W = –3 < 0. Заключение по
результатам количественного анализа: система может быть геометрически неизменяемой, так как связей количественно хватает (и даже
имеется некоторый их избыток), чтобы при правильном их размещении обеспечить
устранение всех степеней свободы дисков системы.
Для системы, изображённой на рис. 2.28, после обозначения дисков D1 , D2 ,…, D5 имеем: D = 5; П = 0; Н = 4 (в узлах К, L и кратный в узле G); С = 0; С0 = 7 (опорные шарниры А и С, каждый из которых эквивалентен двум
связям 1-го типа, и неподвижная защемляющая опора В – три связи);
W = 3∙5-(3∙0+2∙4+0+7) = 0 – система может быть геометрически неизменяемой.
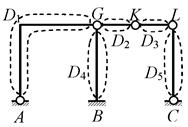
Рис.2.28
В системе, схема которой показана на рис. 2.29,
выделены шесть дисков ( D = 6 ). Жёстких узлов нет ( П = 0 ). Шарниров четыре (все простые –
соединяют диски попарно: D1↔D2 , D2↔D3 , D3↔D4 , D4↔D5 ), т.е. Н = 4. Внутренние связи 1-го типа – стержни CS, SJ, TP и TL; С = 4. Внешних связей –
пять (С0 = 5): стержни АС и LK, а также три связи в опорах В и G. Находим W = 3∙6-(3∙0+2∙4+4+5)=1> 0 – система геометрически изменяемая.
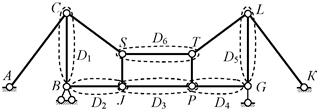
Рис. 2.29
Можно стержень JР отнести не к дискам, а к внутренним линейным связям, тогда D = 5, П = 0, H = 2, C = 5, Со = 5 и W = 3∙5-(3∙0+2∙2+5+5)=1> 0 – результат не изменился.
Заметим, что в обоих вариантах диск D6 необходим, так как иначе стержень SТ должен рассматриваться как связь 1-го типа, и в узлах S и Т связи будут соединяться только друг с другом,
что недопустимо.
Замечание: иногда характеристику W называют числом степеней свободы системы.
Использование такого не вполне корректного термина может стать причиной неверного вывода: ведь если вложить в W смысл, отвечающий названию, то результат W = 0 формально следует истолковывать как отсутствие у системы степеней свободы и, следовательно, оценивать систему как
геометрически неизменяемую; но это не всегда соответствует истине. Например, в случае, представленном на рис. 2.28, W = 0, но в действительности существует очевидная возможность конечных перемещений дисков в правой части системы (рис.
2.30), полностью определяемых углом α; следовательно, у системы всё-таки имеется одна
степень свободы. Объяснение этой ошибки заключается в том, что названием
«число степеней свободы системы» характеристике W придается
несвойственное ей содержание качественного характера,
выводящее на заключение о кинематическом качестве системы, в то время как W служит лишь для
оценкиколичественной достаточности или недостаточности связей для
возникновения возможности устранения всех степеней свободы
несвязанных дисков (вопрос о том, реализуется или нет указанная возможность, на
этапе количественного анализа
системы вообще не рассматривается). Некорректность термина «число степеней
свободы системы» в применении к характеристике W особенно отчётливо проявляется в случае
отрицательного её значения.
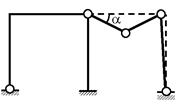
Рис. 2.30
Как уже отмечалось выше, если в результате
выполнения 1-го этапа (количественного анализа) обнаружено, что расчётная схема
системы удовлетворяет необходимому условию геометрической неизменяемости ( 5 ), то осуществляется её
качественный (структурный) анализ, представляющий собой 2-й этап
кинематического анализа.
2.5.2. Структурный анализ
К а ч е с т в е н н ы й ( с т р у к т у р н ы й
) а н а л и з – это исследование структуры расчётной
схемы сооружения, заключающееся в проверке правильности расположения связей,
выявлении возможных дефектов соединения дисков и завершающееся определением
кинематического качества (природы) системы (её геометрической неизменяемости,
изменяемости или мгновенной изменяемости).
В ходе структурного анализа дается оценка
кинематического качества каждой внешней и внутренней связи на основании
упоминавшегося выше кинематического признака классификации связей. По этому признаку классифицируются
только простые (линейные и
угловые) связи, которые
подразделяются на необходимые, лишние и ложные. Имеющиеся в системе сложные связи
(шарниры, припайки) предварительно представляются как соответствующие
комбинации простых связей.
2.5.2.1. Классификация связей по кинематическому
признаку
Н е о б х о д и м ы е с в я з и – это связи, удаление которых вызывает изменение кинематической
природы системы (геометрически неизменяемая система превращается в
геометрически изменяемую или мгновенно изменяемую, мгновенно изменяемая система
становится геометрически изменяемой).
Л и ш н и м и называются связи, при удалении которых
кинематическая природа системы не изменяется, но эти связи ограничивают перемещения в деформируемой системе.
Л о ж н ы е с
в я з и – такие, которые не оказывают никакого влияния ни на
кинематическую природу системы, ни на перемещения в ней, определяемые с учётом
деформации элементов.
Иными словами, при удалении ложной связи в системе ничего не изменяется – ни в случае учёта
деформаций её элементов, ни в предположении об условной идеальной жёсткости
материала.
Как видно из вышеприведённых определений, связи трёх разных видов различаются по последствиям удаления связи из
системы. Поэтому кинематический признак
связи формулируется с
использованием характерного геометрического параметра – возможного перемещения δS в системе с удалённой данной связью по её
направлению, в предположении о недеформируемости дисков и связей (по гипотезе отвердения). Если
исследуемая связь линейная, то δS – это проекция взаимного линейного перемещения
точек А и В соединяемых связью
дисков (см. рис.2.7) на направление оси связи. В случае угловой связи
перемещение δS – угол взаимного поворота узлов (сечений) в точках А иВ (см. рис. 2.8).
Очевидно, что в случае необходимой связи
результатом её удаления должно быть возникновение степени свободы – перемещения
по её направлению, следовательно,δS ≠0 – это и есть кинематический признак
необходимой связи. При удалении лишней или ложной связи новая степень свободы
не возникает, поэтому δS =0 – это кинематический признак, общий для
лишней и ложной связи. Чтобы различать их, используется дополнительный
критерий, в котором оценивается также возможное перемещение, но в деформируемой системе с удалённой исследуемой связью, по её направлению – 
. Как следует из определения лишней связи, для
неё ≠0, а в случае ложной связи = 0.
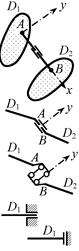
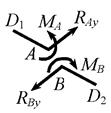
Дадим оценку кинематической природы внешних
линейных связей 1, 2 и 3 (рис.2.31, а). Удалив связь 1, обнаружим, что
возникает возможность перемещений в левой части системы, даже если считать
диски и связи абсолютно жёсткими (см. рис. 2.31, б), при этом проекция
линейного перемещения точки А (точка В неподвижна) на направление связи 1 получается
отличной от нуля (δ1≠0), следовательно, связь 1 – необходимая. После удаления связи 2 (при этом связь 1, уже
исследованная ранее, остаётся на своем месте) получаем систему, изображённую на
рис. 2.31, в. Полагая её стержни и связи недеформируемыми,
обнаружим, что никаких перемещений в ней, в том числе и по направлению
удалённой связи 2, возникнуть не может, т.е. δ2 = 0 – по этому признаку связь 2 либо лишняя, либо ложная.
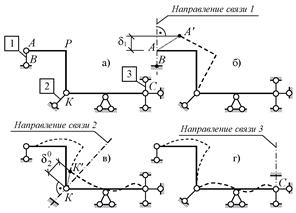
Рис.2.31
Для уточнения отказываемся от гипотезы
отвердения и рассматриваем некоторое возможное (не противоречащее
связям) произвольное деформированное состояние системы – на рис. 2.31, в оно изображено штриховой линией. По направлению связи 2 в узле К имеется перемещение 
≠0 – значит, связь 2 – лишняя. Наконец, удалив связь 3, получаем систему, показанную на рис.
2.31, г, – в ней точка С не может перемещаться ни в случае отсутствия деформаций элементов,
ни в деформированном состоянии, т.е. δ3= 0 и 
=0 – признак того, что связь 3 – ложная.
Лишние и ложные связи с количественной точки
зрения являются избыточными, так как они не нужны для обеспечения
геометрической неизменяемости системы – для этого достаточно только необходимых
связей. Число избыточных связей определяется как nизб.св. = nc – n∆ = – W.
Несмотря на своё название, лишние связи, тем не менее, нужны для реализации определённых
эксплуатационных качеств сооружения и появляются в расчётной схеме как
результат принятия тех или иных инженерных решений при проектировании
конструкций. Более того, в действительности систем без лишних связей не бывает
– они возникают лишь в результате формирования расчётных моделей сооружений с
идеализацией их реальных свойств (в частности, если пренебрегать трением в
шарнирах, опорах и т.п.).
А вот ложные связи не нужны вообще,
их можно рассматривать как «паразитные»; они должны быть выявлены и удалены из системы до начала её расчёта – в противном случае математическое решение
задачи определения усилий и перемещений в сооружении окажется невозможным. В
большинстве случаев специального исследования по критерию = 0 для обнаружения ложной связи не требуется,
так как наглядным признаком её обычно является то, что она наложена на уже неподвижную точку (например, в системе на рис. 2.31 – связь 3 в
точке С, которая и без этой связи уже неподвижна,
будучи закреплена горизонтальной и нижней вертикальной жёсткими связями 1-го
типа).
Поскольку «сортировка»
избыточных связей – разделение их на лишние и ложные – производится путем учёта
деформаций элементов системы (заметим, что это единственная процедура
кинематического анализа, в которой не применяется гипотеза отвердения), то при
разных исходных предпосылках о характере деформирования рассматриваемой системы
возможны и разные оценки кинематического качества одной и той же избыточной
связи – в одних случаях она может быть определена как лишняя, а в других – как ложная. Например, если систему,
показанную на рис. 2.32,
предполагается в дальнейшем рассчитывать с учётом всех видов деформаций стержневых элементов (изгиб, сдвиг,
растяжение-сжатие), то горизонтальная связь в точке С – лишняя, так как её удаление не изменяет
кинематическую природу системы, которая остаётся геометрически неизменяемой; но точка С получает возможность перемещаться горизонтально из-за продольных деформаций стержней АВ и ВС – следовательно, ≠0. Но если, как это часто
делается в расчётах рамных
систем, продольные деформации (укорочения-удлинения) стержней считать
пренебрежимо малыми в сравнении с перемещениями, возникающими при искривлениях
элементов от их изгиба, а сами «изгибные» перемещения – малыми, то при
деформации горизонтального стержня АВСрасстояние между точками А и С изменяться не будет,
т.е. точка С останется неподвижной даже при удалённой горизонтальной связи – таким образом, = 0, и указанная связь оказывается ложной.
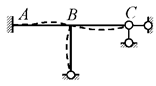
Рис.2.32
Если в реальном сооружении со схемой по рис. 2.33 допускается
возникновение больших (соизмеримых с длинами элементов) перемещений,
обусловленных изгибом, то и величину следует оценивать при больших перемещениях
(рис.2.33) – видно, что в этом случае ≠0, и горизонтальная связь в точке С – лишняя.
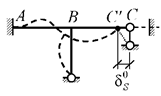
Рис.2.33
Приведённые примеры подтверждают обязательность
корректного и строгого учёта исходных предпосылок и рабочих гипотез,
определяющих особенности деформирования рассматриваемой системы, при выполнении
её структурного анализа.
Выше уже указывалось, что по количественной
оценке лишние и ложные связи входят в одну группу, являясь избыточными связями. Можно также заметить, что у необходимых
и лишних связей есть общее свойство, заключающееся в том, что и те, и другие накладывают
ограничения на перемещения системы (правда, в случае лишней связи – на
перемещение, определяемое с учётом деформаций элементов). Следовательно, и
необходимые, и лишние связи влияют на кинематические свойства системы и поэтому
объединяются в категорию кинематических связей, в отличие от ложных связей, являющихся некинематическими.
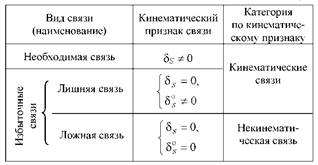
В табл. 2 дано обобщение приведённых выше
сведений о классификации связей по кинематическому признаку, а также
сопутствующих терминов.
Таблица 2
2.5.2.2. Некоторые особенности анализа
кинематической природы связей
В рассмотренном примере (см. рис. 2.31) связь 1
однозначно (безусловно) определена как необходимая. Относительно лишних и
ложных связей такой однозначности нет. В частности, в узле С ложной связью может быть объявлена либо связь 3
(как это сделано в примере), либо нижняя вертикальная связь, если предположить,
что она введена в узел С после его закрепления верхней вертикальной и
горизонтальной линейными связями. Таким образом, существует альтернатива
выявления ложной связи в узле С – для её разрешения должен быть обозначен определённый порядок
наложения связей на узел, после чего делается заключение о том, какая именно из
двух вертикальных связей рассматривается как ложная. Не столь очевидно решение
вопроса о лишних связях. Если в той же системе (см. рис. 2.31) последовательно оценивать каждую из внешних связей (кроме
необходимой), оставшихся после исключения ложной, то формально все они окажутся
лишними, причём их число превысит найденное количественным анализом число
избыточных связей nизб.св. = – W (здесь W – за вычетом удалённых ложных связей). Возникновение этого
противоречия свидетельствует о некорректности процедурыпоодиночного последовательного перебора всех связей, не
являющихся необходимыми, на предмет определения лишних. Правильный подход
состоит в том, что выявлять лишние связи нужно все одновременно, т.е. группой, исходя из того, что для системы с уже исключёнными ложными связями число лишних связей nлишн.св. = nизб.св. = – W. Рассматриваются разные возможные варианты
групп, состоящих каждая из nлишн.св. предположительно лишних связей; причем к этому
моменту необходимые связи должны быть обнаружены, чтобы не быть случайно
включёнными в анализируемую группу.
Алгоритм действий таков:
1) одновременно удаляются все связи,
включённые в исследуемую группу;
2) в системе с удалённой группой предположительно лишних связей оцениваются возможные перемещения δS и 
по направлению каждой из связей группы;
3) при невыполнении критерия δS=0 хотя бы для одной связи рассмотренная группа отвергается
как недопустимая; далее формируется новая группа, для которой выполняются
процедуры 1 – 3;
4) в качестве контроля проверяются связи,
оставшиеся в системе после удаления группы связей, признанных лишними по
результатам процедур 1 – 3, – все оставшиеся связи должны оказаться
необходимыми.
Например, после удаления
в системе, представленной на рис. 2.31, а, ложной связи 3 (других
ложных связей нет, если не пренебрегать продольными деформациями стержней; в
противном случае ложной будет и горизонтальная связь в узле С)
система принимает вид по схеме рис. 2.31, г. Выполняя её количественный анализ,
имеем: D = 2, П= 0, H =1, С = 0, Со = 6, тогда W =3D-(3П+2Н+С+С0)=3∙2-(3∙0+2∙1+0+6)=-2; nлишн.св.= –W = 2.
Рассматривая группу из двух связей, образующих
среднюю шарнирную неподвижную опору, после их удаления получаем систему, изображённую на рис. 2.34. Очевидно, что без
учёта деформаций стержней получается δ1 = 0 и δ1 = 0, а в деформируемой системе 
и 
– значит, указанные две связи – лишние. Легко убедиться в том, что все остальные связи в системе (см. рис. 2.34) – необходимые.
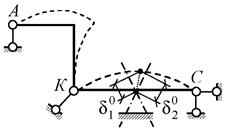
Рис.2.34
Возможны и другие варианты групп лишних связей,
например, две опорные связи в точке С или связь в точке К и горизонтальная связь в точке С. Общее количество
исследуемых вариантов групп предположительно лишних внешних связей в рассматриваемой системе определяется как число сочетаний
из пяти внешних связей (необходимая связь в точке А не учитывается) по две:
Среди них есть одна недопустимая – группа из связи в точке К и вертикальной связи в точке С (после их удаления получается δ1≠0 и δ2≠0 – рис.
2.35).
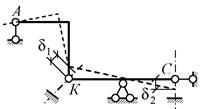
Рис.2.35
Если учитывать возможность отнесения к лишним связям наряду с внешними
также и внутренних связей (например, трёх в припайке Р на рис. 2.31, а), то число вариантов групп
становится значительно больше, возрастая до 28. Однако практической
необходимости рассматривать все возможные варианты нет – достаточно
проанализировать несколько наиболее характерных из них.
Более того, для большинства расчётных схем
сооружений вообще можно не выполнять подробного исследования кинематической
природы всех связей. Вместо этого структурный анализ сводится к воспроизведению
последовательности операций по образованию (синтезу) системы из исходного
набора несвязанных дисков наложением связей, предусмотренных расчетной схемой.
При этом каждая операция заключается в соединении нескольких дисков (исходных
или созданных путем укрупнения) с помощью определённой комбинации связей.
Результатом очередного шага (операции) синтеза должно быть либо получение
геометрически неизменяемой части системы (если это возможно обеспечить набором
связей, имеющихся в расчётной схеме), либо выявление дефектов в расположении
связей. В большинстве случаев разные ситуации в процессе синтеза системы могут
быть сведены к применению типовых способов
геометрически неизменяемого соединения элементов (дисков), изложенных в табл. 3 применительно к плоским
системам.
2.5.2.3. Типовые способы геометрически
неизменяемого соединения дисков
Типовые способы различаются набором соединяемых
объектов (в порядке усложнения: «диск и точка», «два диска», «три диска»,
причём точка формально может рассматриваться как диск бесконечно малых
размеров); связи – только необходимые.
Таблица 3
|
№ и название способа |
Содержание
способа (приёма) |
Схема соединения |
Требования к
расположению связей |
|
1. Соединение точки и диска |
Прикрепление точки к диску с помощью двух линейных
связей |
|
Оси связей не должны располагаться
на одной прямой |
|
2. Соединение двух дисков |
Соединение двух дисков с помощью трёх линейных связей |
|
Оси трёх связей не должны
сходиться в одной точке или быть параллельными |
|
Соединение двух дисков с помощью шарнира и линейной связи |
|
Ось линейной связи не должна
проходить через центр цилиндрического шарнира или быть
нормальной к оси поступательного шарнира |
|
|
3. Соединение трёх дисков |
Попарное соединение трех дисков с помощью трёх пар линейных связей |
|
Три точки (А, В, С)
пересечения направлений осей пар связей не должны лежать
на одной прямой |
|
Соединение трёх дисков с помощью трёх цилиндрических
шарниров |
|
Шарниры А, В и С не должны лежать на одной прямой |
Легко заметить, что типовые способы и приёмы
различаются только формально наборами дисков и связей, но по существу могут в
ряде случаев являться вариантами описания одного и того же соединения. Так,
способ 1 и приём 2б эквивалентны приёму 3б, если стержни рассматривать не как
связи 1-го типа, а как диски. Используя понятие фиктивных (условных) шарниров,
можно обнаружить сходство приёмов 3а и 3б. Приём 2а трансформируется в 2б
введением фиктивного шарнира как точки пересечения направлений осей каких-либо
двух из трёх линейных связей. Из этого замечания следует, что в процессе
синтеза системы некоторая операция соединения дисков может истолковываться
по-разному – с применением того или иного типового способа (приёма), наиболее
очевидного и удобного в каждом конкретном случае. Более того, отметимнеобязательность сохранения на этапе структурного анализа той же
номинации дисков и связей, которая была введена и использована ранее в
количественном анализе. При выполнении исследования структуры системы может
оказаться удобным иное представление о дисках и связях – этим имеет смысл
рационально пользоваться в целях упрощения.
2.5.2.4. Алгоритм структурного анализа
1) в первую очередь обнаруживается диск с
достаточным (не менее трёх) числом связей с «землей» и проверяется правильность
наложения на него внешних связей сопоставлением с типовым способом 2 (при этом
могут быть выявлены избыточные связи); в случае отсутствия такого диска
целесообразно осуществить, если это возможно, предварительное укрупнение
структуры системы путём соединения исходных дисков типовыми способами, в
результате чего среди полученных крупных дисков могут появиться такие, у
которых внешних связей достаточно для образования геометрически неизменяемой
части системы;
2) если даже после укрупнения не удаётся
обнаружить ни одного диска, геометрически неизменяемо соединённого с «землей»,
то выявляются два диска с не менее чем двумя внешними связями каждый,
которые рассматриваются вместе с диском «земля» на предмет соединения по способу 3; если
же и этот вариант первой операции синтеза не удаётся применить, то это
означает, что система не может быть образована с помощью типовых способов и
должны использоваться другие подходы (изложение их будет дано позднее);
3) далее производится присоединение других
дисков, причем сначала рассматриваются возможности применения способов с более
простыми наборами соединяемых объектов («диск-точка», «два диска») и лишь в
последнюю очередь – приёмов соединения трёх дисков.
При выполнении каждой операции синтеза
обязательно проверяется выполнение требований к расположению связей (табл. 3) –
это позволяет обнаружить дефекты структуры расчётной схемы сооружения.
Если качественный анализ
приводит к заключению об отсутствии структурных дефектов (наличие лишних связей
к таковым не относится!), то делается вывод огеометрической неизменяемости
системы; при этом в случае отсутствия лишних связей ГНС является статически
определимой (количественный признак этого после выполнения
структурного анализа – W = 0); а
при W < 0 (есть лишние связи) – статически
неопределимой.
При обнаружении дефектов структуры система
квалифицируется как геометрически изменяемая или мгновенно изменяемая – в зависимости от того, какие перемещения – конечные или
бесконечно малые могут возникать в ней из-за ошибок в расположении связей.
Таким образом, в результате выполнения
структурного анализа даются ответы на все вопросы, обозначенные условными
операторами 1, 2 и 3 в блок-схеме алгоритма кинематического анализа,
приведённой на рис.2.1.
2.5.2.5. Системы с простой структурой
Системы, для которых качественный (структурный)
анализ расчётной схемы может быть полностью выполнен с использованием только
типовых способов (приёмов) геометрически неизменяемого соединения дисков,
называются с
и с т е м а м и с п р о с т о й с т р у к т у р о й.
Рассмотрим примеры структурного анализа плоских
стержневых систем. Образование (синтез) рамы (см. рис. 2.25, а), для которой в
результате количественного анализа получено W = –3 (три избыточные связи), может быть
представлено следующим образом:
1) диск D1 в виде ломаного
стержня АРSB жёстко прикрепляется к
диску «земля», что эквивалентно соединению двух дисков с помощью трёх
связей (типовой приём 2а в табл. 3); результат этой
операции – геометрически неизменяемая система (диск DI = «земля» + D1) только с необходимыми
связями, представленная на рис. 2.36, а, где
штрихпунктирными линиями обозначены оси стержней в
проекте сооружения;
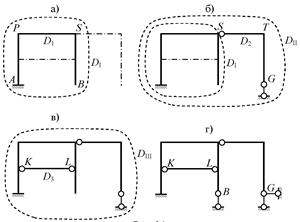
Рис.2.36
2) к геометрически неизменяемой системе – диску DI присоединяется диск D2 (ломаный стержень STD) – рис. 2.36, б – с помощью цилиндрического шарнира в точке Ти одной (вертикальной) из двух линейных связей,
эквивалентных имеющейся в проекте сооружения шарнирной неподвижной опоре G; вторая линейная связь опоры пока что не
используется; соединение соответствует типовому приёму 2б, причём требование к
связям выполняется: направление оси линейной связи не проходит через шарнир Т; результат операции – диск DII = DI + D2 , образованный с помощью только необходимых связей и включающий в
себя диск «земля», следовательно, полученная на этом шаге синтеза система –
геометрически неизменяемая и не имеющая избыточных связей;
3) к геометрически
неизменяемой системе – диску DII присоединяется
диск D3 (стержень KL) – рис. 2.36, в – с
помощью двух цилиндрических шарниров в точках K и L, суммарно эквивалентных четырём линейным
связям, из которых одна – избыточная, так как типовые приёмы
соединения двух дисков по способу 2 (см. табл. 3) требуют лишь трёх связей; в качестве избыточной может рассматриваться,
например, горизонтальная линейная связь в эквивалентном представлении шарнира L, тогда шарнир K и вертикальная связь в точке L обеспечивают правильное прикрепление диска D3 к диску DII типовым приёмом 2б; результат – геометрически
неизменяемая система (диск DIII) с одной избыточной связью; к этому же
заключению можно прийти другим путём – рассматривая стержень KL в качестве линейной связи, соединяющей точки
одного и того же диска, – в этом случае она является избыточной;
4) в геометрически неизменяемую систему (диск DIII) с одной избыточной связью вводятся оставшиеся
неиспользованными предусмотренные исходной расчётной схемой сооружения две
линейные связи – вертикальная и горизонтальная в опорах В и G соответственно (см. рис. 2.36, г); получается система, схема
которой совпадает с заданной, с тремя избыточными связями;
5) проверяя избыточные связи (1 – вертикальную в
точке В, 2 – горизонтальную в точке G и 3 – стержень KL) по критериям δS = ? и = ? с определением возможных перемещений в
системе с одновременно удалёнными всеми избыточными связями в количестве nизб.св. = –W = 3 (см. рис. 2.36, б), находим, что с использованием гипотезы
отвердения δ1 = 0, δ2 = 0 и δ3 = 0, а с учётом деформаций 
и 
, следовательно, все избыточные связи – лишние;
6) вывод: заданная система геометрически неизменяемая, с простой структурой, с тремя лишними связями,
т.е. статически неопределимая.
Приведённое выше пошаговое изображение расчётной
схемы системы в процессе её синтеза (см. рис. 2.36) не является обязательным –
оно может быть полезным на начальной стадии выработки навыков выполнения
кинематического анализа (в дальнейшем заменяясь соответствующими мысленными
представлениями), а также в затруднительных случаях исследования структуры
многоэлементных систем.
Вместо подробного описания процедуры
качественного анализа можно применять сокращённую запись; в частности, для
рассмотренного примера:
1) «земля» + D1 = DI – по способу 2 (приём 2а – соединение двух дисков с помощью трёх
связей 1-го типа в форме неподвижной защемляющей опоры) ⇒ ГНС только с необходимыми связями;
2) DI + D2 = DII – по способу 2 (приём 2б – соединение двух
дисков с помощью шарнира S и линейной связи в точке G; ось связи не проходит через центр шарнира) ⇒ГНС только с необходимыми связями;
3) DII + D3 = DIII – соединение двух дисков с помощью двух
цилиндрических шарниров (четырёх эквивалентных простых связей; одна связь –
избыточная) ⇒ ГНС с одной избыточной
связью;
4) DIII + две линейные связи в точках В и G = геометрически неизменяемая система с тремя избыточными
связями;
5) для группы из трёх избыточных связей (п. 3 и
4): δ1 = 0, δ2 = 0, δ3 = 0, , . ⇒ все три связи – лишние;
6) вывод: заданная система геометрически неизменяемая, с простой структурой, с тремя лишними связями,
т.е. статически неопределимая.
Для системы, представленной на рис. 2.37,
количественный анализ дает
W =3D-(3П+2Н+С+С0)=3∙3-(3∙0+2∙2+2+3)=0
(D = 3 – стержни АРС, СSВ и СК; П = 0; Н = 2 – кратный шарнир С; С = 2 – стержни АК и КВ; С0 = 3).
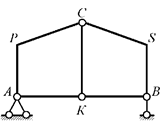
Рис.2.37
Следовательно, система может быть геометрически неизменяемой, и структурный анализ необходим.
В системе имеются три внешние связи (две шарнирные опоры), но ни у одного из
исходных дисков нет трёх связей с «землей». Поэтому для того, чтобы система была геометрически неизменяемой, нужно, чтобы
соединённые друг с другом её элементы образовывали бы единый диск. Для проверки
этой возможности выполняем предварительное укрупнение структуры. Используя
иное, чем в количественном анализе, представление о дисках и связях, синтез
системы осуществляем следующим образом:
1) (D1≡АРС) + точка К = DI – по способу 1 (прикрепление точки к диску с помощью двух линейных
связей – стержней АК и СК, направления осей
которых не совпадают);
2) DI + (D2≡СSB) + (D3≡КB) = DII – по способу 3 (приём 3б – соединение трёх
дисков с помощью трёх цилиндрических шарниров С, В и К, не лежащих на одной прямой);
3) DII + «земля» = ГНС – по способу 2 (приём 2а –
соединение двух дисков с помощью трёх линейных связей, оси которых не сходятся
в одной точке и не параллельны);
4) вывод: рассмотренная система геометрически неизменяемая, с простой структурой, статически определимая (W = 0).
Возможны варианты: например, соединение стержней АРС, СК и АК в диск D1 можно рассматривать по способу 3 (три диска и три шарнира А, С, К), а образование диска DII – по способу 2 (D1 и CSB с помощью шарнира С и связи КВ – приём 2б); перед
соединением диска DII с «землей» можно предварительно прикрепить к
«земле» точкуА по способу 1, а затем к
двум дискам (DII и «земля» + (∙)А) применить
приём 2б (соединение цилиндрическим шарниром А и линейной связью в точке В.
Количественный анализ системы со схемой по рис.
2.38, а показывает, что система может быть геометрически неизменяемой (если к
дискам отнести стержни КС и СР, а остальные стержни
считать связями 1-го типа, то D = 2, П = 0, Н = 1, С = 0, С0 = 4, тогда W =3∙2-(3∙0+2∙1+0+4)=0 – необходимое условие геометрической
неизменяемости выполняется).
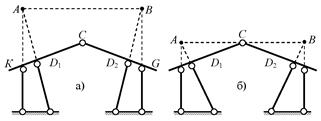
Рис.2.38
Структурный анализ начинается с поиска диска,
имеющего три связи с «землей». Таких дисков в системе нет. Поэтому первым шагом
синтеза не может быть соединение двух дисков, одним из которых является
«земля». Предварительное укрупнение структуры системы невозможно – нет ни одной
пары дисков, которые могли бы быть объединены типовыми способами.
Следовательно, нужно оценить возможность соединения трёх дисков – таковыми
оказываются «земля» и стержни КС и СG, связанные по способу 3 – тремя шарнирами, из
которых один реальный (С), а два других – фиктивные (А и В). Шарниры А, В и С не лежат на одной прямой, следовательно, система имеет правильную
структуру и является геометрически
неизменяемой, а ввиду отсутствия
избыточных связей (W = 0) – статически определимой.
На примере рассмотренной системы можно убедиться
в необходимости внимательной проверки выполнения требований к расположению
связей. Так, если изменить углы наклона внутренних стержней, то положение
фиктивных шарниров (точек А и В) изменится, и они могут оказаться на одной
прямой с шарниром С (см. рис. 2.38, б), а это – характерный признак
мгновенно изменяемого соединения дисков, вследствие чего и система в целом
должна быть квалифицирована как мгновенно изменяемая.
В расчётной схеме сооружения, показанного на
рис. 2.39, дисками могут считаться
стержни АС, СВ, GК, KL, LP и РS (D = 6), тогда H = 4 (простые шарниры в точках С,К, L и Р), С = 3 (внутренние
линейные связи ЕК, CL и ТР), П = 0, С0 = 7 (две опорные связи в точке А, одна в точке В и по две в точках G и S). Характеристика W =3∙6-(3∙0+2∙4+3+7)=0 – необходимое условие геометрической неизменяемости системы
выполняется.
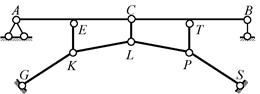
Рис.2.39
Но попытки осуществить синтез системы с помощью
типовых способов оказываются безуспешными – это невозможно, так как все диски
должны соединяться друг с другом и с диском «земля» одновременно, чтобы в
результате обеспечить геометрическую неизменяемость (а система в
действительности обладает этим качеством, но доказать это простейшими способами
нельзя).
2.5.2.6. Системы со сложной структурой
Системы, для которых качественный (структурный)
анализ расчётной схемы не может быть полностью выполнен с использованием только
типовых способов (приёмов) геометрически неизменяемого соединения дисков,
называются с
и с т е м а м и с о с л о ж н о й с т р у к т у р о й.
К таким системам относится сооружение,
изображённое на рис. 2.39.
Для выполнения качественного анализа систем со
сложной структурой могут применяться:
1) непосредственное исследование кинематической
природы связей (описание дано выше);
2) способ замены связей;
3) аналитический признак геометрической
неизменяемости системы.
При реализации первого подхода, как правило, не
требуется анализировать все связи системы – достаточно оценить некоторые из них
(а при W = 0 – возможно, даже одну). Например, в системе, представленной на
рис. 2.39, в силу того, что W = 0, все связи должны быть необходимыми – лишь в этом случае
структура её будет правильной. Проверим кинематическое качество какой-либо
связи, в частности, вертикальной линейной связи ЕК. Если это необходимая связь, то для неё должно быть выполнено
условиеδS≠0 (см. табл. 2).
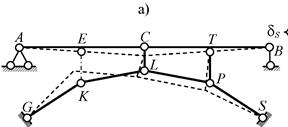
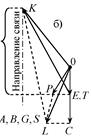
Рис.2.40
В соответствии с общей схемой выявления
кинематической природы связи удаляем её и полученной системе, превратившейся в
механизм с одной степенью свободы, задаём возможные перемещения, показанные
схематически штриховыми линиями на рис. 2.40, а (при этом используется гипотеза
отвердения). Искомая величина δS есть проекция на направление удалённой линейной
связи ЕК взаимного (относительного) перемещения соединяемых ею точек Е и К. Задав отличное от нуля
(числовое значение не играет никакой роли) малое перемещение какой-либо точки
(например, С), определяем перемещения всех остальных
характерных точек механизма (узлов, где соединяются диски). Для этого можно использовать:
а) мгновенные взаимные центры вращения дисков;
б) план мгновенных перемещений точек механизма
(подобен плану мгновенных скоростей).
На рис. 2.40, б представлен план перемещений, на
котором векторы 
и линии LС, PL, KL и РТ ортогональны одноимённым линиям на схеме
механизма (рис. 2.40, а). Отрезок ЕК на плане – полное
взаимное перемещение точек Е и К; его проекция на направление удалённой связи (в
рассматриваемом случае – на вертикаль) и есть перемещение δS. Оно получилось отличным от нуля – признак
того, что исследованная связь – необходимая. Её возвращение в систему устраняет
возможность возникновения любых перемещений при отсутствии деформаций элементов
(план перемещений вырождается в точку), следовательно, система – геометрически неизменяемая, а поскольку W = 0, то и статически определимая.
В двух других вышеуказанных вариантах
качественного анализа систем со сложной структурой, основанных на способе
замены связей и аналитическом признаке геометрической неизменяемости, используются, в отличие от остальных подходов, статические характеристики связей.
Сущность способа замены связей состоит в следующем. Если структура системы правильная, то любое
конечное воздействие вызывает в ней, в случае устойчивого равновесия,
единственное напряжённо-деформированное состояние с конечными значениями
перемещений и силовых факторов, в том числе реакцию S некоторой связи, кинематическую природу которой
требуется определить. Для системы со сложной структурой может оказаться
трудоёмкой процедура составления и решения уравнений, с помощью которых
находится S. Для упрощения осуществляется замена связей:
исследуемая связь удаляется с приложением вместо неё реакции S, и в систему вводится новая (заменяющая) связь,
причём таким образом, чтобы получилась система с простой структурой. Реакция заменяющей связи 
, согласно принципу суперпозиции, может быть
представлена как сумма её составляющих – 
(от некоторого воздействия –
нагрузки) и 
(от реакции S удалённой исследуемой связи):
Величина может быть записана в виде 
, где 
– реакция заменяющей связи от усилия S = 1. Поскольку силовой фактор S обеспечивает равновесие системы с удалённой
связью при действии нагрузки, то заменяющая связь в работу не включается, и
усилие в ней равно нулю: 
, откуда S = –
.
Очевидно, что для получения конечного значения усилия S нужно, чтобы знаменатель дроби не был нулевым,
следовательно,
признак необходимой связи по способу замены
связей.
Если для получения системы с простой структурой
требуется произвести замену не одной, а нескольких (n) связей, то признак группы необходимых связей
принимает вид
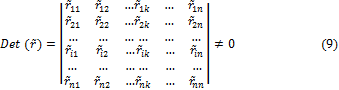
где 
– реакция i-й заменяющей связи от единичного усилия в
удалённой k-й связи (от Sk = 1).
Для систем с W = 0 требования (8) и (9) являются необходимыми и достаточными условиями геометрической неизменяемости.
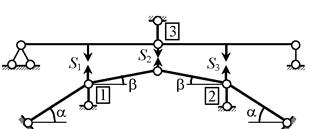
Рис.2.41
Например, в рассматриваемой системе со сложной
структурой (см. рис. 2.39) удаляем одновременно три линейные связи, прикладывая
вместо них реакции S1 , S2 и S3(рис. 2.41), а затем
вводим в систему три заменяющие связи, обозначенные цифрами 1, 2 и 3 в
прямоугольниках. Последовательно задавая S1 = 1, S2 = 1 и S3 = 1, определяем вызываемые ими реакции заменяющих связей и
формируем матрицу :
компоненты второго столбца которой вычислены при tgα=2tgβ. Определитель этой матрицы Det ()
= –3/2 ≠0 – это означает, что
три исследованные связи – необходимые, что является гарантией геометрической
неизменяемости системы. Заметим, что для неё было бы достаточно осуществить
замену лишь одной связи. Читателю предлагается
самостоятельно убедиться в том, что при tgα=-tgβ (неудачная – зигзагообразная геометрия нижней части системы)
получается Det ()
= 0 – признак мгновенной изменяемостисистемы.
И наконец, рассмотрим аналитический признак геометрической неизменяемости. Он формулирует
условие невырожденности системы разрешающих уравнений, формируемых для
вычисления параметров напряжённо-деформированного состояния сооружения. Для линейно
деформируемой системы (физические свойства материала которой
описываются законом Гука, перемещения малы и расчётная схема не изменяется в
процессе деформирования) разрешающие уравнения могут быть представлены в виде
линейных алгебраических уравнений A∙Y+B=0, где Y – вектор неизвестных
силовых факторов и/или перемещений, А – матрица коэффициентов,
зависящая от собственных (геометрических, жесткостных и др.) свойств сооружения, В – вектор
параметров, отражающих влияние заданных воздействий. Единственное решение СЛАУ возможно лишь в
случае, когда Det (A) ≠0 – это и есть необходимое и достаточное аналитическое условие геометрической
неизменяемости системы.
2.6. Понятие о мгновенно изменяемых системах
Расчетная схема любого инженерного сооружения не
должна быть изменяемой или мгновенно изменяемой. Если изменяемость системы
обычно возникает из-за недостатка связей, то мгновенная изменяемость возникает
при их неправильной установке (рис. 2.42, а, г, д, е).
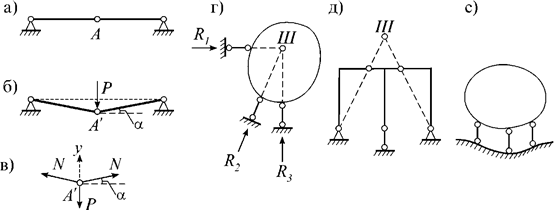
Рис. 2.42
Обнаружить мгновенную изменяемость очень важно
уже на этапе кинематического анализа, так как позволяет вносить коррективы в
расчетную схему сооружения.
В качестве примера рассмотрим балку (рис. 2.42,
а) и выясним, почему же она является мгновенно изменяемой.
1. При действии на эту балку
сосредоточенной силы P ее положение изменится (рис. 2.42, б). Запишем
условие равновесия системы сходящихся сил в точке 
(рис. 2.42, в):
ΣY=N sin𝛼∙2 – P =
0.
Отсюда
Если в этой формуле α=0, т.е. когда стержни AB и BC лежат на одной прямой, то N=∞. Таким образом,
мгновенная изменяемость опасна тем, что усилия в элементах системы могут быть
очень большими.
2. Если в последней формуле примем P=0, внутреннее усилие становится неопределенным: N=0/0.
Этот результат лежит в основе метода нулевой нагрузки. Суть этого метода заключается в следующем:
– удалить все силы, действующие на систему;
– вычислить внутренние усилия. Если они все
(включая и опорные реакции) будут равны нулю, то система неизменяема. Если же
хотя бы одно усилие будет неопределенным (типа 0/0), то данная система является мгновенно изменяемой.
Заключение
Кинематический анализ должен предшествовать
расчёту всегда, когда это практически возможно, – во всяком случае, для систем
со сравнительно небольшим числом элементов. К сожалению, многоэлементные,
особенно пространственные, системы могут иметь достаточно сложную структуру,
трудно поддающуюся исследованию с помощью рассмотренных выше приёмов, требующих
использования геометрических представлений, которые, ко всему прочему, плохо
реализуются в компьютерных программах. В этих случаях может оказаться полезным
использование аналогий с известными решениями, накопленный опыт и т.п. Если же
кинематический анализ сложной системы оказывается неоправданно трудоемким, то
он может не выполняться – при этом попытка автоматизированного компьютерного
расчёта системы с не выявленной заблаговременно геометрической или мгновенной
изменяемостью приведет к тому, что в процессе машинного счета будет обнаружена
невозможность решения вырожденной системы уравнений или будут получены
несоразмерно большие значения усилий (признак систем, близких к мгновенно
изменяемым).
По мере накопления опыта кинематический анализ
может выполняться не обязательно по вышеизложенной полной (двухэтапной) схеме, так
как для систем с простой структурой во многих практических случаях оказывается достаточно только структурного анализа, чтобы сделать заключение о кинематической
природе системы.
Теперь, когда понятны основное предназначение
кинематического анализа (обеспечение функции «входного контроля» расчётной
схемы системы) и методика его выполнения, отметим его прикладное значение:
– во-первых, выявленная в ходе структурного
анализа последовательность образования системы (порядок соединения и добавления
элементов и частей) позволяет для статически определимых систем определить
рациональный порядок расчёта по следующему правилу: расчёт СОС выполняется в порядке, обратном
последовательности её образования. Это значит, что определение реакций начинается со связей, наложенных на диски в
последнюю очередь в процессе синтеза системы, и заканчивается реакциями связей,
введённых на первом шаге образования системы. Иными словами, чем раньше
появилась связь в ходе создания системы из начального набора несвязанных элементов-дисков,
тем позднее в процессе расчёта определяется её реакция;
– во-вторых, с инженерной, практической точки
зрения структурный анализ расчётной схемы сооружения является основой для
назначения правильной последовательности укрупнительной сборки из отдельных
конструктивных элементов и монтажа в проектном положении реальных строительных
конструкций, в результате чего может быть обеспечена неизменяемость возводимого
сооружения на каждом технологическом шаге.