Технический перевод

Операции с матрицами: программирование на C++

Главная

17. Пример расчета арки с затяжкой

Рассмотрим в качестве примера полукруглую арку радиусом R, изображенную на рис.17.1.

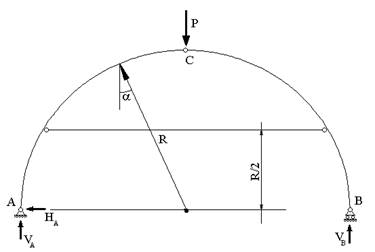
Рис. 17.1

Отбрасываем затяжку (рис.17.1), заменяя ее действие усилием Н, и составляем уравнения равновесия:

Решив эту систему, найдем реакции опор и распор в затяжке:  Этот же результат можно было получить быстрее. Очевидно,  в силу симметрии, а из уравнения  следует H=P.

Внутренние усилия будем определять в сечениях, положение которых определяется углом . В силу симметрии достаточно рассмотреть только одну половину арки. Изгибающий момент в сечениях арки определяется по формуле , причем усилие Н рассматривается как внешняя нагрузка. Определение и  рассмотрено в пункте “Пример расчета арки кругового очертания под действием горизонтальной нагрузки”. Расчеты сводятся в таблицу 17.1.

Таблица 17.1

, градусы
			-ниже затяжки, -выше затяжки
90	0	0	0	0
75	0,034R	0,259R	0	0,017PR
60+0	0,134R	0,5R	0	0,066PR
60-0	0,134R	0,5R	0	0,066PR
45	0,293R	0,707R	-0,207PR	-0,061PR
30	0,5R	0,866R	-0,366PR	-0,116PR
15	0,741R	0,966R	-0,466PR	-0,096PR
0	R	R	-0,5PR	0

Эпюра изгибающего момента приведена на рис. 17.2.

Продольное и перерезывающее усилие определяется по формулам , , причем  - для любого сечения, а  в сечениях, лежащих ниже затяжки,  в сечениях, лежащих выше затяжки. Результаты расчетов приводятся в табл. 17.2.

Эпюры перерезывающей силы и продольного усилия приведены на рис. 17.3 и рис. 17.4.

Таблица 17.2

, градусы
	-ниже затяжки -выше затяжки	-ниже затяжки -выше затяжки
90	0	-0,5P
75	0,129P	-0,483P
60+0	0,250P	-0,433P
60-0	-0,616P	-0,933P
45	-0,353P	-1,061P
30	-0,067P	-1,116P
15	0,224P	-1,095P
0	0,5P	-P

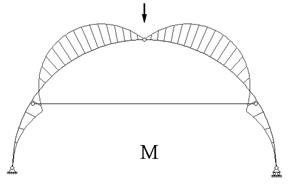
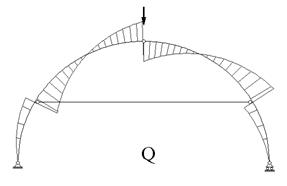
Рис. 17.2                                                              Рис. 17.3

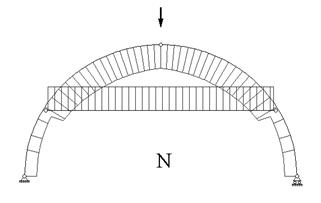
Рис. 17.4