Операции с матрицами:
программирование на C++
15. Пример
расчета арки параболического очертания под действием
вертикальной нагрузки
Рассмотрим арку параболического очертания,
изображенную на рис.15.1.
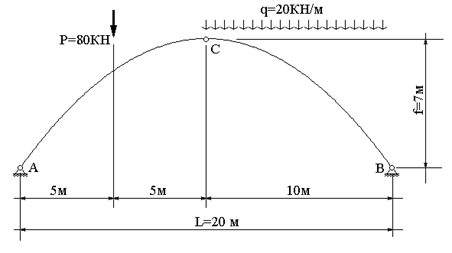
Рис. 15.1
Определим опорные реакции в арке, для чего
запишем систему статических уравнений:
Из второго уравнения
находим:
Далее, из первого
уравнения найдем
И, наконец, найдем распор
Для проверки правильности найденных опорных
реакций составим, например, уравнение моментов сил, действующих справа от
промежуточного шарнира, относительно этого шарнира:
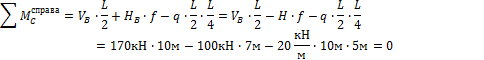
Таким образом, опорные
реакции определены, приступаем к построению эпюры изгибающего момента, для чего
используем формулу 
.
Все расчеты сведем в
таблицу 15.1.
Таблица
15.1
|
x, м |
|
y(x), м |
|
|
|
|
||
|
0 |
0 |
0 |
0 |
|
2,5 |
0 |
3,0625 |
-31,25 |
|
5 |
0 |
5,25 |
25 |
|
7,5 |
-200 |
6,5625 |
-31,25 |
|
10 |
-400 |
7 |
0 |
|
12,5 |
-662,5 |
6,5625 |
56,25 |
|
15 |
-1050 |
5,25 |
75 |
|
17,5 |
-1562,5 |
3,0625 |
56,25 |
|
20 |
-2200 |
0 |
0 |
Покажем, как определяется 
, например, в сечении с координатой x=15 м. Рассматривая часть арки слева от сечения (рис. 15.2),
видим, что изгибающий момент от действия внешних нагрузок складывается из
моментов от действия силы Р с плечом 10 м и действующей на длине 5 м распределенной нагрузки q, равнодействующая которой создает в рассматриваемом сечении
момент с плечом 2,5 м. Оба момента создают растяжение верхних волокон арки в
рассматриваемом сечении, поэтому имеют знак “минус”.
Итак, 
После определения изгибающих моментов от внешней
нагрузки в выбранных сечениях (заполнения столбца 2), приступаем к определению
в этих же сечениях значенийy(x) (столбец 3) и изгибающих моментов в арке (столбец 4). Если во всех
сечениях моменты определяются из рассмотрения равновесия части арки с одной и
той же стороны от сечения (в нашем случае - с левой стороны), последние две
операции для всех сечений выполняются по однотипным формулам. Следовательно,
эти вычисления легко автоматизировать, например, с помощью табличных
процессоров. Если в замке или в опоре арки изгибающий момент в результате
расчета окажется отличным от нуля, то это будет говорить о допущенной ошибке.
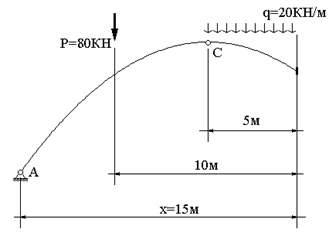
Рис. 15.2
Эпюра изгибающего момента в арке приводится на
рис. 15.3.
Построим теперь эпюры продольного и
перерезывающего усилий, для чего воспользуемся формулами 
и 
. Поскольку горизонтальная составляющая нагрузки
отсутствует, 
при любом х. Все расчеты легко автоматизируются, например, при помощи
табличного процессора. Результаты расчетов сведены в таблицу 15.2.
Таблица
15.2
|
x, м |
кН |
|
|
|
|
|
|
- |
||
|
0 |
110 |
0,950547 |
-17,437 |
-147,635 |
|
2,5 |
110 |
0,809784 |
3,448 |
-148,621 |
|
5-0 |
110 |
0,610726 |
32,769 |
-145,004 |
|
5+0 |
30 |
0,610726 |
-32,769 |
-99,127 |
|
7,5 |
30 |
0,336675 |
-4,719 |
-104,296 |
|
10 |
30 |
0 |
30 |
-100 |
|
12,5 |
-20 |
-0,336675 |
14,158 |
-100,993 |
|
15 |
-70 |
-0,610726 |
0 |
-122,066 |
|
17,5 |
-120 |
-0,809784 |
-10,345 |
-155,862 |
|
20 |
-170 |
-0,950547 |
-17,437 |
-196,459 |
Эпюры перерезывающего и продольных усилий в арке приведены на рис.
15.4 и рис. 15.5.
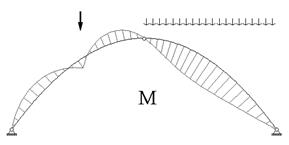
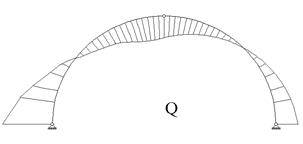
Рис.
15.3 Рис.
15.4
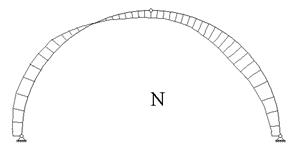
Рис. 15.5
Обратите внимание, что
на оси арки продольное усилие равно распору, а перерезывающее - перерезывающему
усилие в соответствующей балке.