Операции с матрицами:
программирование на C++
13. Примеры расчета фермы на подвижную нагрузку
Пример 1. Рассмотрим ферму, изображенную на рис. 13.1.
Необходимо:
1. Используя теорию линий влияния, определить
усилие в стержне фермы 2-3 от действия неподвижной системы сил, изображенной на
рис.10.1.
2. Определить максимальное и минимальное усилия
в стержне фермы 2-3 при движении по ездовой линии (по горизонтали от узла 1 к
узлу 10) системы из двух сил (рис.13.1).
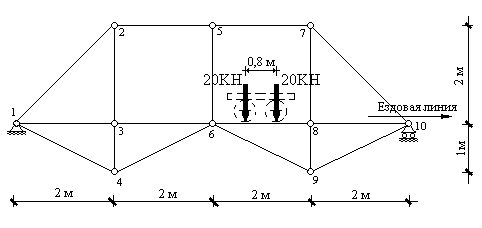
Рис. 13.1
3. Определить усилие от постоянной равномерно
распределенной нагрузки q=10 кН/м, приложенной к поясу фермы,
совпадающему с ездовой линией (рис. 13.2).
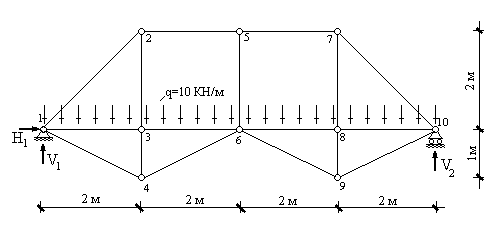
Рис. 13.2
Построим линию влияния для стержня фермы 2-3.
Для этого достаточно определить усилие в этом стержне при различных положениях
единичной силы на ездовой линии.
Если единичная сила находится на расстоянии х от левой опоры, то реакция в последней будет составлять 
, а в правой опоре - 
(рис. 13.3).
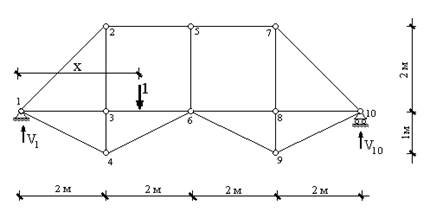
Рис. 13.3
Cоставим уравнения равновесия узла 2 (рис. 13.4):
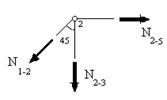
Рис. 13.4
откуда следует, что 
. Поскольку, нагрузки к узлу 2 не приложены,
т.к. он не лежит на ездовой линии, это уравнение справедливо при любом
положении грузов на ней. Для определения 
воспользуемся способом сечений, причем
рассмотрим два случая, когда единичный груз находится слева от панели, в
которой располагается стержень 2-5 (рис. 13.5), и справа от нее (рис. 13.6).
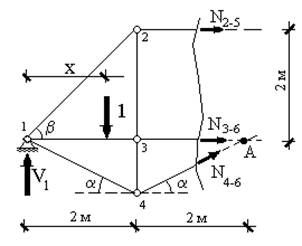
Рис. 13.5
Для первого случая (рис. 13.5) уравнения
равновесия моментов относительно точки А примет вид: 
откуда: 
. Следовательно, при нахождении единичного груза
слева от рассеченной панели (x<2м) 
, а 
.
Согласно этой формуле, при x=0 ордината линии влияния, как и следовало ожидать, равна нулю, а
при x=2м она равна 1/2. По этим точкам строится левая ветвь линии
влияния (до точки С на рис.13.7).
Для второго случая (рис.13.6) из аналогичных
рассуждений получим: 
, откуда: 
. Следовательно, при нахождении единичного груза
справа от рассеченной панели (x>4м) 
, а 
. Таким образом, при x=4м ордината линии влияния равна 1 (точка D на рис.13.7), а на правой опоре, как и следовало ожидать - нулю.
По этим точкам строится правая ветвь линии влияния, и далее передаточная прямая CD. В рассматриваемом случае ее направление, как мы видим, совпадает
с направлением левой ветви линии влияния, а сама линия влияния оказалась
симметричной.
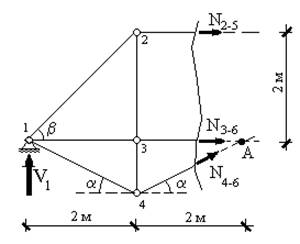
Рис.13.6
Теперь приступим к определению усилий в стержне
2-3.
Для заданной неподвижной узловой нагрузки
(рис.10.1) в соответствии с формулой (4.3) найдем величину усилия в стержне: 
. Этот же ответ был получен нами ранее в разделе
“Пример расчета фермы на неподвижную нагрузку” без использования линий влияния,
что подтверждает правильность проделанных вычислений.
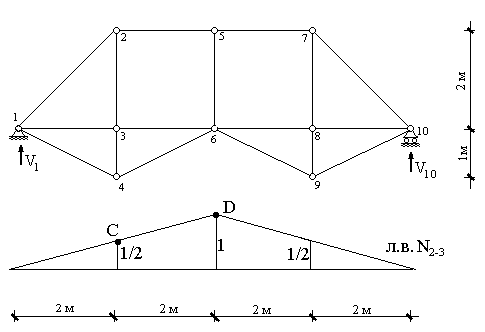
Рис. 13.7
Наиневыгоднейшим положением подвижной системы двух сил на ездовой
линии (рис.13.1) будет положение, когда одна из них находится ровно посередине
пролета фермы (рис.13.8), т.к. в этом случае одна из сил оказывается над
единственной в рассматриваемом случае вершиной линии влияния. Ордината линии
влияния под силой в центре фермы равна 1, ординату под точкой приложения второй
силы легко определить из подобия треугольников: 
, откуда y=0,8 (рис.13.8). В
соответствии с (12.3) усилие в стержне составит 
. В силу симметрии линии влияния, в случае,
когда над ее вершиной в центре пролета фермы окажется не левая, а правая сила,
результат будет тем же.
Построенная линия влияния не имеет отрицательных
ординат, следовательно, при любом положении системы сил на ездовой линии в
стержне будут возникать только растягивающие усилия. Поэтому, максимальным
возможным усилием в стержне 2-3 для
рассматриваемой подвижной нагрузки является 36 кН, минимальным -0 кН.
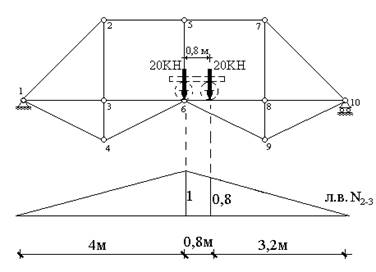
Рис. 13.8
Наконец, определим
усилие в стержне от действия неподвижной равномерно распределенной по всей
длине ездовой линии нагрузки (рис.13.2) q=10 кН/м. Площадь
фигуры, ограниченной линией влияния (рис.13.7) составляет 
. Размерность площади фигуры оказалась такой,
поскольку единичная сила, а следовательно и ординаты линии влияния
продольного усилия не имеют размерности.
Теперь, в соответствии с формулой (12.4),
определим усилие в стержне: 
.
Пример 2. Для фермы, показанной на рис. 13.9, а требуется:
1) определить (аналитически) усилия в стержнях
третьей панели;
2) построить линии влияния усилий в тех же
стержнях;
3) по линиям влияния подсчитать значения усилий
от заданной нагрузки и сравнить их со значениями, полученными аналитически.
Решение.
1. Определяем усилия в стержнях фермы
Расчет начинаем с определения опорных реакций.
Поскольку ферма и нагрузка симметричны, 
.
Для определения усилий в стержнях фермы
применяем метод сечений. Желательно так вести вычисления, чтобы усилие в каждом
стержне определялось независимо от усилий в других стержнях. Это избавляет от
нарастания погрешности расчета и увеличивает его точность. Для этого надлежит
придерживаться следующего порядка:
а) провести разрез фермы, который должен
проходить не больше чем через три стержня, в том числе и через стержень, усилие
в котором требуется определить.
б) отбросить левую или правую часть фермы
(удобнее отбрасывать наиболее нагруженную часть фермы).
в) заменить действие отброшенной части фермы
неизвестными усилиями в разрезанных стержнях; при этом усилия всегда следует
направлять от разреза, предполагая их растягивающими (положительными);
г) составить такое уравнение статики, чтобы, по
возможности, только искомое усилие входило в него как неизвестное.
д) решить уравнение и найти это усилие; если
результат будет со знаком плюс, то стержень растянут; если со знаком минус, то
стержень сжат.
Усилие 
(нижний пояс). Проведем разрез n-n и отбросим правую часть фермы (рис. 13.9, б). Для того чтобы в уравнение
для не вошли усилия 
и 
, следует записать сумму моментов всех сил,
приложенных к оставшейся части фермы, относительно узла 5, в котором
пересекаются линии действия этих усилий. Такая точка называется моментной. Эта
точка всегда находится на пересечении линии действия усилий в двух других
стержнях, попавших в разрез:
Отсюда 
Усилие (верхний пояс). Для нахождения воспользуемся тем же разрезом n-n (рис. 13.9, б), но теперь
моментная точка будет на пересечении линий действия и в узле 6:
Откуда
Усилие (раскос). Для определения вновь воспользуемся разрезом n-n (рис. 13.9, б). Моментная точка находится на пересечении линий действия усилий и в узле А. Проводя из этого узла перпендикуляр на линию действия
искомого усилия (рис. 13.9, г), получим плечо усилия относительно узла 1.
Тогда
Усилие 
(правая стойка). Для нахождения воспользуемся разрезом m-m (рис. 13.9, в). Рассмотрим
равновесие узла 7.
следовательно 
;
Откуда
Усилие 
(левая стойка). Для нахождения воспользуемся разрезом k-k (рис. 13.9, д). Теперь моментная точка будет на пересечении линий действия усилий 
и в узле А, а плечо усилия относительно узла А равно 2d.
, откуда 
2.
Построение линий влияния
2.1. Линии влияния опорных реакций
Линии влияния опорных реакций в балочной ферме (рис. 13.10, а) определяются так же,
как для однопролетной балки. Поэтому линии влияния этих реакций не отличаются
от линий влияния опорных реакций балок (рис. 13.11, б, в).
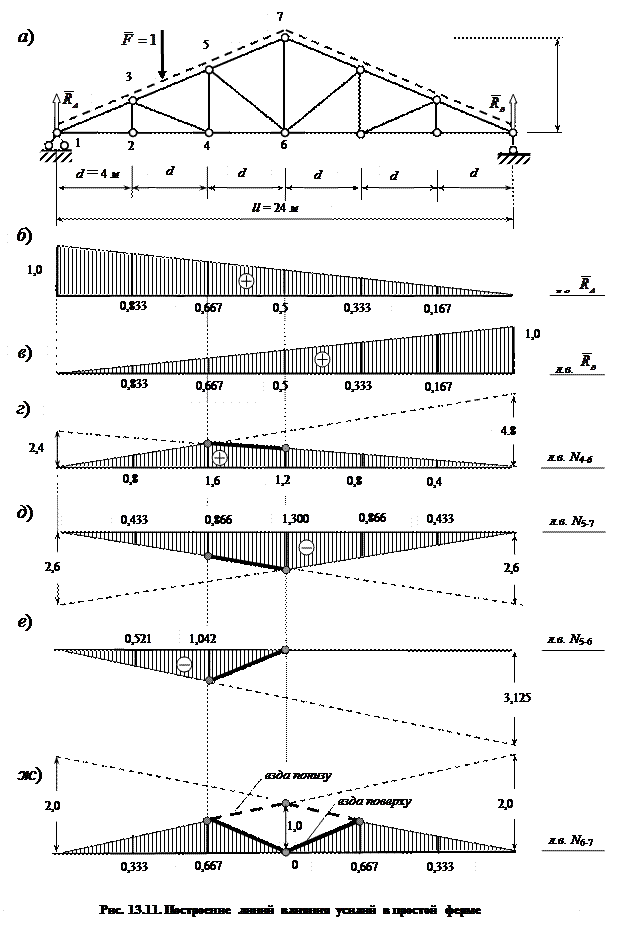
2.2. Линия влияния усилия
Воспользуемся разрезом n-n (рис. 13.10, а). Рассмотрим два
положения единичного груза: справа и слева от разрезанной панели. При положении
груза 
справа от разреза рассматриваем равновесие
левой отсеченной части фермы (рис. 13.10, в) и составляем сумму
моментов относительно моментной точки – узла 5:
Откуда 
т. е. правый участок 
отличается от 
лишь постоянным множителем 2,4.
Строим правую прямую линии влияния 
, откладывая на левой опорной вертикали ординату
2.4 и соединяя ее с нулевой точкой на правой опорной вертикали
(рис. 13.11, г). Полученную правую прямую используем
на участке движения груза справа от разрезанной панели.
При положении груза слева от сечения n–n составляем условие равновесие правой отсеченной
части фермы (рис. 13.10, б):
Откуда 
т. е. левый участок имеет такой же вид, как 
. Умножая ординаты на множитель 4,8, получаем левую прямую (рис. 13.11, г).
При положении груза в пределах разрезанной панели линией
влияния будет передаточная прямая, соединяющая крайние ординаты (передаточные
прямые на рис. 3 показаны жирными
линиями).
2.3. Линия влияния усилия
Вновь воспользуемся разрезом n-n (рис. 13.10, а). Рассмотрим два положения единичного груза:
справа и слева от разрезанной панели. При нахождении груза справа от разреза
рассматриваем равновесие левой отсеченной части
фермы (рис. 2, в) и составляем сумму моментов относительно моментной точки – узла 6:
Откуда 
т. е. правый участок 
отличается от . лишь постоянным множителем 2.6 и знаком
минус. Все ординаты изменяются в 2,6 раз и откладываются от
оси в отрицательном направлении, т. е. вниз (рис. 13.11, д). Построенную таким образом правую прямую используем на участке движения груза
справа от разрезанной панели.
При положении груза слева от разрезанной панели
составляем условие равновесия правой отсеченной части (рис. 13.10, б):
Откуда 
т. е. левый участок отличается от лишь постоянным множителем 2,6 и знаком
минус. Все ординаты изменяются в 2,6 раз и откладываются от
оси в отрицательном направлении т.е. вниз (рис. 3, д). Полученную левую прямую используем на участке движения груза слева от разрезанной панели. В пределах
разрезанной панели соединяем крайние ординаты прямой линией.
Отметим, что в рассмотренных линиях влияния
правая и левая ветви линии влияния пересеклись под моментными точками. Это не
случайно и вытекает из их построения. Эту зависимость будем использовать в
дальнейшем для проверки правильности построения линий влияния.
2.4. Линия влияния усилия
Воспользуемся разрезом n-n (рис. 2, а). При положении
груза справа от разреза рассматриваем равновесие
левой отсеченной части фермы (рис. 2, в) и составляем сумму
моментов относительно моментной точки – узла 1:
Откуда 
, т. е. при грузе , расположенном справа от разреза, усилие равно нулю. Правая прямая линии влияния в
этом случае сливается с осью линии влияния (рис. 13.11, е).
Для построения левой прямой линии влияния
рассмотрим условие равновесия правой отсеченной части фермы (рис.13.10, б):
Откуда 
Это означает, что усилие равно опорной реакции RB, умноженной на (–3,125).
Для построения графика этой зависимости
откладываем на правой опорной вертикали вниз отрезок 3,125 и соединяем его
конец с нулевой точкой на левой опорной вертикали. В пределах разрезанной
панели соединяем крайние точки левой и правой ветвей передаточной прямой.
Построенная таким образом линия влияния изображена на рис. 13.11, е. Отметим, что
вновь правая и левая ветви линии влияния пересеклись под моментной точкой –
узлом 1.
2.5. Линия влияния усилия
Вырежем узел 7 (рис. 13.10, е)
и спроектируем действующие на этот узел силы на горизонтальную ось:
следовательно, .
Спроектируем те же силы на вертикальную ось:
откуда 
.
Таким образом, линия влияния может быть получена умножением всех
ординат линии влияния на коэффициент (-2∙sinα). Линия влияния имеет вид треугольника
(рис. 13.11, ж) с наибольшей ординатой (под узлом 7), равной 1,300(2∙0,3846)=1,000.
Если же груз перемещается по верхнему поясу фермы («езда поверху»), то в тот
момент, когда он окажется в узле 7, уравнение 
примет вид
откуда 
Следовательно, в этом случае ордината на линии
влияния под узлом 7 меньше на единицу, чем
ордината на этой же линии влияния при езде по нижнему поясу, и равна нулю
(сплошная линия на рис. 13.11, ж).
2.6. Вычисление по линиям влияния усилия от заданной постоянной
нагрузки
При вычислении усилий в стержнях от
сосредоточенных сил P=6 kH уравнение (1.1) принимает более простой вид
Тогда
Найденные с помощью линий влияния усилия в
стержнях фермы совпадают с полученными аналитически значениями.