Класс DMATRIX – операции с матрицами на C++

Технический перевод

Главная

Теоретическая механика

Статика

(по материалам сайта engmech.ru)

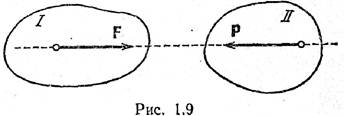
Сила. Система сил. Равновесие абсолютно твердого тела

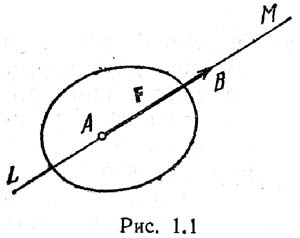
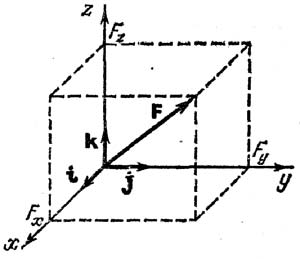
В механике под силой понимается мера механического взаимодействия материальных тел, в результате которого взаимодействующие тела могут сообщать друг другу ускорения или деформироваться (изменять свою форму). Сила— векторной величиной. Она характеризуется численным значением, или модулем, точкой приложения и направлением. Точка приложения силы и ее направление определяют линию действия силы. На рисунке показано, как сила приложена к точке A. Отрезок AB= модулю силы F. Прямая LM называется линией действия силы. В сист. СИ сила изм. в ньютонах (Н). Так же есть 1МН=10⁶Н, 1 кН=10³Н. Существует 2 способа задания силы: непосредственным описанием и векторный (ч-з проекции на оси координат). F= F_xi + F_yj + F_zk , где F_x, F_y, F_z – проекции силы на оси координат, а i, j, k - единичные орты. Абсолютно твёрдое тело— тело в котором расстояние м-ду 2 его точками ост. неизменным независимо от действия на него сил.

Совокупность нескольких сил (F₁, F₂, ... ,F_n) называется системой сил. Если, не нарушая состояния тела, одну систему сил (F₁, F₂, ..., F_n) можно заменить другой системой (Р₁, P ₂ , ... , P_n) и наоборот, то такие системы сил называются эквивалентными. Символически это обозначается следующим образом: ( F ₁ , F ₂ , ... , F_n )~ (Р₁, P ₂ , ... , P_n). Однако, это не означает, что если две системы сил оказывают одинаковое действие на тело они будут эквивалентны. Эквивалентные системы вызывают одинаковое состояние системы. Когда система сил ( F ₁ , F ₂ , ... , F_n ) эквивалентна одной силе R, то R назыв. равнодействующей. Равнодействующая сила может заменить действие всех данных сил. Но не всякая система сил имеет равнодействующую. В инерциальной системе координат выполняется закон инерции. Это означает, в частности, что тело, находящееся в начальный момент в покое, останется пребывать в этом состоянии, если на него не действуют никакие силы. Если абсолютно твердое тело остается в состоянии покоя при действии на него  системы  сил   ( F ₁ , F ₂ , ... , F_n ),   то эта система называется   уравновешенной, или системой сил, эквивалентной нулю: ( F ₁ , F ₂ , ... , F_n )~0. В этом случае говорят, что тело находится в равновесии. В математике два вектора считаются равными, если они параллельны, направлены в одну сторону и равны по модулю. Для эквивалентности двух сил этого недостаточно и из равенства F=Р еще не следует соотношение F~Р. Две силы эквивалентны, если они векторно равны и приложены к одной точке тела.

Аксиомы статики и их следствия

Тело под действием силы приобретает ускорение и не может находиться в покое. Первая аксиома ставит условия, при выполнении которых система сил будет уравновешена.

Аксиома 1. Две силы, приложенные к абсолютно твердому телу, будут уравновешены (эквивалентны нулю) тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Это означает, что если абсолютно твердое тело находится в покое под действием двух сил, то эти силы равны по модулю, действуют по одной прямой и направлены в противоположные стороны. Обратно, если на абсолютно твердое тело действуют по одной прямой в противоположные стороны две равные по модулю силы и тело в начальный момент находилось в покое, то состояние покоя тела сохранится.

На рис. 1.4 показаны уравновешенные силы F₁, F₂ и Р₁, Р₂, удовлетворяющие соотношениям:  (F₁,F₂)~0,  (P₁,Р₂)~0. При решении некоторых задач статики приходится рассматривать силы, приложенные к концам жестких  стержней,   весом которых можно пренебречь, причем известно, что стержни находятся в равновесии. Из сформулированной аксиомы действующие на такой стержень силы направлены вдоль прямой, проходящей через концы стержня, противоположны по направлению и равны друг другу по модулю (рис. 1.5, а). То же самое и в случае, когда ось стержня криволинейная (рис.  1.5, б).

Аксиома 2. Не нарушая состояния абсолютно твердого тела, к нему можно прикладывать или отбрасывать силы тогда и только тогда, когда они составляют уравновешенную систему, в частности, если эта система состоит из двух сил, равных по модулю, действующих по одной прямой и направленных в противоположные стороны. Из этой аксиомы вытекает следствие: не нарушая состояния тела, точку приложения силы можно переносить вдоль линии ее действия.Действительно, пусть сила F_А приложена к точке А (рис. 1.6, а). Приложим в точке В на линии действия силы F_A две уравновешенные силы F_B и F'_B, полагая, что F_B=F_A (рис. 1.6, б). Тогда согласно аксиоме 2 будем иметь F_A~F_A, F_B, F`<sub>B</sub>). Так как силы F<sub>А</sub> и F<sub>B</sub> обра зуют также уравновешенную систему сил (аксиома 1), то согласно аксиоме 2 их можно отбросить (рис. 1.6,в). Таким образом, F<sub>A</sub>~F<sub>A</sub>,F<sub>B</sub>,F`_B)~F_B, или F_A~F_B, что доказывает следствие. Это следствие показывает, что сила, приложенная к абсолютно твердому телу,  представляет собой скользящий вектор. Обе аксиомы и доказанное следствие нельзя применять к деформируемым телам, в частности, перенос точки приложения силы вдоль линии ее действия меняет напряженно-деформированное состояние тела.

Аксиома 3. Не меняя cостояния тела, две силы, приложенные к одной его точке, можно заменить одной равнодействующей силой, приложенной в той же точке и равной их геометрической сумме (аксиома параллелограмма сил). Эта аксиома устанавливает два обстоятельства: 1) две силы F₁ и F₂ (рис. 1.7), приложенные к одной точке, имеют равнодействующую, т. е.  эквивалентны одной  силе (F₁,F₂)~R; 2) аксиома полностью определяет модуль, точку приложения и направление равнодействующей силы R=F₁+F₂.(1.5) Другими словами, равнодействующую R можно построить как диагональ параллелограмма со сторонами, совпадающими с F₁ и F₂. Модуль равнодействующей определится равенством R=(F₁²+F₂²+2F_lF₂cosa)^1/2, где а—угол между данными векторами F₁ и F₂. Третья аксиома применима к любым телам. Вторая и третья аксиомы статики дают возможность переходить от одной системы сил к другой системе, ей эквивалентной. В частности, они позволяют разложить любую силу R на две, три и т. д. составляющие, т. е. перейти к другой системе сил, для которой сила R является равнодействующей. Задавая, например, два направления, которые лежат с R в одной плоскости, можно построить параллелограмм, у которого диагональ изображает силу R. Тогда силы, направленные по сторонам параллелограмма, составят систему, для которой сила R будет равнодействующей (рис. 1.7). Аналогичное построение можно провести и в пространстве. Для этого достаточно из точки приложения силы R провести три прямые, не лежащие в одной плоскости, и построить на них параллелепипед с диагональю, изображающей силу R, и с ребрами, направленными по этим прямым (рис. 1.8).

Аксиома 4 (3-й закон Ньютона). Силы взаимодействия двух тел равны по модулю и направлены по одной прямой в противоположные стороны. Заметим, что силы взаимодействия двух тел не составляют систему уравновешенных сил, так как они приложены к разным телам. Если тело I действует на тело II с силой Р, а тело II действует на тело I с силой F (рис. 1.9), то эти силы равны по модулю (F = Р) и направлены по одной прямой в противоположные стороны, т. е. F= –Р. Если обозначить через F силу, с которой Солнце притягивает Землю, то Земля притягивает Солнце с такой же по модулю, но противоположно направленной силой – F. При движении тела по плоскости к нему будет приложена сила трения Т, направленная в сторону, противоположную движению. Это– сила, с которой неподвижная плоскость действует на тело. На основании четвертой аксиомы тело действует на плоскость с такой же силой, но ее направление будет противоположно силе Т.

На рис. 1.10 показано тело, движущееся вправо; сила трения Т приложена к движущемуся телу, а сила Т'= –Т — к плоскости. Рассмотрим еще покоящуюся систему, изображенную на рис. 1.11, а. Она состоит из двигателя А, установленного на фундаменте В, который в свою очередь находится на основании С. На двигатель и фундамент действуют силы тяжести F₁ и F₂ соответственно. Также действуют силы: F₃– сила действия тела А на тело В (она равна весу тела А); F`з – сила обратного действия тела В на тело А; F<sub>4</sub> – сила действия тел А и В на основание С (она равна суммарному весу тел А и В); F`₄– сила обратного действия основания С на тело В. Эти силы показаны на рис. 1.11, б, в, г.Согласно аксиоме 4 F₃=–F`<sub>3</sub>, F<sub>4</sub>=–F`₄, причем эти силы взаимодействия определяются заданными силами F₁ и F₂. Для нахождения сил взаимодействия необходимо исходить из аксиомы 1. Вследствие покоя тела А (рис. 1.11,6) должно быть F з=–F₁, а значит, F₃=F₁. Точно так же из условия равновесия тела В (рис. 1.11, в) следует F`<sub>4</sub>=–(F<sub>2</sub>+F<sub>3</sub>), т. е. F`₄=–(F₁+F₂) и F₄=F₁+F₂.

Аксиома 5. Равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым. Этой аксиомой пользуются в тех случаях, когда речь идет о равновесии тел, которые нельзя считать твердыми. Приложенные к таким телам внешние силы должны удовлетворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не достаточными. Например, для равновесия абсолютно твердого невесомого стержня необходимо и достаточно, чтобы приложенные к концам стержня силы F и F' действовали по прямой, соединяющей его концы, были равны по модулю и направлены в разные стороны. Эти же условия необходимы и для равновесия отрезка невесомой нити, но для нити они недостаточны— необходимо дополнительно потребовать, чтобы силы, действующие на нить, были растягивающими (рис. 1.12, б), в то время как для стержня они могут быть и сжимающими (рис. 1.12, а).

Рассмотрим случай эквивалентности нулю трех непараллельных сил, приложенных к твердому телу (рис. 1.13, а). Теорема о трех непараллельных силах. Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости, и их линии действия пересекаются в одной точке.Пусть на тело действует система трех сил F₁, F₃ и F₃, причем линии действия сил F₁ и F₂ пересекаются в точке А (рис. 1.13, а). Согласно следствию из аксиомы 2 силы F₁ и F₂ можно перенести в точку А (рис. 1.13, б), а по аксиоме 3 их можно заменить одной силой R, причем (рис. 1.13, в) R=F₁+F₂. Таким образом, рассматриваемая система сил приведена к двум силам R и F₃ (рис. 1.13, в). По условиям теоремы тело находится в равновесии, следовательно, по аксиоме 1 силы R и F₃ должны иметь общую линию действия, но тогда линии действия всех трех сил должны пересекаться в одной точке.

Активные силы и реакции связей

Тело называется свободным, если его перемещения ничем не ограничены. Тело, перемещения которого ограничены другими телами, называется несвободным, а тела, ограничивающие перемещения данного тела,– связями. В точках контакта возникают силы взаимодействия между данным телом и связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Принцип освобождаемоcти: всякое  несвободное тело можно рассматривать как свободное, если действие связей заменить реакциями  их, приложенными  к  данному  телу. В статике полностью определить реакции связей можно с помощью условий или уравнений равновесия тела, которые будут установлены в дальнейшем, но направления их во многих случаях можно определить из рассмотрения свойств связей. 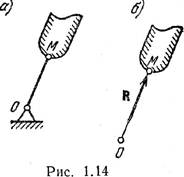В качестве простейшего примера на рис. 1.14, а представлено тело, точка М которого соединена с неподвижной точкой О при помощи стержня, весом которого можно пренебречь; концы стержня имеют шарниры, допускающие свободу вращения. В данном случае для тела связью служит стержень ОМ; стеснение свободы перемещения точки М выражается в том, что она вынуждена находиться на неизменном удалении от точки О. Сила действия на такой стержень должна быть направлена по прямой ОМ, и согласно аксиоме 4 сила противодействия стержня (реакция) R должна быть направлена вдоль той же прямой. Т. 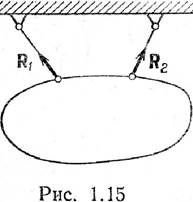о., направление реакции стержня совпадает с прямой ОМ (рис. 1.14, б). Аналогично сила реакции гибкой нерастяжимой нити должна быть направлена вдоль нити. На рис. 1.15 показано тело, висящее на двух нитях, и реакции нитей R₁ и R₂. Силы, действующие на несвободное тело, делят на две категории. Одну категорию образуют силы, не зависящие от связей, а другую– реакции связей. При этом реакции связей носят пассивный характер– они возникают потому что на тело действуют силы первой категории. 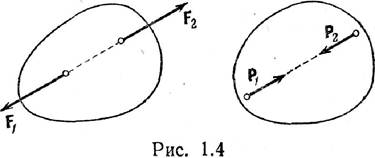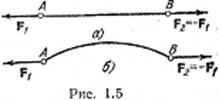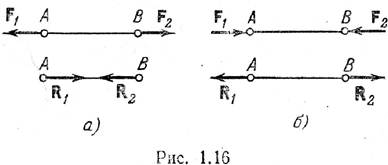Силы, не зависящие от связей, называют активными, а реакции связей– пассивными силами. На рис. 1.16, а вверху показаны две равные по модулю активные силы F₁ и F₂, растягивающие стержень АВ, внизу показаны реакции R₁ и R₂ растянутого стержня. На рис. 1.16, б вверху показаны активные силы F₁ и F₂, сжимающие стержень, внизу показаны реакции R₁ и R₂ сжатого стержня.

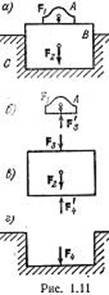
Свойства связей

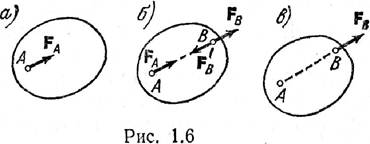
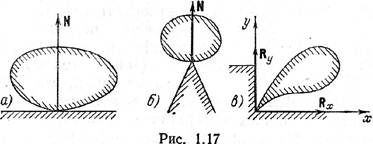
1. Если твердое тело опирается на идеально гладкую (без трения) поверхность, то точка, контакта тела с поверхностью может свободно скользить вдоль поверхности, но не может перемещаться в направлении вдоль нормали к поверхности. Реакция идеально гладкой поверхности направлена по общей нормали к соприкасающимся поверхностям (рис. 1.17, а).Если твердое тело имеет гладкую поверхность и опирается на острие (рис. 1.17, б), то реакция направлена по нормали к поверхности самого тела.Если твердое тело упирается острием в угол (рис. 1.17, в), то связь препятствует перемещению острия как по горизонтали, так и по вертикали. Соответственно реакция R угла может быть представлена двумя составляющими – горизонтальной R_x и вертикальной R_y, величины и направления которых в конечном счете определяются заданными силами.

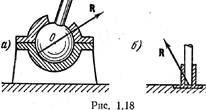
2. Сферическим шарниром называется устройство, изображенное на рис. 1.18, а, которое делает неподвижной точку О рассматриваемого тела. Если сферическая поверхность контакта идеально гладкая, то реакция сферического шарнира имеет направление нормали к этой поверхности. Реакция проходит через центр шарнира О; направление реакции может быть любым и определяется в каждом конкретном случае.

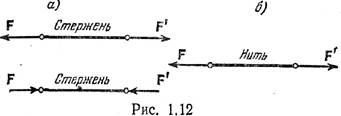
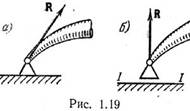
Так же нельзя заранее определить направление реакции подпятника, изображенного на рис. 1.18, б. 3. Цилиндрическая шарнирно-неподвижная опора (рис. 1.19, а). Реакция такой опоры проходит через ее ось, причем направление реакции может быть любым (в плоскости, перпендикулярной оси опоры). 4. Цилиндрическая шарнирно-подвижная опора (рис. 1.19, б) препятствует перемещению закрепленной точки тела по перпендикуляру к плоскости I-I; соответственно реакция такой опоры также имеет направление этого перпендикуляра.

В механических системах, образованных путем сочленения нескольких твердых тел, с внешними связями (опорами) имеются внутренние связи. В этих случаях иногда мысленно расчленяют систему и заменяют отброшенные не только внешние, но и внутренние связи соответствующими реакциями. Силы взаимодействия между отдельными точками данного тела называются внутренними, а силы, действующие на данное тело и вызванные другими телами, называются внешними.

Основные задачи статики

Содержание статики абсолютно твердого тела составляют две основные задачи:

1. Задача о приведении системы сил: как данную систему сил заменить другой, наиболее простой, ей эквивалентной?

2. Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу (или материальной точке), чтобы она была уравновешенной системой?

Вторая задача часто ставится в тех случаях, когда равновесие заведомо имеет место, например, когда заранее известно, что тело находится в равновесии, которое обеспечивается связями, наложенными на тело. При этом условия равновесия устанавливают зависимость между всеми силами, приложенными к телу. С помощью этих условий удается определить опорные реакции. Нужно иметь в виду, что определение реакций связей (внешних и внутренних) необходимо для последующего расчета прочности конструкции.

В более общем случае, когда рассматривается система тел, имеющих возможность перемещаться друг относительно друга, одной из основных задач статики является задача определения возможных положений равновесия.

Приведение системы сходящихся сил к равнодействующей

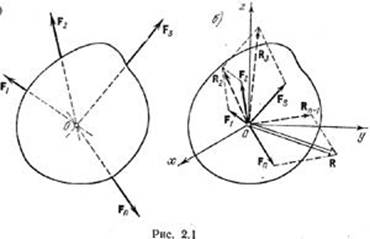
Силы называются сходящимися, если линии действия всех сил, составляющих систему, пересекаются в одной точке. Докажем теорему: Система сходящихся сил эквивалентна одной силе (равнодействующей), которая равна сумме всех этих сил и проходит через точку пересечения их линий действия. Пусть задана система сходящихся сил F₁, F₂, F₃, ..., F_n, приложенных к абсолютно твердому телу (рис. 2.1, а). Перенесем точки приложения сил по линиям их действия в точку пересечения этих линий (21, б). Получили сист сил, прил к одной точке. Она эквивалентна заданной. Сложим F₁ и F₂, получим их равнодействующую: R₂=F₁+F₂. Сложим R₂ с F₃: R₃=R₂+F₃=F₁+F₂+F₃. Сложим F₁+F₂+F₃+…+F_n=R_n=R=åF_i. 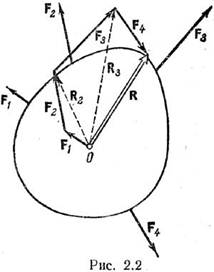Ч.т.д. Вместо параллелограммов можно построить силовой многоугольник. Пусть система состоит из 4 сил (рис 2.2.). От конца вектора F₁ отложим вектор F₂. Вектор, соединяющий начало О и конец вектора F₂, будет вектором R₂. Далее отложим вектор F₃ помещая его начало в конце вектора F₂. Тогда мы получим вектор R₈, идущий от точки О к концу вектора F₃. Точно так же добавим вектор F₄; при этом получим, что вектор, идущий от начала первого вектора F₁ к концу вектора F₄, является равнодействующей R. Такой пространственный многоугольник называется силовым. Если конец последней силы не совпадает с началом  первой силы, то силовой многоугольник наз разомкнутым. Если для нахождения равнодействующей исп прав геометр, то этот способ наз геометрическим.

Больше пользуются аналитическим способом для определения равнодействующей. Проекция суммы векторов на некоторую ось равна сумме проекций на ту же ось слагаемых векторов, получим R_x=åF_kx=F_1x+F_2x+…+F_nx; R_y=åF_ky=F_1y+F_2y+…+F_ny; R_z=åF_kz=F_1z+F_2z+…+F_nz; где F_kx, F_ky, F_kz– проекции силы F_k на оси, а R_x, R_y, R_z– проекции равнодействующей на те же оси. Проекции равнодействующей системы сходящихся сил на координатные оси равны алгебраическим суммам проекций этих сил на соответствующие оси. Модуль равнодействующей R равен: R=(R_x²+R_y²+R_z²)^1/2. Направляющие косинусы равны: cos(x,R)=R_x/R, cos(y,R)=R_y/R, cos(z,R)=R_z/R. Если силы распол в пл-ти то всё аналогично, отсутствует ось Z.

Условия равновесия системы сходящихся сил

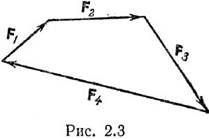
(F₁, F₂, ... ,F_n)~R => для равновесия тела, находящегося под действием системы сходящихся сил, необходимо и достаточно, чтобы их равнодействующая равнялась нулю: R = 0. Следовательно, в силовом многоугольнике уравновешенной системы сходящихся сил конец последней силы должен совпадать с началом первой силы; в этом случае говорят, что силовой многоугольник замкнут (рис. 2.3). Это условие используется при графическом решении задач для плоских систем сил. Векторное равенство R=0 эквивалентно трем скалярным равенствам: R_x=åF_kx=F_1x+F_2x+…+F_nx=0; R_y=åF_ky=F_1y+F_2y+…+F_ny=0; R_z=åF_kz=F_1z+F_2z+…+F_nz=0; где F_kx, F_ky, F_kz– проекции силы F_k на оси, а R_x, R_y, R_z– проекции равнодействующей на те же оси. Т. е. для равновесия сходящейся системы сил необходимо и достаточно равенства нулю алгебраических сумм проекций всех сил данной системы на каждую из координатных осей. Для плоской системы сил пропадает условие, связанное с осью Z. Условия равновесия позволяют проконтролировать, находится ли в равновесии заданная система сил.

Сложение двух параллельных сил

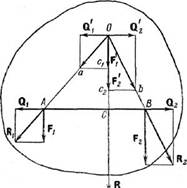
1) Пусть параллельные и одинаково направленные силы F₁ и F₂ приложены к точкам А и В тела и нужно найти их равнодействующую (рис. 3.1). Приложим к точкам А и В равные по модулю и противоположно направленные силы Q₁ и Q₂ (их модуль может быть любым); такое добавление можно делать на основании аксиомы 2. Тогда в точках А и В мы получим две силы  R₁ и R₂: R₁~(F₁, Q₁) и R₂~(F₂, Q₂). Линии действия этих сил пересекаются в некоторой точке О. Перенесем силы R₁ и R₂ в точку О и разложим  каждую на составляющие: R₁~(F₁’, Q₂’) и R₂~(F₂’, Q₂’). Из построения видно, что Q₁’=Q₁ и Q₂’=Q₂, следовательно, Q₁’= –Q₂’и две эти силы согласно аксиоме 2 можно отбросить. Кроме того, F₁’=F₁, F₂’=F₂. Силы F₁’ и F₂’ действуют по одной прямой, и их можно заменить одной силой R = F₁ + F₂, которая и будет искомой равнодействующей. Модуль равнодействующей равен R = F₁ + F₂. Линия действия равнодействующей параллельна линиям действия F₁ и F₂. Из подобия треугольников Оас₁ и ОАС, а, также Оbс₂ и ОВС получим соотношение: F₁/F₂=BC/AC. Этим соотношением определяется точка приложения равнодействующей R. Система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, параллельную этим силам, причем ее модуль равен сумме модулей этих сил.

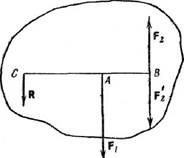
2) Пусть на тело действ две парал силы, направл в разные стор и не равные по модулю. Дано: F₁, F₂; F₁>F₂.

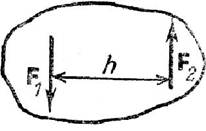
Пользуясь формулами R = F₁ + F₂ и F₁/F₂=BC/AC, можно силу F₁ разложить на две составляющие, F'₂ и R, направленные в сторону силы F₁. Сделаем это так, чтобы сила F'₂оказалась приложенной к точке В, и положим F'₂ = –F₂. Таким образом, (F_l, F₂)~(R, F'₂, F₂). Силы F₂, F₂’ можно отбросить как эквивалентные нулю (аксиома 2), следовательно, (F₁,F₂)~R, т. е. сила R и является равнодействующей. Определим силу R, удовлетворяющую такому разложению силы F₁. Формулы R = F₁ + F₂ и F₁/F₂=BC/AC дают R+F₂’=F₁, R/F₂=AB/AC (*). Отсюда следует R = F₁–F₂’= F₁ + F₂, и так как силы F_t и F₂ направлены в разные стороны, то R=F₁–F₂. Подставив это выражение во вторую формулу (*), получим после простых преобразований F₁/F₂=BC/AC. соотношением определяется точка приложения равнодействующей R. Две не равные по модулю противоположно направленные параллельные силы имеют равнодействующую, параллельную этим силам, а ее модуль равен разности модулей этих сил.

3) Пусть на тело действуют две парал, равных по модулю, но противоп по напр силы. Эта система назыв парой сил и обозначается символом (F₁, F₂). Предположим, что модуль F₂ постепенно возрастает, приближаясь к значению модуля F₁. Тогда разность модулей будет стремиться к нулю, а система сил (F₁, F₂)– к паре. При этом |R|Þ0, а линия ее действия– удаляться от линий действия этих сил. Пара сил представляет собой неуравновешенную систему, которая не может быть заменена одной силой. Пара сил не имеет равнодействующей.

Момент силы относительно точки и оси. Момент пары сил

Моментом силы относительно  точки (центра) называется вектор, численно равный произведению модуля силы на плечо, т. е. на кратчайшее расстояние от указанной точки до линии действия силы. Он направлен перпендикулярно плоскости, проходящей через выбранную точку и линию действия силы. Если мом силы по часов стрелки, то момент отрицательный, а если против, то положительный. Если O— точка, относ кот находится момент силы F, то момент силы обозначается символом М_о(F). 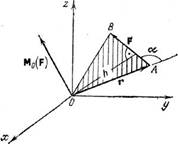Если точка приложения силы F определяется радиусом-вектором r относительно О, то справедливо соотношение М_о(F)=г х F. (3.6) Т.е. момент силы равен векторному произведению вектора r на вектор F. Модуль   векторного   произведения   равен М_о(F)=rF sin a=Fh, (3.7) где h — плечо силы. Вектор М_о(F) направлен перпендикулярно плоскости, проходящей через векторы r и F, и против часовой стрелки. Таким образом, формула (3.6) полностью определяет модуль и направление момента силы F. Формулу (3.7) можно записать в виде M_O(F)=2S, (3.8) где S– площадь треугольника ОАВ. Пусть x, у, z — координаты точки приложения силы, a F_x, F_y, F_z — проекции силы на координатные оси. Если т. О нах. в начале координат, то момент силы:

Значит, проекции момента силы на координатные оси определяются ф-ми: M_ox(F)=yF_z–zF_y, M_oy(F)=zF_x–xF_z, M_oz(F)=xF_y–yF_x (3.10).

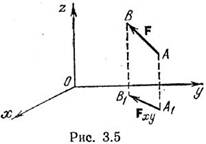
Введем понятие проекции силы на плоскость. Пусть дана сила F и нек-ая пл-ть. Опустим из начала и конца вектора силы перпендикуляры на эту плоскость (рис. 3.5). Проекцией силы на плоскость называется вектор, начало и конец которого совпадают с проекцией начала и проекцией конца силы на эту  плоскость. Проекцией силы F на пл-ть xOy будет F_xy. Момент силы F_xy отн. т. О (если z=0, F_z=0) будет M_o(F_xy)=(xF_y–yF_x)k. Этот момент направлен вдоль оси г, а его проекция на ось z в точности совпадает с проекцией на ту же ось момента силы F относительно точки О.Т.е, M_Oz(F)=М_Оz(F_xy)=xF_y–yF_x. (3.11). Тот же результат можно получить, если спроектировать силу F на любую другую плоскость, параллельную плоскости хОу. При этом точка пересечения оси с плоскостью будет уже иной (обозначим О₁). Однако все входящие в правую часть равенства (3.11) величины х, у, F_x, F_y останутся неизменными: M_Oz(F)=M_Olz(F_xy). Проекция момента силы относительно точки на ось, проходящую через эту точку, не зависит от выбора точки на оси. Вместо M_Oz(F) запишем M_z(F). Эта проекция момента называется моментом силы относительно оси z. Перед вычислениями силу F проецируют на пл-ть, перп оси. М_z(F)=М_z(F_xy)=±F_xyh (3.12). h- плечо. Если по часовой стрелки, то +, против –. Для вычисления мом. сил нужно: 1) выбрать на оси произвольную точку и построить плоскость,  перпендикулярную оси; 2)  спроектировать   на эту плоскость силу; 3)  определить плечо проекции силы h. Момент силы относительно оси равен произведению модуля проекции силы на ее плечо, взятому с соответствующим знаком. Из (3.12) следует, что момент силы относительно оси равен нулю: 1) когда проекция силы на плоскость, перпендикулярную оси, равна нулю, т. е. когда сила и ось параллельны; 2) когда плечо проекции h равно нулю, т. е. когда линия действия силы пересекает ось. Или: момент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось находятся в одной плоскости.

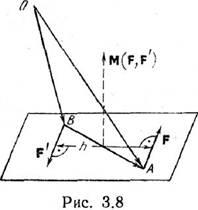
Введем понятие момента пары. Найдем, чему равна сумма моментов сил, составляющих пару, относительно произвольной точки. Пусть О — произвольная точка пространства (рис. 3.8),  a F и F' — силы,  составляющие пару. Тогда М_о(F)=ОАxF,    М_о(F')= OBxF', откуда М_о(F)+М_о(F')=ОАxF+OBxF', но так как F'=–F, то M₀(F)+M₀(F')=OAxF–ОBхF=(ОА– OB)xF. Принимая  во  внимание равенство  ОА–ОВ=ВА,окончательно находим: M₀(F)+M₀(F')=BAхF. Т.е., сумма моментов сил, составляющих пару, не зависит от положения точки, относительно которой берутся моменты. Векторное произведение ВАxF называется моментом пары. Обозначается момент пары символом М(F,F'), причем М(F,F')=BAxF=АВxF', или, М=ВАхF=АВхF'. (3.13). Момент пары представляет собой вектор, перпендикулярный плоскости пары, равный по модулю произведению модуля одной из сил пары на плечо пары (т. е. на кратчайшее расстояние между линиями действия сил, составляющих пару) и направленный в ту сторону, откуда «вращение» пары видно происходящим против хода часовой стрелки. Если h – плечо пары, то М(F,F')=hF. Чтобы пара сил сост уравновеш сист необх: чтобы момент пары=0, либо плечо=0.

Теоремы о парах

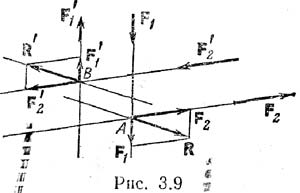
Теорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар. Для док–ва рассмотрим две пары (F₁, F`<sub>1</sub>) и (F<sub>2</sub>, F`₂) (рис. 3.9) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по   аксиоме 3, получим R=F₁+F₂ и R'=F`<sub>1</sub>+F`₂,  но F'₁=–F₁ и F`<sub>2</sub>=–F<sub>2</sub>. Следовательно, R=–R', т. е. силы R и R' образуют пару. Момент этой пары: М=М(R, R')=ВАxR=BAx(F<sub>1</sub>+F<sub>2</sub>)=ВАxF<sub>1</sub>+ВАxF<sub>2</sub>. (3.14). При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пары не меняются, следовательно, не меняется и момент пары. Значит, ВАхF<sub>1</sub>=M(F<sub>1</sub>, F'<sub>1</sub>)=M<sub>1</sub>, ВАxF<sub>2</sub>=M(F<sub>2</sub>, f`₂)=M₂, и формула (З.14) примет вид M=M₁+M₂, (3.15) ч.т.д. Сделаем два  замечания. 1. Линии   действия   сил, составляющих   пары,  могут оказаться параллельными. Теорема остается справедливой и в этом случае. 2. После сложения  может  получиться, что М(R,R')=0; на основании замечания1 из этого следует, что совокупность двух пар (F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂)~0.

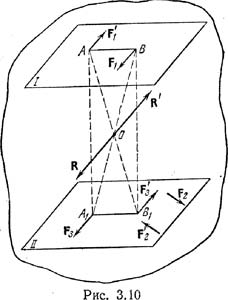
Теорема 2. Две пары, имеющие равные моменты, эквивалентны. Пусть на тело в плоскости I действует пара (F₁,F`<sub>1</sub>) с моментом M<sub>1</sub>. Покажем, что эту пару можно заменить другой парой (F<sub>2</sub>, F`₂), расположенной в плоскости II, если только ее момент М₂ равен М₁. Заметим, что плоскости I и II должны быть параллельны, в частности, они могут совпадать. Действительно, из параллельности моментов M₁, и М₂ следует, что плоскости действия пар, перпендикулярные моментам, также параллельны. Введем в рассмотрение новую пару (F₃, F`<sub>3</sub>) и приложим ее вместе с парой (F<sub>2</sub>, F`₂) к телу, расположив обе пары в плоскости II. Для этого согласно аксиоме 2 нужно подобрать пару (F₃, F`<sub>3</sub>) с моментом М<sub>3</sub> так, чтобы приложенная система сил (F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>) была уравновешена. Положим F<sub>3</sub>=–F`₁ и F`<sub>3</sub>=–F<sub>1</sub> и совместим точки приложения этих сил с проекциями А<sub>1</sub> и B<sub>1</sub> точек  А и В на плоскость II (см. рис. 3.10). В соответствии с построением будем иметь: М<sub>3</sub>=–M<sub>1</sub> или, учитывая, что М<sub>1</sub>=М<sub>2</sub>, М<sub>2</sub>+М<sub>3</sub> = 0, получим (F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>)~0. Т.о., пары (F<sub>2</sub>, F`₂) и (F₃, F`<sub>3</sub>) взаимно уравновешены и присоединение их к телу не нарушает его состояния (аксиома 2), так что (F<sub>1</sub>, F`₁)~(F₁, F`<sub>1</sub>, F<sub>2</sub>, F`₂, F₃, F`<sub>3</sub>). (3.16). С другой стороны, силы F<sub>1</sub> и F<sub>3</sub>, а также F`₁ и F`<sub>3</sub> можно сложить по правилу сложения параллельных сил, направленных в одну сторону. Они равны по модулю, поэтому их равнодействующие R и R' должны быть приложены в точке пересечения диагоналей прямоугольника ABB<sub>1</sub>A<sub>1</sub>, кроме того, они равны по модулю и направлены в противоположные стороны. Это означает, что они составляют систему, эквивалентную нулю.  Итак, (F<sub>1</sub>, F`₁, F₃, F`<sub>3</sub>)~(R, R')~0. Теперь можем записать (F<sub>1</sub>, F`₁, F₂, F`<sub>2</sub>, F<sub>3</sub>,F`₃)~(F₂, F`<sub>2</sub>).(3.17). Сравнивая соотношения (3.16) и (3.17), получим (F<sub>1</sub>, F`₁)~(F₂, F`₂), ч.т.д. Из этой теоремы следует, что пару сил можно перемещать и поворачивать в плоскости ее действия, переносить в параллельную плоскость; в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F₁h₁=F₂h₂).

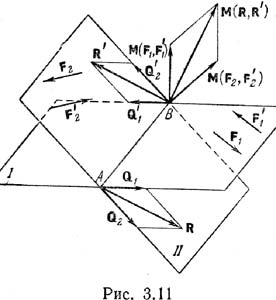
Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар. Пусть пары (F₁, F`<sub>1</sub>) и (F<sub>2</sub>, F`₂) расположены в пересекающихся плоскостях I и II соответственно. Пользуясь следствием теоремы 2, приведем обе пары к плечу АВ (рис. 3.11), расположенному на линии пересечения плоскостей I и II. Обозначим трансформированные пары через (Q₁, Q`<sub>1</sub>) и (Q<sub>2</sub>, Q`₂). При этом должны выполняться равенства: M₁=M(Q₁, Q`<sub>1</sub>)=M(F<sub>1</sub>, F`₁) и M₂=M(Q₂, Q`<sub>2</sub>)=M(F<sub>2</sub>, F`₂). Сложим по аксиоме 3 силы, приложенные в точках А и В соответственно. Тогда получим R=Q₁+Q₂ и R'=Q`<sub>1</sub>+Q`₂. Учитывая, что Q`<sub>1</sub>=–Q<sub>1</sub> и Q`₂= –Q₂, получим: R=–R'. Т.о., мы доказали, что система двух пар эквивалентна одной паре (R, R'). Найдем  момент М этой пары. М(R, R')=ВАxR, но R=Q₁+Q₂ и М(R, R')=ВАх(Q₁+Q₂)=BAxQ₁+BAxQ₂=M(Q₁, Q`<sub>1</sub>)+M(Q<sub>2</sub>, Q`₂)=M(F₁, F'₁)+M(F₂, F`₂), или M=M₁+M₂, т. е. теорема доказана.

Вывод: момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. Для деформируемых тел теория пар неприменима.

Приведение системы пар к простейшему виду. Равновесие системы пар

Пусть дана система п пар (F₁,F₁<sup>`</sup>),(F<sub>2</sub>,F`₂) ..., (F_n,F`<sub>n</sub>), как угодно  расположенных в пространстве, моменты которых равны M<sub>1</sub>, М<sub>2</sub> ..., М<sub>n</sub>. Первые две пары можно заменить одной парой (R<sub>1</sub>,R`₁) с моментом M*₂:М*₂=M₁+М₂. Полученную пару (R₁, R`<sub>1</sub>) сложим с парой (F<sub>3</sub>, F`₃), тогда получим новую пару (R₂, R`₂) с моментом М*₃: М*₃=М*₂+М₃=М₁+М₂+М₃. Продолжая и дальше последовательное сложение моментов пар, мы получим последнюю результирующую пару (R, R') с моментом M=M₁+M₂+...+M_n=åM_k. (3.18). Cистема пар приводится к одной паре, момент которой равен  сумме  моментов всех  пар. Теперь легко решить вторую задачу статики, т. е. найти условия равновесия тела, на которое действует система пар. Для того чтобы система пар была эквивалентна нулю, т. е. приводилась к двум уравновешенным силам, необходимо и достаточно, чтобы момент результирующей пары был равен нулю. Тогда из формулы (3.18) получим следующее условие равновесия в векторном виде: М₁ + М₂ + М₃ + ... + М_n=0. (3.19).

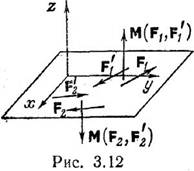
В проекциях на координатные оси уравнение (3.19) дает три скалярных уравнения. Условие равновесия (3.19) упрощается, когда все пары лежат в одной плоскости. В этом случае все моменты перпендикулярны этой плоскости, и поэтому уравнение (3.19) достаточно спроектировать только на одну ось, например ось, перпендикулярную плоскости пар. Пусть это будет ось z (рис. 3.12). Тогда из уравнения  (3.19) получим: М_1Z+М_2Z+...+М_nZ=0. При этом ясно, что М_Z=М, если вращение пары видно с положительного направления оси z против хода часовой стрелки, и М_Z= –М при противоположном направлении вращения. Оба эти случая представлены на рис. 3.12.

Лемма о параллельном переносе силы

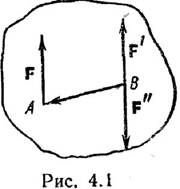
Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F~(F, F', F"), так как (F',F")~0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=M_B(F). Таким образом, лемма о параллельном переносе силы доказана.

Основная теорема статики

Пусть дана произвольная система сил (F₁, F₂,..., F_n). Сумму этих сил F=åF_k называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса.

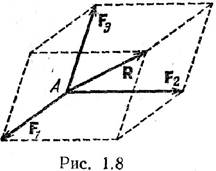
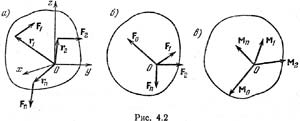
Основная теорема статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. Пусть О — центр приведения, принимаемый за начало координат, r₁,r₂, r₃,…, r_n–соответствующие радиусы-векторы точек приложения сил F₁, F₂, F₃, ...,F_n, составляющих данную систему сил (рис. 4.2, а). Перенесем силы F₁, F_a, F₃, ..., F_n в точку О. Сложим эти силы как сходящиеся; получим одну силу: F_о=F₁+F₂+…+F_n=åF_k, которая равна главному вектору (рис. 4.2, б). Но при последовательном переносе сил F₁, F₂,..., F_n в точку О мы получаем каждый раз соответствующую пару сил (F₁, F”₁), (F₂,F”₂),...,(F_n, F"_n).Моменты этих пар соответственно равны моментам данных сил относительно точки О: М₁=М(F₁,F”₁)=r₁ x F₁=М_о(F₁), М₂=М(F₂, F”₂)=r₂ x F₂=М_о(F₂), …, М_п=М(F_n, F"_n)=r_n x F_n=М_о(F_n). На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т. е. равен главному моменту, так как согласно формулам (3.18) и (4.1) имеем (рис. 4.2, в) М₀=М₁+М₂+...+М_n=М_о(F₁)+М_о(F₂)+…+ М_о(F_n)==åМ_о(F_k)=år_k x F_k. Систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой F_o=åF_k (4.2) и парой сил с моментом M₀=åM₀(F_k)=år_k x F_k. (4.3). В технике очень часто проще задать не силу или пару, а их моменты. Например, в характеристику электромотора входит не сила, с которой статор действует на ротор, а вращающий момент.

Условия равновесия пространственной системы сил

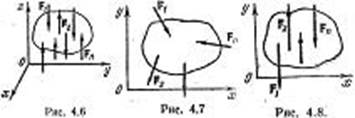
Теорема. Для равновесия пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы равнялись нулю. Достаточность: при F_o=0 система сходящихся сил, приложенных в центре приведения О, эквивалентна нулю, а при М_о=0 система пар сил эквивалентна нулю. Следовательно, исходная система сил эквивалентна нулю. Необходимость: Пусть данная система сил эквивалентна нулю. Приведя систему к двум силам, заметим, что система сил Q и Р (рис. 4.4) должна быть эквивалентна нулю, следовательно, эти две силы должны иметь общую линию действия и должно выполняться рав-во Q=–Р. Но это может быть, если линия действия силы Р проходит через точку О, т. е. если h=0. А это значит, что главный момент равен нулю (М_о=0). Т.к. Q+Р=0, a Q=F_o+P', то F_o+P'+P=0, и, следовательно, F_o = 0. Необх и дост усл равнов пространственной сист сил им вид: F_o=0, M_o=0 (4.15),

или,  в проекциях на  координатные оси, Fox=åF_kx=F_1x+F_2x+…+F_nx=0; F_Oy=åF_ky=F_1y+F_2y+...+F_ny=0; F_oz=åF_kz=F_1z+F_2z+…+F_nz=0 (4.16).   M_Ox=åM_Ox(F_k)=M_Ox(F₁)+М_ox (F₂)+...+M_Ox(F_n)=0, M_Oy=åM_Oy(F_k)=M_oy(F₁)+M_oy(F₂)+…+M_oy (F_n)=0, М_oz=åМ_Оz(F_k)=М_Оz(F₁)+M_oz (F₂)+...+М_oz(F_n)=0. (4.17)

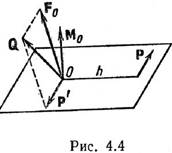
Т.о. при решении задач имея 6 ур-ий можно найти 6 неизвестных. Замечание: пару сил нельзя привести к равнодействующей. Частные случаи: 1) Равновесие пространственной системы параллельных сил. Пусть ось Z параллельна линиям действ силы (рис 4.6), тогда проекции сил на x и y равны 0 (F_kx=0 и F_ky=0), а остаётся только F_oz. А что касается моментов, то остаются только M_ox и M_oy, а M_oz отсутствует. 2) Равновесие плоской системы сил. 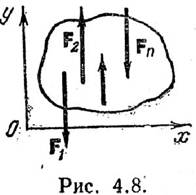Остаются ур-я F_ox, F_oy и момент M_oz (рис 4.7). 3) Равновесие плоской системы параллельных сил. (рис. 4.8). Остаются только 2 ур-я: F_oy и M_oz.При составлении ур-ий равновесия за центр привидения может быть выбрана любая точка.

Привидение плоской системы сил к простейшему виду

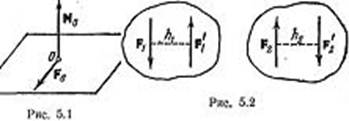
Рассмотрим систему сил (F_1, F₂,..., F_n), расположенных в одной плоскости. Совместим с плоскостью расположения сил систему координат Оху и, выбрав ее начало в качестве центра приведения, приведем рассматриваемую систему сил к одной силе F₀=åF_k, (5.1) равной главному вектору, и к паре сил, момент которой равен главному моменту M₀=åM₀(F_k), (5.2) где М_о(F_k)– момент силы F_k относительно центра приведения О. Так как силы распол в одной пл-ти, то сила F_o также лежит в этой плоскости. Момент пары М_о направлен перпендикулярно этой плоскости, т.к. сама пара распол в пл-ти действия рассматриваемых сил. Т.о., для плоской системы сил главный вектор и главный момент всегда перпендикулярны друг другу (рис. 5.1). Момент полностью характеризуется алгебраической величиной M_z, равной произведению плеча пары на величину одной из сил, составляющих пару, взятой со знаком плюс, если «вращение-» пары происходит, против хода часовой стрелки, и со знаком минус, если оно происходит по ходу часовой стрелки. Пусть, например, даны две пары, (F₁, F`<sub>1</sub>) и (F<sub>2</sub>, F`₂) (рис. 5.2); тогда согласно данному определению имеем M_z(F₁,F`<sub>1</sub>)=h<sub>1</sub>F<sub>1</sub>, M<sub>Z</sub>(F<sub>2</sub>,F'<sub>2</sub>)=-h<sub>2</sub>F<sub>2</sub>. Моментом силы относительно точки будем называть алгебраическую величину, равную проекции вектора момента силы относительно этой точки на ось, перпендикулярную плоскости, т. е. 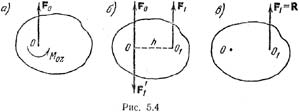равную произведению модуля силы на плечо, взятому с соответствующим знаком. Для случаев, изображенных на рис. 5.3, а и б, соответственно будет M<sub>oz</sub>(F<sub>1</sub>)=hF<sub>1</sub>, M<sub>oz</sub>(F<sub>2</sub>)=–hF<sub>2</sub> (5.4). Индекс z в формулах (5.3) и (5.4) сохранен для того, чтобы указать на алгебраический характер моментов. Модули момента пары и момента силы обозначаются следующим образом: М(F,F')=| М<sub>z</sub>(F,F`)|, М_о(F)=|М_Оz(F)|. Получим, M_oz=åM_oz(F_z). Для аналитического определения главного вектора применяются формулы: F_ox=åF_kx=F_1x+F_2x+…+F_nx, F_oy=åF_ky=F_1y,+F_2y+…+F_ny, F_o=(F²_ox+F²_oy)^1/2=([åF_kx]²+[åF_ky]²)^1/2 (5.8); cos(x, F_o)=F_ox /F_o, cos(y, F_o)=F_Oy/F_o.(5.9). А главный момент равен М_Оz=åM_Oz(F_k)=å(x_kF_ky–y_kF_kx), (5.10) где x_k, y_k– координаты точки приложения силы F_k.

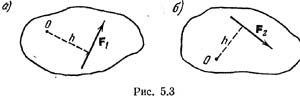
Докажем, что если главный вектор плоской системы сил не равен нулю, то данная система сил эквивалентна одной силе, т. е. приводится к равнодействующей. Пусть Fo≠0, МОz ≠0 (рис. 5.4, а). Дуговая стрелка на рис. 5.4, а символически изображает пару с моментом MOz. Пару сил, момент которой равен главному моменту, представим в виде двух сил F1 и F`1, равных по модулю главному вектору Fo, т. е. F1=F`1 =Fo. При этом одну из сил (F`1), составляющих пару, приложим к центру приведения и направим в сторону, противоположную направлению силы Fo (рис. 5.4, б). Тогда система сил Fo и F`1 эквивалентна нулю и может быть отброшена. Следовательно, заданная система сил эквивалентна единственной силе F1 приложенной к точке 01; эта сила и является равнодействующей. Равнодействующую будем обозначать буквой R, т.е. F1=R. Очевидно, что расстояние h от прежнего центра приведения О до линии действия равнодействующей можно найти из условия |MOz|=hF1 =hFo, т.е. h=|MOz|/Fo. Расстояние h нужно отложить от точки О так, чтобы момент пары сил (F1, F`1) совпадал с главным моментом MOz (рис. 5.4, б). В результате приведения системы сил к данному центру могут встретиться следующие случаи: (1) Fo≠0, MOz≠0.В этом случае система сил может быть приведена к одной силе (равнодействующей), как это показано на рис. 5.4, в.(2) Fo≠0, МОz=0. В этом случае система сил приводится к одной силе (равнодействующей),  проходящей через данный центр  приведения. (3) Fo=0, MOz≠0. При этом система сил эквивалентна  одной  паре сил. (4) Fo=0, МОz=0. В этом случае рассматриваемая система сил эквивалентна нулю, т.  е.  силы,  составляющие систему,  взаимно уравновешены.

Теорема Вариньона

Теорема Вариньона. Если рассматриваемая плоская система сил приводится к равнодействующей, то момент этой равнодействующей относительно какой-либо точки равен алгебраической сумме моментов всех сил данной системы относительно той оке самой точки. Предположим, что система сил приводится к равнодействующей R, проходящей через точку О. Возьмем теперь в качестве центра приведения другую точку O₁. Главный момент (5.5) относительно этой точки равен сумме моментов всех сил: M_O1Z=åM_o1z(F_k)   (5.11). С другой стороны, имеем M_O1Z=M_Olz(R), (5.12) так как главный момент для центра приведения О равен нулю (M_Oz=0). 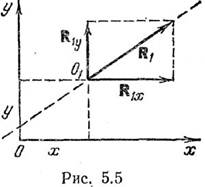Сравнивая соотношения (5.11) и (5.12), получаем M_O1z(R)=åM_OlZ(F_k); (5.13) ч.т.д. При помощи теоремы Вариньона можно найти уравнение линии действия равнодействующей. Пусть равнодействующая R₁ приложена в какой-либо точке О₁ с координатами х и у (рис. 5.5) и известны главный вектор F_o и главный момент М_Оя  при центре приведения в начале координат. Так как R₁=F_o, то составляющие равнодействующей по осям х и у равны R_lx=F_Ox=F_Oxi и R_ly=F_Oy=F_oyj. Согласно теореме Вариньона момент равнодействующей относительно начала координат равен главному моменту при центре приведения в начале координат, т. е. М_оz=M_Oz(R₁)=xF_Oy–yF_Ox. (5.14). Величины M_Oz, F_Ox и F_oy при переносе точки приложения равнодействующей вдоль ее линии действия не изменяются, следовательно, на координаты х и у в уравнении (5.14) можно смотреть как на текущие координаты линии действия равнодействующей. Таким образом, уравнение (5.14) есть уравнение линии действия равнодействующей. При F_ox≠0 его можно переписать в виде y=(F_oy/F_ox)x–(M_oz/F_ox).

Условия равновесия плоской системы сил

Необходимым и достаточным условием равновесия системы сил является равенство нулю главного вектора и главного момента. Для плоской системы сил эти условия получают вид F_o=åF_k=0, М_Оz=åМ_oz(F_k)=0, (5.15), где О– произвольная точка в плоскости действия сил. Получим: F_ox=åF_kx=F_1x+F_2x+…+F_nx=0, P_ox=åF_ky=F_1y+F_2y+…+F_ny=0, М_Оz=åM_Oz(F_k)=M_oz(F₁)+M_oz(F₂)+…+M_oz(F_n)=0, т. е. для равновесия плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на две координатные оси и алгебраическая сумма моментов всех сил относительно произвольной точки равнялись нулю. Второй  формой уравнения равновесия является равенство нулю алгебраических сумм моментов всех сил относительно любых трех точек, не лежащих на одной прямой; åM_Az(F_k)=0, åM_Bz(F_k)=0, åM_Cz(F_k)=0, (5.17), где A, В и С– указанные точки. Необходимость выполнения этих равенств вытекает из условий (5.15). Докажем их достаточность. Предположим, что все равенства (5.17) выполняются. Равенство нулю главного момента при центре приведения в точке А возможно, либо если система приводится к равнодействующей (R≠0) и линия ее действия проходит через точку А, либо R=0; аналогично равенство нулю главного момента относительно точек В и С означает, что либо R≠0 и равнодействующая проходит через обе точки, либо R=0. Но равнодействующая не может проходить через все эти три точки А, В и С (по условию они не лежат на одной прямой). Следовательно, равенства (5.17) возможны лишь при R=0, т. е. система сил находится в равновесии. Заметим, что если точки А, В и С лежат на одной прямой, то выполнение условий (5.17) не будет достаточным условием равновесия, — в этом случае система может быть приведена к равнодействующей, линия действия которой проходит через эти точки.

Третья форма уравнений равновесия плоской системы сил

Третьей формой уравнений равновесия плоской системы сил является равенство нулю алгебраических сумм моментов всех сил системы относительно двух любых точек и равенство нулю алгебраической суммы проекций всех сил системы на ось, не перпендикулярную прямой, проходящей  через две выбранные  точки; åМ_Аz(F_k)=0, åМ_Bz(F_k)=0, åF_kx=0 (5.18) (ось х не перпендикулярна отрезку А В).Необходимость выполнения этих равенств для равновесия сил вытекает непосредственно из условий (5.15). 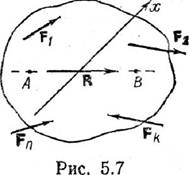Убедимся в том, что выполнения  этих  условий  достаточно для  равновесий  сил. Из первых двух равенств, как и в предыдущем случае, вытекает, что если система сил имеет равнодействующую, то ее линия действия проходит через точки А и В (рис. 5.7). Тогда проекция равнодействующей на ось х, не перпендикулярную отрезку АВ, окажется отличной от нуля. Но эта возможность исключается третьим уравнением (5.18) так как R_x=åF_hx). Следовательно, равнодействующая должна равняться нулю и система находится в равновесии. Если ось х будет перпендикулярна отрезку АВ, то уравнения (5.18) не будут достаточными условиями равновесия, так как в этом случае система может иметь равнодействующую, линия действия  которой  проходит через точки А и В. Т.о., система уравнений равновесия может содержать одно уравнение моментов и два уравнения проекций, либо два уравнения моментов и одно уравнение проекций, либо три уравнения моментов. Пусть линии действия всех сил параллельны оси у (рис. 4.8). Тогда уравнения равновесия для рассматриваемой системы параллельных сил будут åF_ky=0, åM_Oz(F_k)=0.(5.19). åM_Az(F_k)=0, åM_Bz(F_k)=0, (5.20) причем точки А и B не должны лежать на прямой, параллельной оси у. Система сил, действующих на твердое тело, может состоять как из сосредоточенных (изолированных) сил, так и распределенных сил. Различают силы, распределенные по линии, по поверхности и по объему тела.

Равновесие тела при наличии трения скольжения

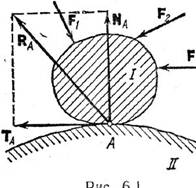
Если два тела I и II (рис. 6.1) взаимодействуют друг с другом, соприкасаясь в точке А, то всегда реакцию R_A, действующую, например, со стороны тела II и приложенную к телу I, можно разложить на две составляющие: N_A, направленную по общей нормали к поверхности соприкасающихся тел в точке А, и Т_А, лежащую в касательной плоскости. Составляющая N_A называется нормальной реакцией, сила Т_А называется силой трения скольжения — она препятствует скольжению тела I по телу II. В соответствии с аксиомой 4 (третьим законом Ньютона) на тело II со стороны тела I действует равная по модулю и противоположно направленная сила реакции. Ее составляющая, перпендикулярная касательной плоскости, называется силой нормального давления. Сила трения Т_А = 0, если соприкасающиеся поверхности идеально гладкие. В реальных условиях поверхности шероховаты и во многих случаях пренебречь силой трения нельзя. Максимальная   сила   трения   приближенно пропорциональна нормальному давлению, т. е. T_max=fN. (6.3)– закон Амонтона—Кулона. Коэффициент f называется коэффициентом трения скольжения. Его значение  не зависит от площади соприкасающихся поверхностей, но зависит от материала и степени шероховатости соприкасающихся поверхностей. Силу трения можно вычислить по ф-ле T=fN только если имеет место критический случай. 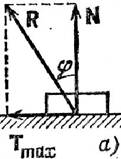В других случаях силу трения следует определять из ур-ий равнов. На рисунке показана реакция R (здесь активные силы стремятся сдвинуть тело вправо). Угол j между предельной реакцией  R и нормалью к поверхности называется  углом   трения. tgj=T_max/N=f.

Геометрическое место всех возможных направлений предельной реакции R образует коническую поверхность — конус трения (рис. 6.6, б). Если коэффициент трения f во всех направлениях одинаков, то конус трения будет круговым. В тех случаях, когда коэффициент трения f зависит от направления возможного движения тела, конус трения  не будет  круговым. Если равнодействующая активных сил. 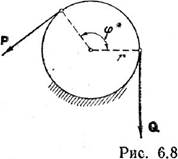находится внутри конуса трения, то увеличением ее модуля нельзя нарушить равновесие тела; для того чтобы тело начало движение, необходимо (и достаточно), чтобы равнодействующая активных сил F находилась вне конуса трения. Рассмотрим трение гибких тел (рис.6.8). Формула Эйлера помогает найти наименьшую силу P, способную уравновесить силу Q. P=Qe^-fj*. Можно так же найти такую силу P, способную преодолеть сопротивление трения вместе с силой Q. В этом случае в формуле Эйлера поменяется только знак f: P=Qe^fj*.

Равновесие тела при наличии трения качения

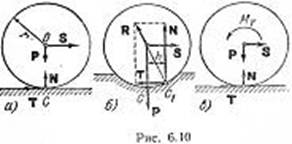
Рассмотрим цилиндр (каток), покоящийся на горизонтальной плоскости, когда на него действует горизонтальная активная сила S; кроме нее, действуют сила тяжести Р, а также нормальная реакция N и сила трения Т (рис. 6.10, а). При достаточно малом модуле силы S цилиндр остается в покое. Но этот факт нельзя объяснить, если удовлетвориться введением сил, изображенных на рис. 6.10, а. Согласно этой схеме равновесие невозможно, так как главный момент всех сил, действующих на цилиндр М_Сz= –Sr, отличен от нуля, и одно из условий равновесия не выполняется. Причина этого несоответствия состоит в том, что мы представляем это тело абсолютно твердым и предполагаем касание цилиндра с поверхностью происходящим по образующей. Для устранения отмеченного несоответствия теории с опытом необходимо отказаться от гипотезы абсолютно твердого тела и учесть, что в действительности цилиндр и плоскость вблизи точки С деформируются и существует некоторая площадь соприкосновения конечной ширины. Вследствие этого в ее правой части цилиндр прижимается сильнее, чем в левой, и полная реакция R приложена правее точки С (см. точку С₁ на рис. 6.10, б). Полученная схема действующих сил статически удовлетворительна, так как момент пары (S,Т) может уравновеситься моментом пары (N,Р). В отличие от первой схемы (рис. 6.10, а), к цилиндру приложена пара сил с моментом М_T=Nh.(6.11). Этот  момент называется  моментом  трения качения. h=Sr/, где h-расстояние от C до C₁. (6.13). С увеличением модуля активной силы S растет расстояние h. Но это расстояние связано с площадью поверхности контакта и, следовательно, не может неограниченно увеличиваться. Это значит, что наступит такое состояние, когда увеличение силы S приведет к нарушению равновесия. Обозначим максимально возможную величину h буквой d. Величина d пропорциональна радиусу цилиндра и различна для разных материалов. Следовательно, если имеет место равновесие, то выполняется условие: h<=d.(6.14). d называется коэффициентом трения качения; она имеет размерность длины. Условие (6.14) можно также записать в виде М_т<=dN, или, учитывая (6.12), S<=(d/r)N.(6.15).  Очевидно, что максимальный момент трения качения M_T^max=dN  пропорционален  силе  нормального давления.

Центр параллельных сил

Условия приведения системы параллельных сил к равнодействующей сводятся к одному неравенству F≠0. Что же происходит с равнодействующей R при одновременном повороте линий действия данных параллельных сил на один и тот же угол, если точки приложения этих сил сохраняются неизменными и повороты линий действия сил происходят вокруг параллельных осей. При этих условиях равнодействующая заданной системы сил также одновременно поворачивается на тот же угол, причем поворот происходит вокруг некоторой фиксированной точки, которая называется центром параллельных сил. Перейдем к доказательству этого утверждения. 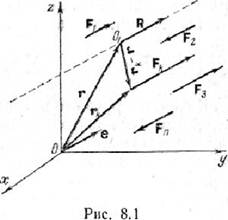Предположим, что для рассматриваемой системы параллельных сил F₁, F₂,...,F_n главный вектор не равен нулю, следовательно, данная система сил приводится к равнодействующей. Пусть точка О₁ есть какая-либо точка линии действия этой равнодействующей. Пусть теперь r– радиус-вектор точки 0₁ относительно выбранного полюса O, a r_k — радиус-вектор точки приложения силы F_k (рис. 8.1). Согласно теореме Вариньона сумма моментов всех сил системы относительно точки 0₁ равна нулю: å(r_k–r)xF_k=0, т.е. år_kxF_k–årxF_k=år_kxF_k–råF_k=0. Введём единичный вектор e, тогда любая сила F_k может быть представлена в виде F_k=F^*_ke (где F^*_k=F_h, если направление силы F_h и вектора е совпадают, и F^*_k=–F_h, если F_k и е направлены противоположно друг другу); åF_k=eåF^*_k. Получим: år_kxF^*_ke–rxeåF^*_k=0, откуда [år_kF^*_k–råF^*_k]xe=0. Последнее равенство удовлетворяется при любом направлении сил (т. е. направлении единичного вектора е) только при условии, что первый множитель равен нулю: år_kF^*_k–råF^*_k=0. Это рав-во имеет единственное решение относительно радиуса-вектора r, определяющего такую точку приложения равнодействующей, которая не меняет своего положения при повороте линий действия сил. Такой точкой и является центр параллельных сил. Обозначив радиус-вектор центра параллельных сил через г_с: r_c=(år_kF^*_k)/(åF^*_k)=(r₁F^*₁+r₂F^*₂+…+r_nF^*_n)/ (F^*₁+F^*₂+…+F^*_n). Пусть х_с, у_с, z_с– координаты центра параллельных сил, a x_k, y_k, z_k– координаты точки приложения произвольной силы F_k; тогда координаты центра параллельных сил найдутся из формул:

x_c=(x_kF^*_k)/(F^*_k)=(x₁F^*₁+x₂F^*₂+…+x_nF^*_n)/ (F^*₁+F^*₂+…+F^*_n), y_c=(y_kF^*_k)/(F^*_k)=

=(y₁F^*₁+y₂F^*₂+…+y_nF^*_n)/ (F^*₁+F^*₂+…+F^*_n), z_c=

=(z_kF^*_k)/(åF^*_k)=(z₁F^*₁+z₂F^*₂+…+z_nF^*_n)/ (F^*₁+F^*₂+…+F^*_n)

Выражения x_kF^*_k, y_kF^*_k, z_kF^*_k называются статическими моментами заданной  системы  сил соответственно относительно координатных плоскостей yOz, xOz, xOy. Если начало координат выбрано в центре параллельных сил, то х_с=у_с=z_с=0, и статические моменты заданной системы сил равны нулю.

Центр тяжести

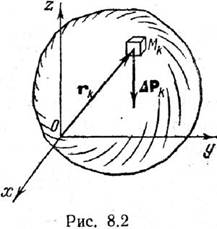
Тело произвольной формы, находящееся в поле сил тяжести, можно разбить сечениями, параллельными координатным плоскостям, на элементарные объемы (рис. 8.2). Если пренебречь размерами тела по сравнению с радиусом Земли, то силы тяжести, действующие на каждый элементарный объем, можно считать параллельными друг другу. Обозначим через DV_k объем элементарного параллелепипеда с центром в точке M_k (см. рис. 8.2), а силу тяжести, действующую на этот элемент, – через DP_k. Тогда средним удельным весом элемента объема называется отношение DP_k/DV_k. Стягивая параллелепипед в точку М_k, получим удельный вес в данной точке тела, как предел среднего удельного веса g(x_k, y_k, z_k)=lim_DVk®0[DP_k/DV_k] (8.10).  Таким образом, удельный вес является функцией координат, т.е. g=g(x, y, z). Будем считать, что вместе с геометрическими характеристиками тела задан также и удельный вес в каждой точке тела. Вернемся к разбиению тела на элементарные объемы. Если исключить объемы тех элементов, которые граничат с поверхностью тела, то можно получить ступенчатое тело, состоящее из совокупности параллелепипедов. Приложим к центру каждого параллелепипеда силу тяжести DP_k=g_kDV_k, где g_h — удельный вес в точке тела, совпадающей с центром параллелепипеда. Для системы п параллельных сил тяжести, образованной таким образом, можно найти центр параллельных сил r⁽ⁿ⁾=(år_kDP_k)/(åDP_k)= (r₁DP₁+r₂DP₂+…+r_nDP_n)/ (DP₁+DP₂+…+DP_n). Эта формула определяет положение некоторой точки С_n. Центром тяжести называется точка,  являющаяся предельной для точек С_n при п®µ.