Динамические матрицы

Переводим с английского

Другие статьи автора

---

Win-word.zip

ГАРМОНИЧЕСКИЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Косинов Н.В.

E-mail: kosinov@unitron.com.ua

Аннотация

Показана принадлежность последовательностей Фибоначчи и Люка к обобщенным классам числовых последовательностей и связь числовых инвариантов обобщенных последовательностей с золотой пропорцией. Числа Фибоначчи и Люка являются примерами гармонических последовательностей. Константой последовательностей Фибоначчи и Люка или их числовым инвариантом является золотая пропорция (Ф=1,618033). Эти последовательности являются частными случаями обобщенной алгебраической последовательности, имеющей рекуррентное свойство вида: a(n)=ka(n-1)+a(n-2) при k =1. Если k >1, то константами последовательностей являются числа, имеющие свойства, близкие к свойствам золотой пропорции. Уравнения X±1/X= k позволяют получить для последовательностей, имеющих рекуррентное соотношение a(n) = ka(n-1) ± a(n-2), большое семейство числовых инвариантов, близких по свойствам к золотой пропорции. Приведен пример последовательности, имеющей фрактальную триадную структуру.

1. Введение

Числовые последовательности Фибоначчи и Люка являются примерами гармонических последовательностей. Константой последовательностей Фибоначчи и Люка или их числовым инвариантом является золотая пропорция (Ф=1,618033). Интерес к золотой пропорции и числам Фибоначчи и Люка порожден не только тем, что с ними связаны целые области в культуре и науке, но в большей степени тем, что они очень часто встречаются во многих явлениях окружающего мира. Поэтому важно выяснить к каким обобщенным классам последовательностей относятся числа Фибоначчи и Люка, и как связаны числовые инварианты других последовательностей с золотой пропорцией.

2. Гармонические последовательности с рекуррентным свойством: a(n)=ka(n-1)+a(n-2)

Рассмотрим последовательности вида:

.

При k=1 получим рекуррентную формулу:

.

Эта рекуррентная формула при a(0) = 1, a(1)=1 порождает числа Фибоначчи: Ф(n) = 1, 1, 2, 3, 5, 8, 13… При a(0) =2 и при a(1)=1 формула порождает числа Люка: L(n)= 2, 1, 3, 4, 7, 11…

Для этих последовательностей отношение соседних членов стремится в пределе к золотой пропорции:

Число Ф является числовым инвариантом или константой этих последовательностей. Число Ф единственное положительное число, которое переходит в обратное ему при вычитании единицы. Обратная величина числа Ф в точности равна числу, стоящему после запятой. Константа этого семейства последовательностей является корнем уравнения вида: X₁–1/X₁=1.

При k=2 получим рекуррентную формулу:

Эта рекуррентная формула при a(0) = 2 и при a(1)=2 порождает главную последовательность вида: K₂(n) = 2, 2, 6, 14, 34, 82, 198… В энциклопедии Нейла Слоуна эта последовательность зарегистрирована под номером A002203 [1].

Для последовательностей этого класса:

Число X₂ является числовым инвариантом или константой этого семейства последовательностей. Число X₂ обладает особенным свойством - оно переходит в обратное ему при вычитании целой части. Обратная величина числа X₂ в точности равна числу, стоящему после запятой. В этом число X₂ проявляет сходство с золотой пропорцией. Константа этого семейства последовательностей является корнем уравнения вида: X₂–1/X₂=2. У всякой последовательности с рекуррентным свойством a(n) = 2a(n-1) + a(n-2) с любыми начальными членами отношение соседних членов по мере удаления от начала стремится к X₂=2,41421356…

При k=3 получим рекуррентную формулу:

Эта рекуррентная формула при a(0) = 2 и при a(1)=3 порождает главную последовательность вида: K₃(n) = 2, 3, 11, 36, 119, 393, 1298… В энциклопедии Нейла Слоуна эта последовательность зарегистрирована под номером A006497 [1].

Для последовательностей этого класса:

Число X₃ является числовым инвариантом или константой этих последовательностей. Число X₃ переходит в обратное ему при вычитании целой части. Обратная величина числа X₃ в точности равна числу, стоящему после запятой. Константа этого семейства последовательностей является корнем уравнения вида: X₃–1/X₃=3.

При k=8 получим рекуррентную формулу:

Эта рекуррентная формула при a(0) = 2 и при a(1)=8 порождает главную последовательность вида: K₈(n) = 2, 8, 66… В энциклопедии Нейла Слоуна эта последовательность зарегистрирована под номером A086594 [1].

Для последовательностей этого класса:

Число X₈ является числовым инвариантом или константой этих последовательностей. Число X₈ переходит в обратное ему при вычитании целой части. Обратная величина числа X₈ в точности равна числу, стоящему после запятой. Константа этого семейства последовательностей является корнем уравнения вида: X₈–1/X₈=8.

Уравнения X–1/X= k позволяют получить для последовательностей, имеющих рекуррентное соотношение a(n) = ka(n-1) + a(n-2), большое семейство числовых инвариантов, близких по свойствам к золотой пропорции. Примерами чисел со свойствами, близкими к свойствам золотой пропорции, являются: X₂ = 2,414213562…, X₃ = 3,302775637…, X₄ = 4,23606…, X₅ = 5,192582403…, X₁₁ = 11,0901… Их обратные значения дают числа, стоящие после запятой: 1/X₂ = 0,414213562…, 1/X₃ = 0,302775637…, 1/X₄ = 0,23606…, 1/X₅ = 0,192582403…, 1/X₁₁ = 0,0901…

Для произвольного k из формулы a(n)=ka(n-1)+a(n-2) при a(0) = 2 и при a(1)= k получим алгебраическую последовательность вида: 2, k, k^2+2, k^3+3k, k^4+4k^2+2, k^5+5k^3+5k, k^6+6k^4+9k^2+2, k^7+7k^5+14k^3 +7k, k^8+8k^6+20k^4+16k^2+2, k^9+9k^7+27k^5 +30k^3+9k, k^10+10k^8+35k^6+50k^4+25k^2+2…

Для этой алгебраической последовательности:

Числа X_k являются числовыми инвариантами или константами алгебраической последовательности. Четные и нечетные члены алгебраической последовательности вычисляются по формулам Бине:

Любые произвольные члены алгебраической последовательности вычисляются по следующей формуле:

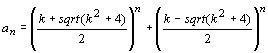
Формула: a(n) =((k+sqrt(k^2+4))/2)^n + ((k-sqrt(k^2+4))/2)^n дает большой класс главных последовательностей, первые члены которых равны 2, k . Действительно, нулевой член обобщенной последовательности: a(0) =((k+sqrt(k^2+4))/2)^0 + ((k-sqrt(k^2+4))/2)^0 = 2.

Первый член обобщенной последовательности: a(1) =((k+sqrt(k^2+4))/2)^1 + ((k-sqrt(k^2+4))/2)^1 = 2k/2=k, и т.д.

Для этих последовательностей справедливы следующие формулы:

,

.

Одна алгебраическая последовательность порождает большое количество частных числовых последовательностей и дает возможность легко найти новые последовательности данного класса. При конкретном значении k обобщенная алгебраическая последовательность позволяет получить одну из частных последовательностей.

3. Гармонические последовательности с рекуррентным свойством: a(n)=ka(n-1) - a(n-2)

Рассмотрим последовательности вида:

При k=1 получим рекуррентную формулу:

Для определения первых членов главной последовательности этого семейства рассмотрим уравнение: X₁+1/X₁=1. Отметим, что это уравнение не имеет действительных корней. Первый корень уравнения: X_1,1 = (1+sqrt(–3))/2. Второй корень уравнения:X_1,2 = (1–sqrt(–3))/2. Нулевой член последовательности: a(0)= ((1+sqrt(–3))/2)⁰ + ((1–sqrt(–3))/2)⁰ =2. Первый член последовательности: a(1)= (1+sqrt(–3))/2 + (1–sqrt(–3))/2=1. Второй член последовательности: a(2)= ((1+sqrt(–3))/2)² + ((1–sqrt(–3))/2)² =-1.

Рекуррентная формула a(n)=a(n-1) - a(n-2) при a(0) = 2 и при a(1)=1 порождает числа:

S₁(n) = 2, 1, -1, -2, -1, 1, 2, 1, -1, -2, -1, 1, 2, 1, …

Это особенная числовая последовательность. Особенность ее состоит в том, что она имеет триадную структуру. Для этой последовательности числовыми инвариантами являются сами члены последовательности. Эта последовательность обладает уникальным свойством – она является фрактальной. Рекуррентная формула a(n) = a(n-1) – a(n-2), порождающая фрактальную последовательность, является симметричной математической конструкцией по отношению к рекуррентной формуле a(n) = a(n-1) + a(n-2), порождающей числа Люка. Уравнение для определения числового инварианта фрактальной последовательности также симметрично аналогичному уравнению для последовательности Люка.

При k=2 получим рекуррентную формулу:

Эта рекуррентная формула при a(0) = 2 и при a(1)=2 порождает главную последовательность вида:

S₂(n) = 2, 2, 2, 2, 2, 2, 2,… В энциклопедии Нейла Слоуна эта последовательность зарегистрирована под номером A007395 [1].

Для последовательностей этого класса:

Число X₂ является числовым инвариантом или константой этих последовательностей. Число X₂ обладает особенным свойством, оно переходит в ближайшее целое число при добавлении к нему обратного числа. Константа этого семейства последовательностей является корнем уравнения вида: X₂+1/X₂=2.

При k=3 получим рекуррентную формулу:

Эта рекуррентная формула при a(0) = 2 и при a(1)=3 порождает главную последовательность вида: K_3-(n) = 2, 3, 7, 18, 47, 123, 322… В энциклопедии Нейла Слоуна эта последовательность зарегистрирована под номером A005248 [1].

Для последовательностей этого класса:

Число X₃ является числовым инвариантом или константой этого семейства последовательностей. Число X₃ переходит в ближайшее целое число при добавлении к нему обратного числа. Константа этого семейства последовательностей является корнем уравнения вида: X₃+1/X₃=3.

При k=8 получим рекуррентную формулу:

Эта рекуррентная формула при a(0) = 2 и при a(1)=8 порождает главную последовательность вида: K_8-(n) = 2, 8, 62, 488… В энциклопедии Нейла Слоуна эта последовательность зарегистрирована под номером A086903 [1].

Для последовательностей этого класса:

Число X₈ является числовым инвариантом или константой этого семейства последовательностей. Число X₈ переходит в ближайшее целое число при добавлении к нему обратного числа. Константа этого семейства последовательностей является корнем уравнения вида: X₈+1/X₈=8.

Уравнения X+1/X=k позволяют получить для последовательностей, имеющих рекуррентное соотношение a(n) = ka(n-1) – a(n-2), большое семейство числовых инвариантов, с указанными выше свойствами. Примерами чисел с такими свойствами являются: X₂ = 1,00000…, X₃ = 2,61803…, X₄ = 3,73205…, X₅ = 4,79128…, X₁₁ = 10,9083… Их обратные значения являются дополнениями этих чисел до ближайшего целого числа: 1/ X₂ = 1,000000…, 1/ X₃ = 0,3819…, 1/ X₄ = 0,26794…, 1/X₅ = 0,20871…, 1/ X₁₁ = 0,0916…

Для произвольного k из формулы a(n)=ka(n-1) – a(n-2) при a(0) = 2 и при a(1)= k получим обобщенную алгебраическую последовательность вида: 2, k, k^2-2, k^3-3k, k^4-4k^2+2, k^5-5k^3+5k, k^6-6k^4+9k^2-2,k^7-7k^5+14k^3-7k, k^8-8k^6+20k^4-16k^2+2, k^9-9k^7+27k^5-30k^3+9k, k^10-10k^8+35k^6-50k^4+25k^2-2…

Для этой алгебраической последовательности:

Числа X_k- являются числовыми инвариантами или константами обобщенной алгебраической последовательности. Члены алгебраической последовательности вычисляются по следующим формулам:

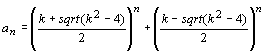
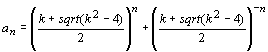
Формула: a(n) =((k+sqrt(k^2-4))/2)^n + ((k-sqrt(k^2-4))/2)^n дает класс главных последовательностей. Нулевой член алгебраической последовательности: a(0) =((k+sqrt(k^2-4))/2)^0 + ((k-sqrt(k^2-4))/2)^0 = 2. Первый член алгебраической последовательности: a(1)=((k+sqrt(k^2-4))/2)^1 + ((k-sqrt(k^2-4))/2)^1 = 2k/2=k. Второй член алгебраической последовательности: a(2) =((k+sqrt(k^2-4))/2)^2 + ((k-sqrt(k^2-4))/2)^2 = k^2-2 и т.д.

Для этих последовательностей справедлива следующая формула:

.

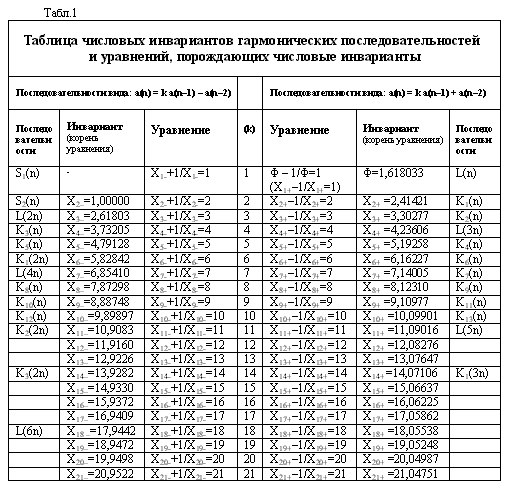
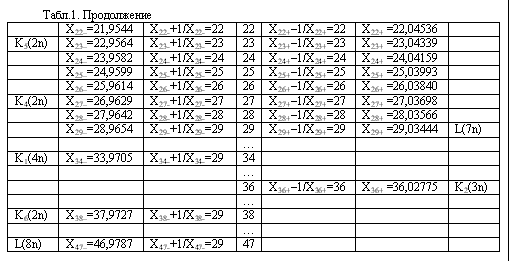
Одна обобщенная алгебраическая последовательность порождает большое количество частных последовательностей и дает возможность легко найти новые последовательности данного класса. В таблице 1 приведены числовые инварианты гармонических последовательностей и уравнения, порождающие числовые инварианты.

4. Выводы

Таким образом, золотая пропорция (Ф=1,618033), выполняя роль числового инварианта последовательностей Фибоначчи и Люка, является частным решением обобщенного уравнения X–1/X=k при k =1. Соответственно, последовательности чисел Фибоначчи и Люка являются частными случаями обобщенных алгебраических последовательностей, определяемых обобщенным рекуррентным соотношением a(n)=ka(n-1) ± a(n-2) при k=1. Для обобщенных последовательностей числовыми инвариантами являются константы, которые близки по своим свойствам к свойствам золотой пропорции. Числовые инварианты гармонических последовательностей группируются в семейства, члены которых представлены степенными функциями главных инвариантов. Среди констант гармонических последовательностей есть целое семейство числовых инвариантов, которые являются степенными функциями золотой пропорции. Рекуррентная формула a(n)=a(n-1)–a(n-2) при a(0)=2, a(1)=1 симметричная формуле a(n)=a(n-1)+a(n-2), порождающей числа Люка, дает последовательность вида: S₁(n) = 2, 1, -1, -2, -1, 1, 2, 1, -1, -2, -1, 1, 2, 1, …, которая, по всей видимости, имеет фундаментальный статус и должна проявляться в природных явлениях.

Источники информации

1. Neil J.A.Sloane http://www.research.att.com/~njas/sequences/