Динамические матрицы

Переводим с английского

Другие статьи автора

---

Win-word.zip

ФИЗИЧЕСКИЙ ЭКВИВАЛЕНТ ЧИСЛА "Пи" И ГЕОМЕТРИЧЕСКИЙ ЭКВИВАЛЕНТ ПОСТОЯННОЙ ТОНКОЙ СТРУКТУРЫ "альфа".

Косинов.Н.В

E-mail: kosinov@unitron.com.ua

Аннотация

Число π совместно с постоянной тонкой структуры α позволяют получить важные безразмерные фундаментальные константы, которые иным способом получить не удавалось. Показано, что константы π и α являются константами одного класса. В рамках этого класса констант найден физический эквивалент числа π, в качестве которого выступает число α₂ =7,49648184638205•10^-3 или его обратное значение α₂^-1 =133,395907639344. Этой новой константе определен статус второй постоянной тонкой структуры. Геометрическим эквивалентом постоянной тонкой структуры α является число π₂= 1,83360822(13), которое совместно с π = 3,14159265358979… дает возможность получить простые числовые множители перед большими числами Дирака.

1. Проблема постоянной тонкой структуры

Постоянная тонкой структуры была введена в физику Зоммерфельдом в 1916 году при создании теории тонкой структуры энергии атома. Первоначально постоянная тонкой структуры (α) была определена как отношение скорости электрона на низшей боровской орбите к скорости света. С развитием квантовой теории стало понятно, что такое упрощенное представление не объясняет ее истинный смысл. До сих пор природа происхождения этой константы не раскрыта. Кроме тонкой структуры энергии атома эта константа проявляется в следующей комбинации фундаментальных физических констант: α = μ₀ce²/2h. По поводу того, что константа (α) появляется в соотношении, связывающем постоянную Планка, заряд и скорость света Дирак писал [1]: "неизвестно почему это выражение имеет именно такое, а не иное значение. Физики выдвигали по этому поводу различные идеи, однако общепринятого объяснения до сих пор нет". Аналогичное высказывание о числе (α) принадлежит Фейнману [2]: "с тех пор как оно было открыто... оно было загадкой. Всех искушенных физиков-теоретиков это число ставило в тупик и тем самым вызывало беспокойство. Непосредственно вам хотелось бы знать, откуда эта постоянная связи появилась: связана ли она с числом π или может быть она связана с натуральными логарифмами? Никто не знает". Относительно значения постоянной тонкой структуры авторы Берклеевского курса физики пишут [3]: "мы не располагаем теорией, которая предсказывала бы величину этой постоянной".

Проблема постоянной тонкой структуры является одной из 10 важнейших проблем физики, которые названы “проблемами тысячелетия” [4,5]. В числе этих проблем она сформулирована так: “являются ли все безразмерные параметры, которые характеризуют Вселенную вычисляемыми в принципе или они являются следствием квантово-механической случайности и невычисляемы?”.

По-прежнему остается открытым вопрос: существует ли связь у этой константы с важнейшими геометрическими константами, например с числом π ? Число π, известное еще античным математикам, принадлежит к фундаментальным математическим константам и обладает уникальными особенностями. Несмотря на то, что π является математическим числом, оно входит во многие формулы физики. Это созвучно с утверждениями ученых о связи физики и геометрии. Здесь уместно сослаться на мнение А.Пуанкаре о дополнительности физики и геометрии. Согласно Пуанкаре, на опыте мы всегда наблюдаем некую “сумму” физики и геометрии [10]. Подобная “сумма” физики и геометрии проявляется на примере первичного, онтологического базиса фундаментальных констант (табл.1) в виде самостоятельных групп физических и геометрических констант [7]. В этом пятиконстантном онтологическом базисе – три суперконстанты размерные, а две – безразмерные. Пяти первичных суперконстант достаточно, чтобы на их основе получить расчетным путем множество других констант [6,7,9].

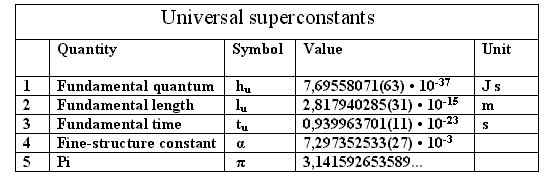Табл.1.

Кроме постоянной тонкой структуры α в физике существуют и другие безразмерные константы. К числу важных безразмерных констант относятся большие числа порядка 10³⁹ –10⁴⁴, которые часто встречаются в физических уравнениях. Считая совпадения больших чисел не случайными, П.Дирак сформулировал следующую гипотезу больших чисел [15]: ”В качестве общего принципа можно принять, что все большие числа порядка 10³⁹, 10⁷⁸ и т.д., встречающиеся в общей физической теории, с точностью до простых числовых множителей равны t, t² и т.д., где t - время в современную эпоху, выраженное в атомных единицах. Упомянутые простые числовые множители должны определяться теоретически, когда будет создана полная теория космологии и атомизма.” В теоретической физике так и осталась эта таинственная проблема совпадения больших чисел не решенной. Не удалось создать “полную теорию космологии и атомизма”, на что надеялся П.Дирак [15]. Не удалось вывести большие числа математически, как это хотел П.Девис [16]. Не дошло дело и до выяснения истинных значений, упомянутых П.Дираком, “простых числовых множителей” перед большими числами.

2. Вторая постоянная тонкой структуры α₂.

В [6,11] сформулирован принцип, согласно которому все безразмерные константы происходят от чисел π и α. Например, комбинация этих констант дает большое число D_o [11]:

. Исходя из симметрии формулы, обозначим. Отсюда получим: Обратная ей величина имеет следующее значение: α₂^-1 = 133,395907639344... Новая константа α₂ является физическим эквивалентом числа π. Эта константа появляется в соотношениях совместно с постоянной тонкой структуры α. Назовем эту физическую постоянную второй константой тонкой структуры (Fine-structure constant – 2). С использованием новой физической константы α₂ онтологический базис фундаментальных физических констант примет вид (табл.2):

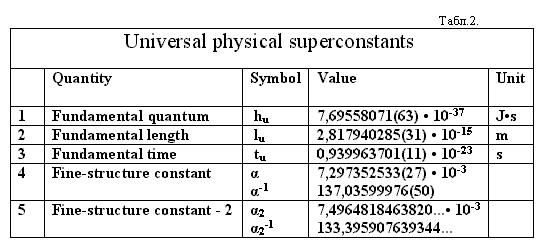
3. Число π₂ - геометрическая характеристика искривленного пространства.

Используя постоянную тонкой структуры α, получим новую константу, которая является ее геометрическим эквивалентом: . Число π₂ – это геометрическая характеристика искривленного пространства [8]. Это число аналогично числу π - геометрической характеристикой плоского евклидова пространства. Значения эквивалентов констант π и α приведены в таблице 3.

Очевидно, для π₂ существуют сходящиеся ряды аналогичные рядам, приводящим к числу π. Необходимо вести поиск таких рядов. Нахождение таких рядов позволило бы получить точное значение π₂, сравнимое с точностью числа π.

Соотношения для чисел π и α и для их физического и геометрического эквивалентов α₂ и π₂ полностью симметричны:

, , , .

Константы π и α₂ характеризуют плоское псевдоевклидово пространство. При этом, π является геометрической характеристикой плоского пространства, а α₂ его физической характеристикой. Константы π₂ и α характеризуют искривленное пространство. При этом, π₂ является геометрической характеристикой искривленного пространства, а α его физической характеристикой. Для этих четырех констант справедливо следующее соотношение:

4. Новые возможности для физической теории.

Две новые константы α₂ и π₂ совместно с числами α и π открывают новые возможности для физической теории. Так, например, отношение α/α₂ дает константу структурогенеза [13]: k_s=0,9734369645(30). Она позволяет получить теоретическим расчетом константу m_p/m_e, значение которой до настоящего времени теоретического обоснования не имело. Формула для вычисления значения m_p/m_e следует из фрактала протона [14]:

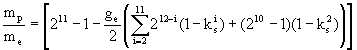
Константа структурогенеза k_s задает значение дефекта масс для частиц, участвующих в структурогенезе вещества [13]. Произведение (π π₂)^-1/2 дает значение простого множителя перед большим числом, на необходимость поиска которого указывал П.Дирак [15]: . Произведение α^-1 на α₂^-1 в десятой степени дает большое число D₀ [15]: . Комбинация констант π, α, π₂, α₂ в виде произведений (π α₂^-20) и (π₂ α^-20) дает значение большого числа D_u (табл.4):

,

.

Произведения четырех констант π, α₂^-20, π₂, α^-20 дают большое число D_u²:

.

Константы π и π₂ совместно с константами m_p , m_e, D_u, позволяют получить с большой точностью значение большого числа D, на которое впервые обратил внимание П.Дирак [15]: .

Таким образом, удалось получить большое космологическое число, на чем акцентировал внимание П.Девис [16], включая и “простые числовые множители”, на что указывал П.Дирак [15].

В таблице 4 приведены формулы для вычисления значений больших чисел и их значения.

5. Семейство констант, происходящих от чисел π, α, π₂, α₂.

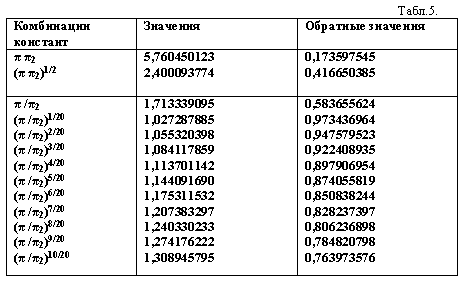
Ниже приведены значения комбинаций констант, которые встречаются в формулах структурогенеза вещества, в формулах больших чисел, а также в коэффициентах перед большими числами. Значения констант, порожденных числами π и π₂, приведены в таблице 5.

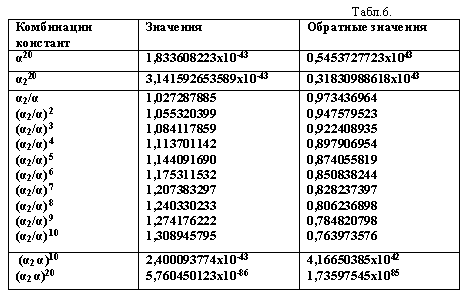
Значения констант, порожденных числами α θ α₂, приведены в таблице 6.

Выводы

1. Для числа π открыт его физический эквивалент α₂ =7,49648184638205•10^-3.

2. Для постоянной тонкой структуры α открыт его геометрический эквивалент π₂=1,83360822(13).

3. Вторая постоянная тонкой структуры α₂ является характеристикой плоского псевдоевклидова пространства.

4. Число π₂ является геометрической характеристикой искривленного пространства.

5. Группа безразмерных констант α, π, α₂, π₂ открывает новые возможности в физической теории. В частности, появились возможности получить теоретическим расчетом константу m_p/m_e, получить простые числовые множители перед большими числами Дирака, получить точные значения больших чисел.

ЛИТЕРАТУРА

1. Дирак П.А.М. Элементарные частицы. М., "Наука",1965, вып.3.

2. Carter J. The Other Theory of Physics, Washington, 1994.

3. Киттель Ч. , Найт У. Рудерман М.: Механика. Берклеевский курс физики." 1, М., "Наука",1975.

4. George Johnson, 10 Physics Questions to Ponder for a Millennium or Two, New York Times, Aug. 15, 2000, p. D3.

5. David Gross, Millennium Madness: Physics Problems for the Next Millenium, Strings 2000 conference at University of Michigan, July 10-15, 2000.

6. Kosinov N. Five Fundamental Constants of Vacuum, lying in the Base of all Physical Laws, Constants and Formulas. “Physical Vacuum and Nature”, N4, 2000, p. 96 - 102.

7. Косинов Н.В. Пять универсальных суперконстант, лежащих в основе всех фундаментальных констант, законов и формул физики и космологии. "Актуальные проблемы естествознания начала века". Материалы Международной конференции 21 - 25 августа 2000 г., Санкт-Петербург, Россия. СПб.: "Анатолия", 2001, с. 176 - 179.

8. Косинов Н.В. Физический вакуум и физика вакуума. "Физический вакуум и природа" №2, 1999, с. 16 - 29.

9. Косинов Н.В. Физический вакуум и гравитация. "Физический вакуум и природа" №4, 2000, с. 40 - 69.

10. А.Пуанкаре. Наука и гипотеза//Пуанкаре А. О науке. М.,1983.

11. Косинов Н.В. Константные базисы физических и космологических теорий. Физический вакуум и природа, N5, 2002, с. 69-104.

12. WWW.lacim.uqam.ca/piData

13. Косинов Н.В. Эманация вещества вакуумом и законы структурогенеза. "Физический вакуум и природа" №1, 1999, с. 82 - 104.

14. Косинов Н.В. Фракталы во внутренней структуре элементарных частиц. Физический вакуум и природа, №3, 2000, с.101-110.

15. П.А.М.Дирак. Космологические постоянные. В книге: “Альберт Эйнштейн и теория гравитации”. М.,Мир,1979.

16. П.Девис. Случайная Вселенная. М.,Мир,1985.