Динамические матрицы

Переводим с английского

Другие статьи автора

---

Win-word.zip

"Геометрия природы фрактальна!"

Бенуа Мандельброт.

ФРАКТАЛ ПРОТОНА - ОСНОВА ЕДИНОГО ГЕНЕТИЧЕСКОГО КОДА СТРОЕНИЯ ВЕЩЕСТВА ВО ВСЕЛЕННОЙ

Косинов Н.В.

E-mail: kosinov@unitron.com.ua

Аннотация

В статье, для исследования особенностей частиц микромира, используются фрактальные структуры. В качестве базовой фрактальной конструкции выбран фрактал протона. Продолжение фрактала протона на очередную стадию структурогенеза естественным образом приводит к фракталам водорода, дейтрона и дейтерия. Фрактал дейтрона позволил получить расчетным путем его массу, значение которой оказалось очень близкой к экспериментальному значению. Фрактальные структуры протона, водорода, дейтрона, дейтерия построены по единому рекурсивному алгоритму. Фрактал протона предлагается рассматривать как фрактальную основу природных структур, как базис единого генетического кода строения вещества во Вселенной.

1. ФРАКТАЛЫ МАТЕМАТИЧЕСКИЕ И ФРАКТАЛЫ ПРИРОДНЫЕ

Понятие "фрактал" было введено Бенуа Мандельбротом в 1975 году. Фрактал, в определении Мандельброта, это структура, состоящая из частей, которые в каком-то смысле подобны целому [2]. Такое определение позволяет охватить наиболее широкое множество объектов, которые подпадают под понятие фрактал. Таким образом, самоподобие является одним из основных признаков фракталов. Небольшая часть фрактала содержит информацию обо всем фрактале.

Подавляющее большинство объектов в природе не могут быть описаны с применением гладких кривых, гладких поверхностей, свойственных привычным геометрическим фигурам. Для описания природных объектов больше подходят недиференцируемые кривые. Если двигаться в сторону меньших масштабов и углубляться в область микромира, то начинают сказываться квантовые проявления в природе. Для такого уровня описания природы гладкие кривые принципиально неприменимы. Мандельброт показал то, что геометрия реального мира не евклидова, а фрактальная. "Правильные" евклидовы объекты являются математической абстракцией, природа же предпочитает негладкие, шероховатые, зазубренные и т.п формы [10]. К евклидовой геометрии и к геометрии Лобачевского-Бойяи добавилась новая геометрия, отличие которой состоит в том, что она не оперирует гладкими объектами и привычными формами типа треугольника, квадрата, круга, шара и т.п. Фракталы остро обнажили то, что не замечалось раньше, а именно, что почти два тысячелетия человечество изучало правильные и гладкие кривые, считая евклидову геометрию геометрией природы. В математике известно, что иррегулярные функции составляют подавляющее большинство по сравнению с непрерывными, гладкими кривыми, поэтому диференцируемость есть нетипичное свойство функций и траекторий [1]. В то же время недиференцируемость является типичным свойством кривых, относящихся к природным объектам. Фрактальная геометрия открывает путь к изучению свойств природных объектов, выражаемых степенными законами.

Фракталы широко представлены как в математике, так и в природе. Фракталы применяются в компьютерной графике, в математике, в механике, в физике. Фракталы стали новым направлением в искустве, демонстрируя собой настоящие шедевры - картины необычайной красоты и привлекательности. Красота фракталов тем более интригующа, поскольку она проявляется на объектах полученных чисто математическими приемами. Фракталы становятся новым инструментом познания мира [2,10,11].

На рис.1 приведена классификация фракталов. В этой классификационной таблице фракталы представлены двумя классами. Один класс представлен "рукотворными" фракталами, другой класс представлен природными фрактальными структурами. К классу "рукотворных" фракталов относятся геометрические, алгебраические и стохастические фракталы. Природные фрактальные структуры представлены физическими фракталами.

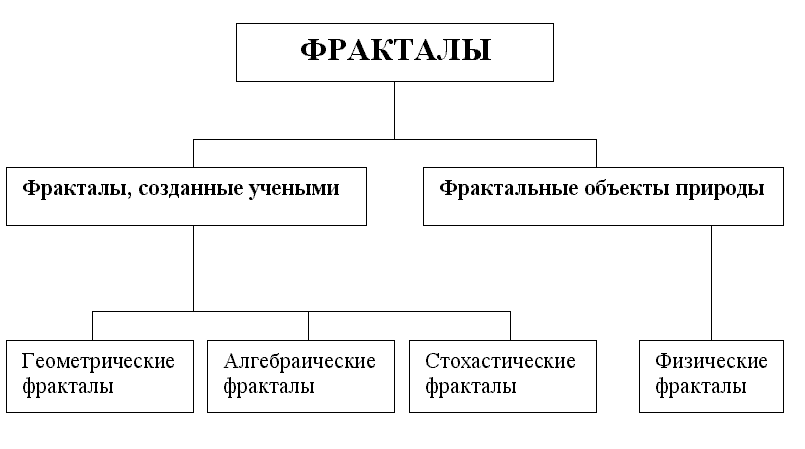
Рис.1. Классификация фракталов.

Геометрические фракталы получают с помощью некоторой ломаной линии или поверхности путем бесконечного повторения процедуры замены отрезков на ломаную-генератор в соответствующем масштабе [11]. Алгебраические фракталы получают с помощью нелинейных процессов в n-мерных пространствах. При этом, очень простые алгоритмы позволяют получать очень сложные структуры, поражающие своей красотой и необычной формой. Стохастические фракталы получаются в том случае, если в итерационном процессе случайным образом менять его параметры [6,11]. Для перечисленных фракталов применима идея бесконечной делимости, что обеспечивает полное самоподобие для математических фрактальных объектов. Однако эти структуры являются идеализированными объектами. Природа же не оперирует бесконечностями. В ней мы не найдем гладких кривых и идеальных объектов. Математические фракталы можно применять к материальным объектам только в качестве моделей - как удобное для расчетов приближение.

Если рассматривать природные фрактальные объекты, то по мере более детального их рассмотрения мы, в конце концов, подойдем к масштабу, где начинают проявляться квантовые эффекты. Это значит, что природные фракталы не имеют бесконечно повторяющихся субструктур и не могут демонстрировать бесконечного самоподобия. В этом состоит особенность природных фракталов. Для природных фракталов в классификационной таблице использован термин - "физические фракталы", чтобы подчеркнуть их "нерукотворность".

2. ПРОТОН - НОСИТЕЛЬ ГЕНЕТИЧЕСКОГО КОДА СТРОЕНИЯ МАТЕРИИ

В [3,4,5] при исследовании структуры протона найдена новая фрактальная структура, которая отражает внутреннее строение и динамику структурогенеза этой частицы. Поскольку протон является основой всех вещественных образований, то закономерности формирования его внутренней структуры должны иметь свое продолжение и в более сложных природных конструкциях. Это породило надежду на возможность раскрытия единого закона структурогенеза вещества - своеобразного гнетического кода Вселенной.

В [3,4] получены свидетельства того, что протон может претендовать на роль носителя генетического кода строения материи. На это косвенно указывает тот факт, что протон является основой всех вещественных образований. По этой же причине фрактал протона должен проявлять себя на макроуровне и, очевидно, может выступать базовой конструкцией для построения различных структур во Вселенной. Если это так , то в протоне могут быть скрыты все основные секреты устройства нашего мира.

Если исходить из идеи единства мира, то закономерности структурогенеза вещества во Вселенной и топологические особенности пространства-времени должны быть напрямую связаны с топологическими особенностями внутренней структуры протона и должны быть основаны на едином рекурсивном алгоритме построения. Есть основания полагать, что фрактальные структуры имеют свое продолжение за пределами элементарных частиц и должны проявляться во всех вещественных формах.

Таким образом, фрактал протона может оказаться самым подходящим объектом для раскрытия генетического кода строения материи. На наш взгляд генетический код строения материи не может содержать только один какой-то признак, например, структурные особенности. Кроме структурных особенностей у этого кода должны существовать еще и динамические признаки. Причем, динамическим признакам должна быть отведена главенствующая роль [3,4]. По нашему мнению, для выявления единого генетического кода строения вещества во Вселенной необходимо решить, по крайней мере, три задачи:

Открыть фрактальный базис структурной организации материи;

Открыть законы структурогенеза вещества и получить их математическое описание.

Открыть алгоритмический базис структурной организации материи;

Как видим, все три задачи непосредственно связаны с проблемами происхождения вещества.

3. ГЕНЕТИЧЕСКИЙ КОД СТРОЕНИЯ МАТЕРИИ

Фундаментальный генетический код строения материи может быть представлен обобщенными динамическими формулами двух видов. Первая формула отражает фрактальные особенности генетического кода Вселенной [3,4]:

P_p =2(...2(2(2(2(2(2(2(2(2(2+1)+1)+1)+1)+1)+1)+1)+1)+1)+... (1)

Эта математическая конструкция названа в [3,4] топологической или фрактальной формулой. В основе фрактальной формулы лежит конструкция вида (2+1), которой соответствует графическая форма (рис.2), названная элементарной ячейкой фундаментального бинарного фрактала[4]:

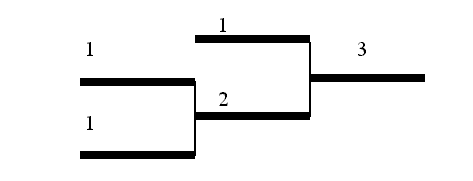
Рис.2. Элементарная ячейка фундаментального бинарного фрактала.

Элементарную ячейку фундаментального бинарного фрактала предлагается рассматривать как основу природных фрактальных конструкций, как фрактальный базис структурной организации материи. Проявление в природе структур, напоминающих элементарную ячейку фундаментального бинарного фрактала можно наблюдать на примере цветков Euphorbia milii, фотографии которых приведены на сайтах: http://filosof.net/disput/kosinov/fp/text.htm ,

http://excluziv.fromru.com/stat/Cosinov/fractal-03.doc на рисунке 6.

Вторая формула отражает закон структурогенеза вещества во Вселенной[3,4]:

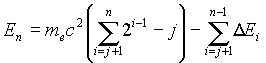(2)

Структурные особенности формул (1) и (2) отображает фундаментальный бинарный фрактал [4]. И для приведенных формул, и для динамической структуры генетического кода имеет место единый алгоритм построения, который представляет собой рекурсивный алгоритм[7]. Рекурсивный алгоритм является алгоритмическим базисом структурной организации материи.

Приведенные выше формулы получены из фрактала протона. Они интересны тем, что являются единственными математическими конструкциями, которые выводят на важнейшую фундаментальную физическую константу - m_p/m_e = 1836,152... и позволяют получить ее расчетным путем. На необходимость выяснения сущности числа 1836,152... и его особенном статусе в физике обращено внимание в [9]. То, что фрактал протона дал возможность получить значение фундаментальной физической константы m_p/m_e, указывает на обоснованность его отнесения к структуре протона.

4. ФРАКТАЛЬНАЯ ДИНАМИКА СТРУКТУРОГЕНЕЗА ВЕЩЕСТВА

Для подтверждения базового статуса фрактала протона рассмотрим, к чему приведет продолжение фрактала протона на следующий уровень структурогенеза. Последовательное продолжение фрактальной формулы протона на очередной шаг и на очередную ступень структурогенеза и оценка количественных характеристик, которые следуют из полученных на каждом шаге фрактальных формул, указывает на то, что новые образования относятся к водороду, дейтрону и дейтерию.

Так, продолжение фрактальной формулы протона на очередной шаг структурогенеза приводит к такой формуле:

P_H =2(2(2(2(2(2(2(2(2(2+1)+1)+1)+1)+1)+1)+1)+1)+1)+1+1

Оценка количественных характеристик, которые следуют из этой формулы, указывает на то, что она относится к водороду. Продолжение фрактальной формулы протона на очередную ступень структурогенеза приводит к такой формуле:

P_d =2(2(2(2(2(2(2(2(2(2(2+1)+1)+1)+1)+1)+1)+1)+1)+1)+1)+1

Оценка количественных характеристик, которые следуют из этой формулы, указывает на то, что она относится к дейтрону.

На рис.3 видно, что продолжение фрактала протона на очередную ступень структурогенеза, естественным образом приводит к фракталу дейтрона. Самоподобие ярко проявляется и на рис.3-а и на рис.3-б.

а). Фрактал протона

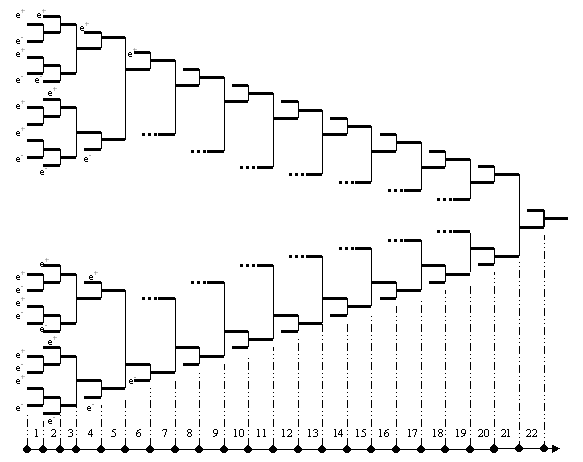
б). Фрактал дейтрона

Рис.3. Фрактал протона (а) и фрактал дейтрона (б).

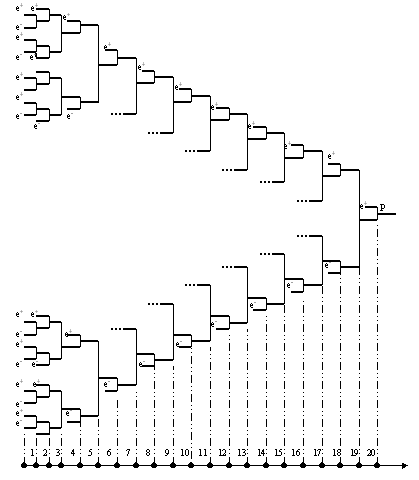
На рис.4 показаны одиннадцать иерархических уровней структурогенеза дейтрона. На одиннадцатой ступени структурогенеза фрактальная субструктура в ином масштабе повторяет самоподобные субструктуры предыдущих ступеней.

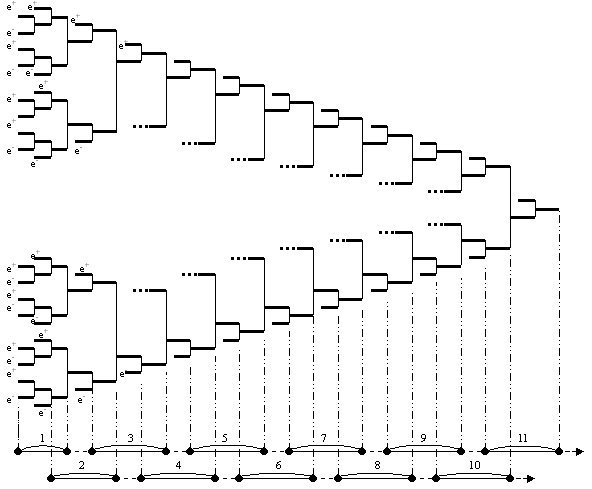
Рис.4. Одиннадцать иерархических уровней структурогенеза дейтрона.

Фрактал дейтрона, как и фрактал протона, следует считать "физическим фракталом", поскольку он представляет собой не бесконечную структуру, а имеет фиксированный масштаб, в котором фрактал завершается на 22-ом шаге структурогенеза вещества и состоит из 11 иерархических уровней, повторяющих структуру элементарной ячейки фундаментального бинарного фрактала. Продолжение фрактальной формулы дейтрона на очередной шаг приводит к такой формуле:

P_D =2(2(2(2(2(2(2(2(2(2(2+1)+1)+1)+1)+1)+1)+1)+1)+1)+1)+1+1

Оценка количественных характеристик, которые следуют из этой формулы, указывает на то, что она относится к дейтерию. Как видим, все фрактальные формулы построены по единому рекурсивному алгоритму. На основании фрактала дейтрона получена формула для расчета массы дейтрона:

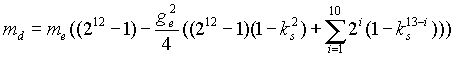(3)

Здесь: g_e - g-фактор электрона, m_e- масса электрона, k_sⁱ - весовые коэффициенты для i-й ступени структурогенеза дейтрона. Значение k_s определяется двумя фундаментальными константами - p (пи) и a (альфа): k_s=f(p, a)=0,9734369645(30) [3,8]. Соотношение (3) приводит к фундаментальной физической константе m_d/m_e , которая до сих пор не находила обяснения и не следовала ни из какой физической теории:

Это значение константы m_d/m_e очень близко к ее экспериментальному значению (CODATA,1998):

m_d/m_e=3670,482955(08).

Второе слагаемое в формуле (3) дает значение дефекта массы частиц-фермионов, участвующих в структурогенезе дейтрона:

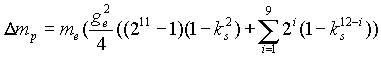(4)

Общий дефект массы складывается из отдельных сотавляющих, которые определяются из фрактала дейтрона. Оценка количественных характеристик фрактала дейтрона приводит к новой фундаментальной константе дейтрона:

Dm_d/m_e=424,517045(08).

Этой безразмерной константе соответствует константа энергии E=216,927743(14) Mev. Это две новые фундаментальные физические константы, которые относятся к дейтрону.

Таким образом, продолжение фрактала протона естественным образом приводит к фракталам других вещественных образований. Изложенное выше указывает на то, что единый генетический код строения материи зашифрован в динамической структуре протона и протон является носителем этого кода. Фундаментальным алгоритмическим базисом строения материи является рукурсия.

Выводы

1. Продолжение фрактальной структуры протона на очередной шаг и на очередную ступень структуризации вещества естественным образом приводит к фракталам водорода, дейтрона, дейтерия.
2. Фрактал дейтрона и фрактальная формула дейтрона отражают закономерность структурогенеза этой частицы и позволяют получить теоретическим расчетом значение фундаментальной физической константы m_d/m_e и предсказать существование новых фундаментальных констант.
3. Фрактал дейтрона, как и фрактал протона, следует считать "физическим фракталом", поскольку он представляет собой не бесконечную структуру, а имеет фиксированный масштаб, в котором структура завершается на 22-ом шаге структурогенеза вещества и состоит из 11 иерархических уровней, повторяющих структуру элементарной ячейки фундаментального бинарного фрактала.
4. Показано, что фрактал протона может быть положен в основу единого генетического кода строения материи. Получены свидетельства того, что генетический код строения материи зашифрован в динамической структуре протона и протон является носителем этого кода. В качестве фундаментального алгоритмического базиса для генетического кода Вселенной предлагается рассматривать рекурсию.

ЛИТЕРАТУРА.

1. Ф.И.Маврикиди. Фракталы: постигая взаимосвязанный мир. Грани науки, 3/2000, стр. 78 - 85.
2. Федер Е. Фракталы. Пер. с англ. -М.: Мир, 1991.
3. Косинов Н.В. Эманация вещества вакуумом и законы структурогенеза. Физический вакуум и природа, N1, 1999, стр.82-104.
4. Косинов Н.В. Происхождение протона. Физический вакуум и природа, N3, 2000, стр.98 - 110.
5. Косинов Н.В. Эманация вещества вакуумом и проблема структурогенеза. Идея, N2, 1994, стр.18-31.
6. Фракталы в физике. Труды 6-го международного симпозиума по фракталам в физике, 1985.
7. Анисимов А.В. Информация. Творчество. Рекурсия. К., "Наукова думка", 1988.
8. Косинов Н.В. Константные базисы физических и космологических теорий. Физический вакуум и природа, N5, 2002, стр.69 - 103.
9. Манин Ю.И. Математика и физика. М. "Знание", 1979.
10.   B.B.Mandelbrot. The Fractal Geometry of Nature, San Francisco: Freeman, 1982.
11. Витолин Д. Применение фракталов в машинной графике. Computer World, 1995, N15.

---

© Косинов Н.В., 2000. При использовании материалов ссылка обязательна.

Публикуется с разрешения автора

Старинные книги