Исследование сетевого трафика
web-ресурса www.energy-links.com
А.В. Жуков, И.В.Аминова
Петрозаводский
государственный университет,
zhukov@karelia.ru, iaminova@karelia.ru
На сегодняшний день
существуют экспериментальные подтверждения о том, что поведение Internet трафика имеет самоподобную (фрактальную)
структуру, [4-7]. Свойство самоподобия характеризуется тем, что при изменении
шкалы измерений корреляционная структура рассматриваемого самоподобного процесса
не изменяется.
В качестве объекта
исследования была выбрана Интернет система Energy-Links.
База данных системы содержит информацию о компаниях работающих в области энергоэффективных технологий Баренцева региона и позволяет эффективно
осуществлять поиск необходимой информации. Это бесплатная система была создана
совместными усилиями Норвежской группы энергоэффективности
(НГЭЭ), Российскими демонстрационными зонами (РусДем),
Центром энергетической эффективности Мурманской области (ЦЭЭМО) и Карельской
Ассоциации энергетической эффективности (КАЦЭЭ). Заинтересованные организации
размещают информацию о себе по адресу в интернете http://www.energy-links.com. На сегодняшний день в базе
данных зарегистрировано более 2000 компаний.
В данной статье
анализируются статистика посещаемости, сведения об объеме информации,
полученной пользователями системы в
период с августа 2001 по июль 2002 года.
Для начала рассмотрим
основные определения. Пусть Z=(Zn, n ≥
0) – стационарный (2-го порядка) процесс в дискретном времени. Построим новый
процесс Zn(m),
получаемый разделением исходного
процесса на блоки размера
m ≥
1, т.е.
Znm +…+Z(n+1)m-1
![]() Zn(m)=
Zn(m)=
mH
- это так
называемый агрегированный процесс.
Процесс Z с математическим
ожиданием EZ1< ∞ и дисперсией DZ1< ∞
называется самоподобным с параметром (Херста) самоподобия
H Є (0, 1), если для каждого m ≥ 1 процессы (Zn(m), n ≥ 0) и (Zn, n ≥ 0) имеют одинаковые конечномерные распределения,
[1].
Таким образом, исходный
процесс и агрегированный процесс имеют одинаковую структуру для любого
параметра шкалы m ≥ 1. Если при этом
ковариационная функция агрегированного процесса не зависит от m, то исходный процесс Z называется самоподобным второго порядка, [1].
В качестве
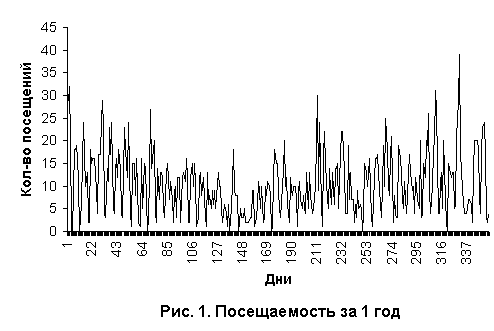
исследуемого объекта мы рассматриваем количество посещений сервера www.energy-links.com
в период с по августа 2001г. по июль
2002г по дням. На рис.1 приведен график посещаемости сервера.
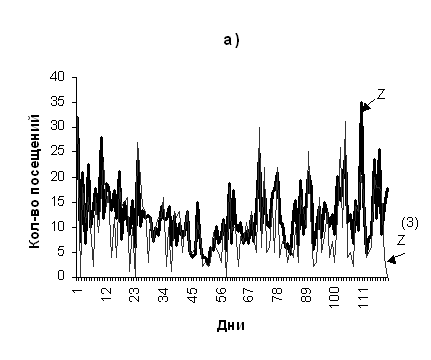
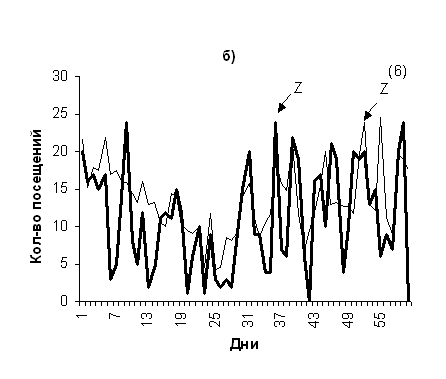
Для проверки процесса посещаемости на самоподобие строятся агрегированные процессы с изменением шкалы. На рис.2 а) и б) изображены графики агрегированных процессов с объединением данных по 3 дня, по 6 дней, соответственно (m=3; 6).
|
|
|
Рис. 2.
Агрегационный процесс Z(m), а) m=3; б) m=6.
При различных параметрах m и H сравнивались
графики агрегированного и исходного процессов посещаемости. Визуально по
графикам было определено, что структура
исходного процесса не нарушается при параметре самоподобия H=0.84.
Таким
образом, мы экспериментально вычислили параметр Н, значение которого находится
в интервале (1/2, 1), что, кроме того,
подтверждает сохранение долговременной зависимости между данными, [1].
Одна
из возможных причин, объясняющих
самоподобную структуру и
долговременную зависимость сетевого трафика, – размеры передаваемых файлов и
количество одновременных подключений имеют распределение с тяжелым хвостом,
[1-3]. Это означает, что эти данные принимают большие значения с достаточно
большими вероятностями, что может приводить
к отказам и замедлению работы сервера.
Будем
говорить, что случайная величина (с.в.) X имеет распределение с тяжелым хвостом, если хвост ее функции распределения имеет следующий вид:
1-F(x) = x - α L(x),
где L(x) – медленно меняющаяся функция, т.е. L(tx)/L(t) →1 при t→∞, для всех x > 0. Наиболее простой случай медленно меняющейся
функции – константа.
Величина α характеризует тяжесть хвоста. Если 0<α<1, то говорят, что F имеет очень тяжелый хвост,
при этом с.в. X имеет бесконечные
математическое ожидание и дисперсию. При
1<α<2 с.в. X имеет
бесконечную дисперсию. Если α>2, дисперсия X конечна.
Существует
несколько методов для оценки тяжести хвоста α по
экспериментальным данным. Предположим для простоты, что L(x)=const. Значение
индекса α можно определить, исходя из соотношения
Ln (1-F(x))
 = - α.
= - α.
Ln (x)
Тогда тангенс угла
наклона линии регрессии,
построенной по группам
данных { Ln ( x ) ; Ln
(1-F(x)) },
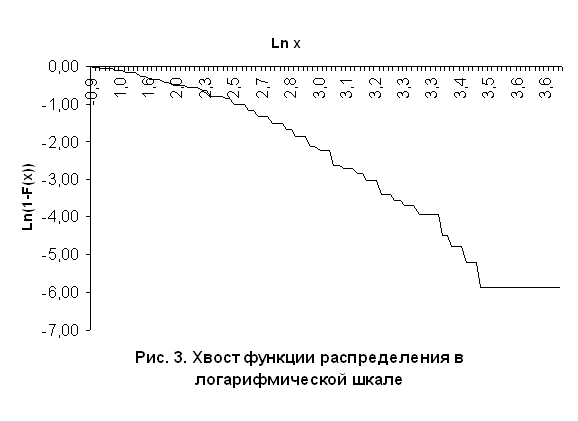
равен значению индекса - α. На рис. 3 приведен
график хвоста эмпирической функции распределения 1-F(x)
в логарифмической шкале, где в качестве исходных данных рассматривались длины
пересылаемых файлов за период с августа 2001г. по июль 2002г.
Вычислив тангенс угла
наклона, мы получили, что индекс тяжести
хвоста α=0.4. Для того,
чтобы убедиться в том, что исследуемая выборка действительно имеет
распределение с тяжелым хвостом с параметром
α= 0.4 мы воспользовались критерием
Колмогорова-Смирнова для проверки гипотезы о виде функции распределения с
уровнем значимости 0.05. Аналогично был вычислен параметр α=0.8
для количества уникальных посещений.
Таким образом, в ходе
исследований выяснено наличие самоподобной структуры с индексом H=0.84 и долговременной
зависимости сетевого трафика www.energy-links.com. Кроме того, было
доказано, что размеры передаваемых файлов через этот web
ресурс имеют распределение с очень
тяжелым хвостом с индексом тяжести хвоста α = 0.4,
а количество посещений - с индексом 0.8.
Литература
[1] I.Aminova Queueing networks
simulation: artificial regeneration and heavy tail phenomena}.\\Proceedengs of
FDPW'99. Petrozavodsk Petrozavodsk State University
[2] H.Drees,
L.Haan, S.Resnick. How to make a Hill plot.
AMS. 1991.
[3] S.I.Resnick.
Heavy tail modeling and teletraffic
data. Ann. Statist. 25:1805-1869. 1997.
[4] S.I.Resnick.,
G.Samorodnitsky. A heavy traffic approximation for
workload processes with heavy tailed service requirements. Management
Science. 46:1236-1248. 2000.
[5] B.K.Ryu.
Fractal network traffic: from understanding to implications. Columbia University
[6] B.K.Ryu.
Fractal network traffic modeling: past, present, and future.1997.
[7] W.Willinger,
V.Paxson, M.Taqqu.
Self-similarity and heavy tails:
structural modeling of networks traffic.// A practical Guide to heavy tails:
statistical
techniques and applications. Boston. 1998.