Самоподобные процессы в коммуникативных сетях

Операции с матрицами на C++. Класс DMatrix

Self-similar processes in communications networks

(Самоподобные процессы в коммуникативных сетях)

Boris Tsybakov, Nicolas D. Georganas, 1998

3. Модель трафика и условия ее самоподобия

В этом разделе будет рассмотрена модель трафика пакетов Y. Модель была предложена в [21], отдельные ее проявления описаны в [7], [10], [13] и [20]. Мы сформулируем условия для строгого и асимптотического самоподобия трафика Y. Похожие концепции в [7], [13], [20] и [21] являются менее общими и подробными. В заключение мы рассмотрим другие известные модели самоподобного трафика.

3.1. Модель трафика пакетов

Рассматриваемый трафик Y будем считать потоком пакетов, имеющих одинаковую длину, принятую здесь за единицу времени. Пакеты связаны с источниками, трафик есть суперпозиция пакетов, генерируемых источниками. Описание структуры трафика начнем с модели источников.

Источники будем нумеровать буквой s. Источник s начинает генерировать пакеты в момент времени ω_s (источники пронумерованы по возрастанию времени, то есть ω_s ≤ ω_s₊₁). Момент времени ω_s будем называть временем появления источника s. Источник s генерирует θ_s(i)∈I₀ пакетов в моменты ω_s + i – 1 в интервале времени ω_s, …, ω_s + τ_s – 1. Последовательность (θ_s(1), …, θ_s(τ_s))называется активным периодом источника s, а τ_s – его длиной. До момента ω_s и после момента ω_s + τ_s – 1 источник s пакеты не генерирует, θ_s(i) = 0 при i < ω_s и при i ≥ ω_s + τ_s. Таким образом, θ_s(t – ω_s + 1), t ∈ I₁ – последовательность количеств пакетов, генерируемых источником s в последовательные моменты времени.

Частными случаями активных периодов, например, могут быть:

1) константа θ_s(i) = R ∈ I₁, 1 ≤ i ≤ τ_s,

2) случайная константа θ_s(i) = R, R зависит от τ_s, то есть R = R(τ_s),

3) независимые и одинаково распределенные θ_s(i), принимающие значения 0 и 1 с вероятностями p₀ и p₁ соответственно,

4) независимые и одинаково распределенные θ_s(i), принимающие значения из множества {0, 1, …, k} с биномиальным распределением или из I₀ с геометрическим, пуассоновским или каким-либо другим заданным распределением,

5) марковские, полумарковские или другие хорошо известные последовательности θ_s(i).

Момент t может быть временем появления сразу для нескольких источников. Пусть ξ_t обозначает число источников со временем появления t. Рассматриваемый трафик Y = (...,Y-1 ,Y0 ,Y1 , ... ) есть суперпозиция пакетов, генерируемых различными источниками:

, .

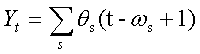Это значит, что Y_t – общее число пакетов, генерируемых источниками, активными в момент t.

Предположим, что:

1. Активные периоды (θ_s(1), …, θ_s(τ_s)) – независимые одинаково распределенные с. в. при различных s, иначе говоря, (τ_s, θ_s(1), …, θ_s(τ_s)) – независимые одинаково распределенные с. в. при различных s. При условии τ_s = l такой период является отрезком стационарного в широком смысле случайного процесса, со значениями из множества неотрицательных целых чисел, определяемого числом l.

2. Количества появившихся источников, ξ_t, t ∈ I_-∞, независимы и имеют одинаковое пуассоновское распределени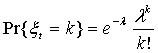е , где - параметр пуассоновского распределения, .

3. Активные периоды (θ_s(1), …, θ_s(τ_s)) (или (τ_s, θ_s(1), …, θ_s(τ_s))) независимы (в совокупности) от чисел ξ_t и моментов ω_s. Числа ξ_t независимы (в совокупности) от моментов ω_s.

В этих трех предположениях заключается специальная модель трафика пакетов Y, которую мы будем рассматривать. В [21] рассмотрен отдельный случай в рамках этой модели, когда периоды (θ_s(1), …, θ_s(τ_s)), τ_s = l для любого s, являются отрезками стационарного в широком смысле случайного процесса, со значениями из множества неотрицательных целых чисел, независимых от l. (Имеется в виду модель Y⁽⁴⁾ из [21]. Вследствие независимости от l модель Y⁽⁴⁾ не может включать в себя модели Y⁽²⁾ и Y⁽³⁾ в качестве частных случаев). Специальный случай нашей модели, а именно - θ_s(i) = 1 для любого i и для любого s рассмотрен ранее в [7], [10], [13], [20].

Y = (…, Y_-1, Y₀, Y₁, …) можно интерпретировать как маркированный точечный процесс с дискретным временем, у которого точками являются s (или ω_s), а метками данной точки s – (τ_s, θ_s(1), …, θ_s(τ_s)) или (θ_s(1), …, θ_s(τ_s)).

Процесс Y может быть разложен с помощью пуассоновского аргумента разложения на бесконечное число независимых процессов Y(l), l ∈ I₁. Частный процесс Y(l) имеет ту же структуру, что и процесс Y, но с заданной длиной активного периода τ_s = l для всех его источников и с количеством источников, появившихся за время t, равным ξ_t_,_l – пуассоновской случайной величине с параметром λ_l = E ξ_t_,_l = λ Pr(τ = l), где τ – символ, обозначающий τ_s в процессе Y.

Иначе говоря:

, , .

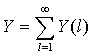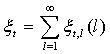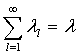Можно представить себе это разложение следующим образом. В момент появления каждый источник отправляется к процессу Y(l) с вероятностью Pr(τ_s = l)независимо от других источников и от времен их прибытия. Если источник s отправлен к Y(l), то τ_s = l и этот источник имеет распределение, полученное из распределения для (θ_s(1), …, θ_s(τ_s)) у процесса Y при условии τ_s = l в качестве безусловного распределения активного периода у процесса Y(l).

В следующем пункте мы будем использовать разложение процесса Y для получения условий его самоподобия.

3.2. Условия самоподобия трафика Y

Наша цель – получить условия, при которых описанный в пункте 3.1 трафик пакетов самоподобен.

………………………………………………………………………………………………..

< далее не переведено >

ОГЛАВЛЕНИЕ

ЧИТАТЬ СТАТЬЮ ПОЛНОСТЬЮ