Операции с матрицами на C++.
Класс DMatrix
VORTEX RINGS
ВИХРЕВЫЕ КОЛЬЦА
(или ТОРОИДАЛЬНЫЕ ВИХРИ)
Karim Shariff, Anthony
Leonard
(1992)
1 .
CONTEXT AND CONTENT
To
interest an engineer in vortex rings one might cite the fact that cavitated rings are used for underwater drilling (Chahine & Genoux 1983), have
potential use in fighting oil well fires (Akhmetov
1980) and are used in modeling the downburst, a hazard to aircraft (Lundgren et
aI 1991). With a physicist one could reason that
vortex rings (along with helical vortex tubes and kink waves) admit invariant
states and therefore are candidates for "elementary excitations" in
turbulence, and one could mention that accelerating ions in superfluid helium
create quantized vortex rings (Rayfield & Reif 1963). To a natural philosopher one could explain how
dolphins blow vortex ring bubbles and swim through them for amusement (Lundgren
& Mansour 1991) and how drops falling into a glass of water form vortex
rings. While these are all reasons for making one enchanted with vortex rings,
the enduring value of studying them lies elsewhere. One need only look at work
of the last century, directed towards proving Kelvin's theory of vortex ring
atoms, or at work of two decades ago, sometimes interested in whether vortex
rings could be employed to launch pollution wastes to higher altitudes, to see
that what survives time are the purely hydrodynamic results concerning the
behavior of vorticity and the specific examples that
enrich our intuition about vorticity. That the vortex
ring has been used to understand various aspects of vortex motion is due to the
fact that it is fairly robust, as well as simpler to generate, analyze, and
isolate from end-effects than other configurations.
1 . КОНТЕКСТ И СОДЕРЖАНИЕ
Объяснить интерес инженеров к
вихревым кольцам можно тем, что кавитирующие кольца, возникающие при подводном
бурении (Chahine & Genoux
1983),
потенциально могут быть использованы для борьбы с возгораниями на нефтяных
скважинах (Akhmetov 1980),
или тем, что с их помощью моделируются нисходящие потоки воздуха,
представляющие опасность для воздушных судов (Lundgren et al 1991). Для физика интерес обусловлен тем,
что вихревые кольца (и спиральные вихри, и изгибные волны) считаются
инвариантными структурами и, следовательно, кандидатами в «элементарные
возбуждения» при турбулентности; также можно вспомнить, что ускоряющиеся ионы
гелия в сверхтекучем состоянии формируют вихревые кольца (Rayfield & Reif 1963).
Естествоиспытатель подумает о пузырях в форме вихревых колец, которые для
развлечения выдувают дельфины и проплывают сквозь них (Lundgren & Mansour 1991) и о том, как капли,
падая в стакан с водой, принимают форму все тех же колец. Все эти проявления
вихревых колец очаровывают нас, но главная задача изучения феномена заключается
в другом. Необходимо лишь обратиться
к работам прошлого века, базирующимся на теории Кельвина об атомах – кольцевых
вихрях, или к работам двадцатилетней давности, в которых иногда высказывалось
предположение о том, что вихревые кольца играют роль в резком усилении
загрязнения бытовыми отходами, чтобы увидеть, что с течением времени важнейшими
остаются чисто гидродинамические результаты, относящиеся к поведению вихрей, и
специфические примеры, улучшающие наше интуитивное понимание данного
феномена. Таким образом, вихревые кольца
нужны для осознания различных аспектов вихревого движения, чему способствуют
четкость его проявления, легкость генерации и исследования, отсутствие краевых
эффектов, чего нельзя сказать о других структурах.
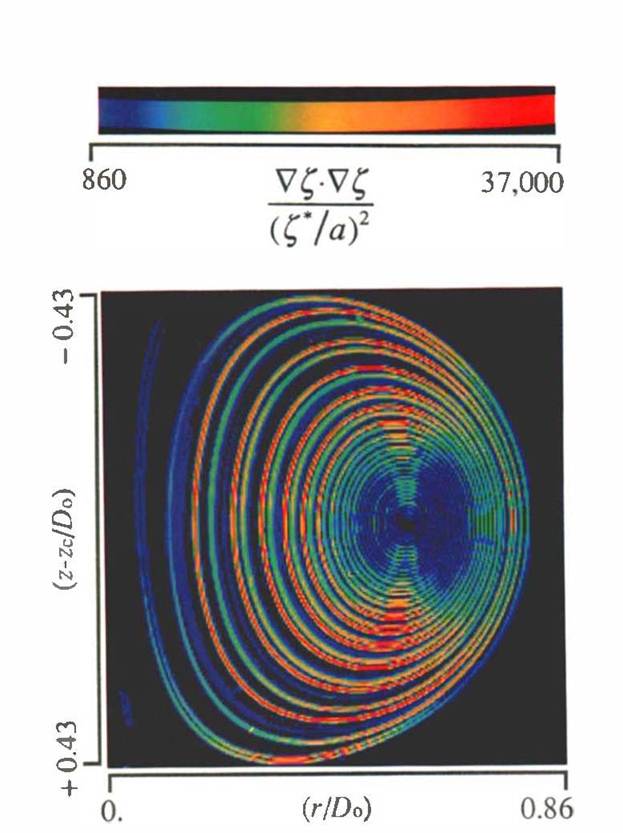
Figure
1. From Southerland et al (1991). Shown is the mixing
rate of a tracer in a well-developed laminar vortex ring. The tracer is a dye
of Schmidt number ≈ 600 injected into the pipe fluid. The measure of
mixing rate depicted is ∇c * ∇c, where c(x, σ) is the
concentration field. Notice how the mixing rate diminishes towards the vortex center. This is because
adjacent diffused layers have begun to overlap. Contrast this with measurements
(Dabiri & Gharib 1991)
employing a low Schmidt number tracer (temperature).
Рис
1. Из работы Southerland
и др. (1991). Показана степень смешения трассера в устоявшемся ламинарном
вихревом кольце. В качестве трассера использована краска с числом Шмидта ≈
600, впрыснутая в трубку тока жидкости. Степень смешения показана как∇c * ∇c,
где c(x, σ) – поле концентрации.
Обратите внимание,
как смешивание
уменьшается по направлению к центру вихря.
Это происходит
потому, что соседствующие слои
с краской
начинают сливаться. Что контрастирует с
измерениями (Dabiri
& Gharib 1991),
в которых использовался трассер (температурный) с маленьким числом Шмидта.
CONTEXT
КОНТЕКСТ
In
recent years, vortex rings have been studied in the broader arena of three
issues.
В последние годы вихревые
кольца изучались в широком круге задач, принадлежащем к трем разным
направлениям.
1.
Generation of sound.
One
probably intuitively appreciates the role vortices play in the generation of
sound – according to a linguist (Minahen 1983),
"the words 'whirl' and 'whorl,' associated with the vortex, for example
the breathy 'wh' in combination with the churning 'rl' indicates something more than simply an arbitrary
relationship between the idea and its acoustical image." Moehring (1978) expressed the (quadrupole)
sound field directly in terms of vorticity
unsteadiness and this led Muller & Obermeier
(1988) to take D. Kuechemann's (1965) statement that
vortices are the "muscles and sinews" of fluid motion and add that
vortices might also be called the "voice of the flow." In aeroacoustic experiments it is often difficult to pinpoint
individual events as sound sources. Kambe, Minota and their co-workers have been studying the
acoustics of mutually interacting rings and rings interacting with edges and
bluff bodies (see Minota et al 1988 and references
therein). Because their experiments permit identification of the sound source
and have often accompanied successful theoretical modeling, theirs has been
rightly hailed as one of the few "clean" aeroacoustic
experiments.
1. Генерация звука.
Возможно, интуитивно придается
большое значение той роли, которую вихри играют в образовании звука – согласно
мнению лингвиста (Minahen 1983),
"в словах 'whirl' и 'whorl,' связанных по смыслу с вихрем,
придыхательное 'wh' в
сочетании с клокочущим 'rl' указывают на нечто большее,
чем просто произвольную связь между концепцией и ее звуковым образом". Moehring (1978)
представил квадрупольное звуковое поле непосредственно в терминах вихревой
зыби, это заставило Muller’а
& Obermeier’а
(1988) взять высказывание D. Kuechemann’а (1965)
о том, что вихри - это "мускулы и жилы" движения жидкости и добавить,
что водовороты можно назвать еще "голосом потока". В экспериментах по
аэроакустике часто бывает нелегко распознать
отдельные источники звука. Kambe, Minota и их
сотрудники изучали акустику попарно взаимодействующих колец и колец,
взаимодействующих с кромками поверхностей и плохообтекаемыми телами (см. Minota
et
al (1988)
и статьи по ссылкам оттуда). Так как их эксперименты делают
возможной идентификацию источника звука и их результаты часто хорошо совпадают
с теоретическим моделированием, они признаны «чистыми» аэроакустическими
экспериментами.
2.
Transport and mixing.
We
also recognize, through our everyday experiences, the role of vortices in
mixing. Dimotakis (1984) for instance, describes
mixing in shear layers as a two step process:
engulfment by the Biot-Savart induced velocity
followed by straining of interfaces between species and molecular diffusion.
Both steps are exemplified in vortex rings. With respect to the first step, there
are two forms of engulfment. One form is that exhibited by any temporally or
spatially growing region such as a jet (Taylor 1958). Specifically, a viscous
vortex ring carries with it a continually increasing volume of fluid and while
this process can be visualized in the limit of self-similar decay (Allen 1984,
Cantwell 1986), only a simple model has been constructed for earlier times (Maxworthy 1972, 1974). The mechanism of growth need not be
viscous-this form of entrainment is also present in rings expanding due to
buoyancy (Turner 1963) and in the growing spiral vortex sheet during ring
formation. After formation, the vortex consists of certain fractions of
effluent and ambient fluid (Auerbach 1988). The
second form of engulfment arises from vorticity
fluctuation. It is illustrated by turbulent vortex rings. Unsteadiness of the vortical core causes ambient fluid to be engulfed into the
"atmosphere" of fluid transported with the ring, in exchange for old
fluid. This process can be studied for simple models of vortex pairs and rings
using dynamical systems theory (Rom-Kedar et al 1990,
Shariff et al 1989).
2. Транспортировка и
перемешивание.
Исходя из нашего практического
опыта, мы можем оценить роль вихрей в перемешивании. Dimotakis (1984), например, описывал
перемешивание в пограничном слое как двухшаговый
процесс: захват (со скоростью, определяемой законом Био-Савара),
за которым следует напряжение на поверхностях раздела сред и молекулярная
диффузия. В вихревых кольцах присутствуют оба этих шага. Что касается первого
шага, существует два вида захвата. Первый вид представлен какими-либо
всплесками струйного типа (Taylor 1958).
Точнее говоря, вязкое вихревое кольцо захватывает постоянно возрастающий объем
жидкости и, так как этот процесс можно представить себе как предел самоподобного затухания (Allen 1984, Cantwell 1986), до сих пор получалось
построить только простую модель такого процесса (Maxworthy 1972, 1974). Механизм роста не обязан быть вязким – этот вид захватывания также
представлен кольцами, расширяющимися с помощью подъемной силы (Turner 1963), и растущей
спиральной вихревой пеленой, формирующей кольцо. Сформировавшийся вихрь
состоит из истекающих и захватываемых частей (Auerbach 1988).
Второй вид захвата случается при
вихревых пульсациях. Он представлен турбулентными вихревыми кольцами.
Неустойчивость центра водоворота приводит к втягиванию «внешней» части жидкости
в «атмосферу» движущегося вихря и обмену веществ между вихрем и средой. Этот
процесс можно изучать на простых моделях пар вихрей и колец с помощью теории
динамических систем (Rom-Kedar
et al 1990, Shariff
et al 1989).
Measurements
illustrating the second step of mixing (straining and molecular diffusion) are
shown in Figure 1 for the post roll-up phase of a laminar vortex ring. Johari (1990) has performed preliminary experiments of
chemical reactions for turbulent rings.
Результат опыта,
иллюстрирующего второй шаг перемешивания (напряжение и молекулярная диффузия)
показан на рис. 1 для фазы после свертывания в ламинарном вихревом кольце. Johari
(1990) провел предварительные опыты с химическими реакциями в турбулентных
кольцах.
3.
Vortex interactions.
The
interaction of vortex tubes is a very complex problem without constraining
symmetries. It involves core deformation, vorticity
cancellation/merging, change of topology of vortex lines, and intense vorticity stretching. This review discusses axisymmetric
(coaxial) interactions and is therefore limited to the first two issues. A
vortex near a no-slip wall can create very intense vorticity
in the unsteady boundary layer. This vorticity may
separate to form other secondary vortices. Production of secondary vorticity reduces the vorticity
flux into bluff body wakes and may be the progenitor of "bursting" in
the turbulent boundary layer (Robinson 1991).
3.
Взаимодействие вихрей
Взаимодействие вихревых трубок
– довольно сложная проблема, если рассматривать ее без ограничений на
симметрию. Эта проблема включает в себя деформации ядра, гашение/растворение завихренности, изменение топологии вихря и сильное его
растяжение. Мы рассмотрим только осесимметричные (коаксиальные) взаимодействия,
и, таким образом, ограничимся первыми двумя составляющими проблемы. Вихрь,
оказавшийся рядом со поверхностью, у которых
практически отсутствует проскальзывание, может вызвать очень сильную завихренность в неустойчивом пограничном слое. Эта завихренность может приводить к формированию новых вихрей.
Образование вторичной завихренности
редуцирует вихревой поток в направлении следа плохообтекаемого тела и может
порождать «взрывчатость» в турбулентном пограничном слое (Robinson 1991).
CONTENT
СОДЕРЖАНИЕ
Saffman (1981), in encapsulating the vortex ring problem,
said that "one particular motion exemplifies the whole range of problems
of vortex motion and is also a commonly known phenomenon, namely, the vortex
ring. … Their formation is a problem of vortex sheet dynamics, the steady state
is a problem of existence, their duration is a problem of stability, and if
there are several we have a problem of vortex
interactions." We shall do our best to follow this paradigm in organizing
this article but sometimes we are forced to a make a division along viscous/inviscid lines. The next section focuses on the problem of
formation by discussing how rings are generated naturally and in the
laboratory, their resulting structure, and finally, what factors determine
whether the rings are laminar or turbulent. Section 3 describes three stages in
the life of a laminar ring. Section 4 discusses inviscid
dynamics and begins with a discussion of how core dynamics influences overall
ring motion (Section 4.1). There are examples of laminar vortices in two
dimensions, which attain a balance of nonlinear terms in the inner core; the
suggestion that this may be also true of laminar rings is a thread that
connects laminar rings to Section 4.2, which discusses the theory of inviscid
steady-state rings. Largely however, this body of work stands apart. Unsteady
inviscid effects such as mutual straining are discussed in Section 4.3.
Saffman (1981), формулируя проблему
вихревых колец, сказал: «отдельно взятое движение представляет целый набор
проблем вихревого движения, а также хорошо известного феномена – вихревого
кольца. … Их формирование – вопрос динамики вихревой пелены, устойчивое
состояние – вопрос существования, время жизни – вопрос стабильности, а если они
различны – возникает вопрос взаимодействия вихрей.» Мы
будем стараться следовать этой парадигме при написании данной статьи, но иногда
будем вынуждены делать различие между вязкими и невязкими линиями. Следующая
глава статьи посвящена проблеме формирования; в ней мы рассмотрим, как
формируются кольца в реальной жизни и в лабораторном эксперименте, рассмотрим
структуру получившихся колец и, наконец, факторы, определяющие их ламинарность
или турбулентность. В 3-й главе описаны три стадии жизни ламинарного кольца. В
4-й главе обсуждается невязкая динамика и начинается разговор о влиянии
динамики ядер на движение колец в целом (пункт 4.1). Приведены примеры двумерных ламинарных вихрей,
достигающих равновесия нелинейных членов для внутреннего ядра; предположение,
что это может быть верным и для ламинарных колец, приводит нас к пункту 4.2,
где рассматривается теория невязких устойчивых колец. Важно отметить, что эта
часть работы стоит особняком. Неустойчивые невязкие эффекты, например, взаимная диффузия поверхностей, рассмотрена в пункте 4.3.
И
т.д. …