В "Википедии" нашелся алгоритм сложности O(Nlog2N)для произвольного N.
Алгоритм основан на значительном увеличении числа элементов последовательности и дополнении ее нулями. Хотя такое
расширение, естественно, будет компенсироваться высокой скоростью алгоритма.
Длина последовательности берется равной N', где N' - степень двойки ближайшая сверху к
2N. То есть, 4N > N' = 2T ≥ 2N. Т.е. число элементов новой последовательности
в худшем случае может превышать число элементов исходной последовательности почти в 4 раза.
Например, если N = 9, то N' = 32.
Обозначим
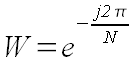
Представим формулу (1) в виде:
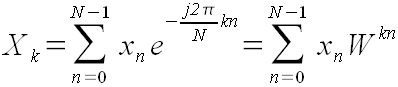
Преобразуем степень:
kn = 2kn/2 = (−k2 + k2 + 2kn + n2 − n2)/2
= (−k2 + (k + n)2 − n2)/2
Это используем для дальнейшего преобразования формулы (1):
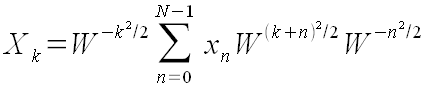
Далее введем обозначения:
x'n = xnW −n2/2
X'k = XkW k2/2
Для n > N, полагаем xn = 0.
Тогда
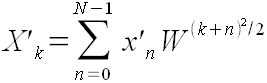 (42)
(42)
И далее авторы алгоритма выполняют виртуозный "финт ушами". Пусть:
zk = (2N − 2 − k)
wn = W zn2/2
И превращают формулу (42) в:
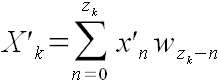 (43)
(43)
Проверим:
wzk − n
= W (zzk − n)2/2
= W (2N − 2 − (zk − n))2/2
= W (2N − 2 − zk + n)2/2
= W (2N − 2 − (2N − 2 − k) + n)2/2
= W (2N − 2 − 2N + 2 + k + n)2/2
= W (k + n)2/2
Правая часть формулы (43) является дискретной сверткой. В общем случае формула свертки имеет вид:
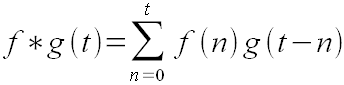 (44)
(44)
где f и g - функции от целых переменных (т.е. дискретные функции). В данном случае
роль таких функций играют x'n и wn,
которые "зависят" от своих индексов как от целых переменных. Свертка обладает замечательным
свойством:
F(f * g) = F(f) F(g) (45)
где F(f) - это дискретная функция, которая получается из дискретной функции f
с помощью быстрого преобразования Фурье.
Дальнейший порядок вычисления таков. Сначала надо вычислить F(x'), то есть
взять набор x'n и вычислить БПФ для n = 0...N' − 1.
Затем вычислить F(w), для чего взять набор wn и вычислить
БПФ для n = 0...N' − 1. Потом по формуле (45) простым перемножением получаем
F(x' * w) = F(x') F(w). Просто берем i-й элемент, полученный после
БПФ набора x'n, и умножаем на i-й элемент, полученный после
БПФ набора wn. В результате получим БПФ свертки x' * w.
Теперь у нас есть БПФ свертки, из него надо получить саму свертку. Для этого применяем обратное
преобразование Фурье. Теперь нам надо найти X'k. Для этого используем формулу
(43). k-й элемент набора Xk будет соответствовать
zk-му элементу свертки. Наконец, останется перейти от X'k
к Xk.
В процессе вычислений мы применяли алгоритмы порядка сложности N, N' и N'log2N'
(когда делали три БПФ).
Поскольку N' не может превышать N более, чем в 4 раза, то весь алгоритм
имеет сложность O(Nlog2N)
Обратное преобразование требует величины W без минуса в показателе и в конце алгоритма - деления
всех полученных элементов на N. Три алгоритма БПФ остаются в этом случае теми же: два прямых
перобразования и одно обратное.
На следующей страничке приведен листинг программы, выполняющей прямое и обратное преобразования
по этому алгоритму. Оптимизация выполнена примерно теми же способами, что и в предыдущем случае
с незначительными модификациями. Переменные x' в алгоритме обозначаются как x_,
2N как N2, N' как N_,
zk как N22, π/N (или
−π/N при обратном преобразовании) как piN.
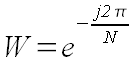
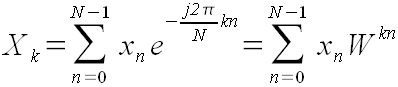
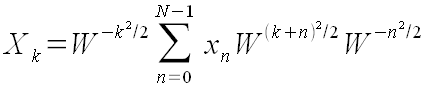
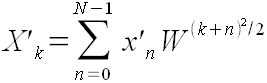 (42)
(42)
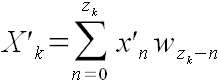 (43)
(43)
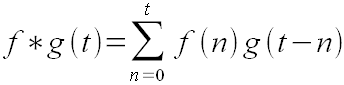 (44)
(44)