В приведенной выше программе велико искушение для вычисления поворачивающих множителей использовать формулу:
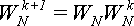 . (17)
. (17)
Это позволило бы избавиться от возведений в степень и обойтись одними
умножениями, если заранее вычислить
Этого можно было бы избежать, будь число
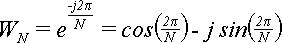
Как же избежать множества обращений к весьма медленным функциям синуса и косинуса? Здесь нам приходит на помощь давно известный алгоритм вычисления степени через многократные возведения в квадрат и умножения. Например:
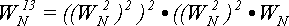
В данном случае нам понадобилось всего 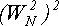 не нужно вычислять
дважды) вместо
не нужно вычислять
дважды) вместо
Можно сократить вдвое количество умножений на каждом шаге, если использовать результаты прошлых вычислений
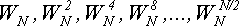 ,
,
для хранения которых нужно дополнительно
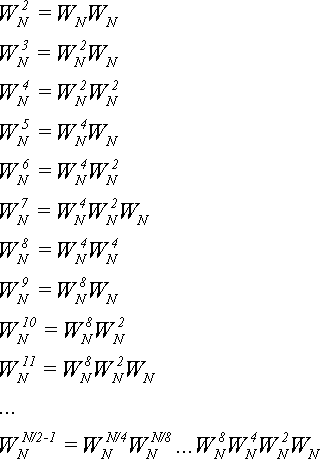
Если очередное 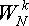 не было вычислено
предварительно, то берется двоичное представление
не было вычислено
предварительно, то берется двоичное представление 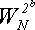 , который хранится
в
, который хранится
в
Есть способ уменьшить количество умножений для вычисления
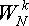 до одного на два цикла. Но для
этого нужно отвести
до одного на два цикла. Но для
этого нужно отвести 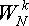 . Алгоритм достаточно
прост. Нечетные элементы вычисляются по формуле (17). Четные вычисляются по
формуле:
. Алгоритм достаточно
прост. Нечетные элементы вычисляются по формуле (17). Четные вычисляются по
формуле:
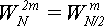
То есть, ничего не вычисляется, а берется одно из значений, вычисленных
на предыдущем шаге, когда
И последние пояснения относительно листинга.
Во-первых, здесь присутствует реализация простейших операций над комплексными числами (классы Complex и ShortComplex), оптимизированная под данную задачу. Обычно та или иная реализация уже есть для многих компиляторов, так что можно использовать и ее.
Во-вторых, массив
В-третьих, для вычислений используются наиболее точное представление чисел с плавающей точкой в C++: long double размером в 10 байт на платформе Intel. Для хранения результатов в массивах используется тип double длиной 8 байт. Причина - не в желании сэкономить 20% памяти, а в том, что 64-битные и 32-битные процессоры лучше работают с выровненными по границе 8 байт данными, чем с выровненными по границе 10 байт.