MDX – язык запросов к многомерным базам данных

Переводим с английского (математика)

Другие книги и статьи Антонова В.М.

---

Антонов В.М.

Физика

Русский вариант

Учебник 3 – Физика вычислительная

2008 год

В основу учебника положена Русская теория эфирной физики, согласно которой эфир является тем протовеществом, из которого построен весь видимый нами мир.

Учебник нацелен на объяснение всех физических процессов и явлений с учётом элементарного строения вещества.

В третьем учебнике произведены расчёты численных значений физических величин.

© Антонов Владимир Михайлович

Содержание

Напоминание

1. В предыдущем учебнике

Эфир является светонесущей средой. Он заполняет всё то пространство – вокруг нас и вплоть до далёкого космоса, - которое мы наблюдаем.

Элементарная частица эфира – ничтожно малый идеальный шарик.

Эфирная среда очень сильно сдавлена.

Всё видимое нами пространство представляет собой единое скопление эфира. Называется это скопление Метагалактикой; она – наша, родная, поэтому будем писать её с большой буквы.

За её пределами – пустота.

В той пустоте блуждают другие скопления эфира, другие метагалактики.

Все вместе они образуют Вселенную.

Иногда метагалактики сталкиваются между собою. Фронты столкновений образуют всевозможные космические завихрения эфира, называемые галактиками.

Наша родная Галактика (будем её также писать с большой буквы) – Млечный Путь. На окраине Млечного Пути располагается Солнечная система; в её составе – наша Земля.

При столкновении метагалактик возникают химэлементы.

Они представляют собой микроскопические торовые вихри в эфирной среде. В сечении торового вихря – три эфирных шарика. Каждые такие три эфирных шарика образуют электронную секцию вихря.

Наглядной моделью торового вихря является кольцо большого диаметра из тонкой упругой проволоки.

Эфирная среда сминает торовые вихри и свёртывает их в различные фигуры. Чем больше диаметр торового вихря, тем сложнее фигура.

У свёрнутого торового вихря образуются петли и жёлобы. И у петлей и у жёлобов одна сторона – присасывающая.

Химэлементы соединяются между собой петлями и желобами.

При ударе по химэлементу он начинает звенеть. Звенят отдельные участки торовихревого шнура химэлемента; эти участки колеблются как струны.

Струнные колебания являются тепловыми колебаниями химэлементов. Звон этих колебаний мы не можем услышать (их частота колебаний очень и очень большая), но чувствуем их наощупь – они воспринимаются как тепло.

Струнные колебания возмущают прилегающий эфир; эти возмущения имеют вид волн. Эти волны не уходят в пространство, а остаются возле своих источников. Это – тепловые волны химэлементов. Эти волны являются как бы тепловыми оболочками химэлементов, препятствующими их сближению в газообразном состоянии.

Как только размах струнных колебаний достигает определённого порога, тепловая волна срывается со струны и уходит в пространство.

Распространяющиеся в эфире тепловые волны являются светом.

Торовые вихри химэлементов могут быть разорваны и рассеяны.

Разорванные химэлементы очень опасны для здоровья людей.

Мириады химэлементов, возникающих при столкновениях метагалактик, слипаются и образуют планеты.

Распад химэлементов разогревает планеты и превращает их в звёзды.

Солнце когда-то было громадной планетой, расколовшейся позднее на куски. Оголившееся раскалённое ядро Солнца стало светиться как звезда.

Земля – один из кусков, отколовшихся от Солнца.

Электрон – элементарный обрывок торовихревого шнура химэлемента. Электроны могут восприниматься как пыль химэлементов.

Электрон является элементарным магнитиком. Собранные соосно электроны образуют магнитный шнур, а собранные в пучок магнитные шнуры образуют магнитный сноп.

2. Некоторые физические величины

Физическая величина		Обозначение и зависимость		Единица измерения
				Название		Обозначение и размерность
Основные физические величины
Линейный размер		l , b, h, δ		метр размерный		мр
Путь		s		метр пути		мп
Инерция		I		ин		ин
Продолжитель ность		t		секунда		с
Поворот (вращение)		φ, (m)		градус, радиан, (оборот)		град, рад, об
Производные физические величины
Площадь			кваметр		квм = мр^2
Объём размерный	V = l*b*h		кубометр размерный		кбм = мр^3
Объём энергетический	g = S*s		кубометр энергетич.		кбм = мр^2*мп
Плотность инерции			пин
Скорость			скор
Ускорение			ускор
Усилие			сила
Удельное давление			уддав
Уклон удельного давления			уклон
Энергия движений			движ
Энергичность			мощность
Температура			терм
Скорость поворота (вращения)			скор поворота
Ускорение Поворота (вращения)			ускор поворота (вращения)
Усилие поворота			сила поворота
Инерция поворота			ин поворота
Энергия вращения			движ
Период колебаний			секунда колебания
Частота колебаний			колебан
Длина волны			метр

Вычисления

1. Точность вычислений

Все вычисления в учебнике – приблизительные. Цель учебника – не получить максимально точное численное значение физической величины, а определить её такой, какая позволяет нарисовать общую картину физического мира.

Примеры.

Диаметр эфирного шарика равен 2,44*10^-13 м. Его численное значение говорит о том, что он гораздо меньше самых малых частиц химических веществ.

Удельное давление эфирной среды составляет 1,70*10²⁴ уд. Это давление превосходит все известные удельные давления материалов и сред на несколько десятичных порядков.

Для профессиональных целей все вычисления данного учебника должны быть уточнены.

2. Эфирный шарик как фундаментальная единица измерений

Учитывая то, что всё в этом мире построено из эфирных шариков, к ним должно быть особое отношение.

В частности, как исключительные должны восприниматься параметры этих шариков.

Основанием для этого служит то, что эфирные шарики никогда и ни при каких обстоятельствах не изменяются ни в размерах и ни в качестве; они вечны и неизменны; и все шарики – абсолютно одинаковые.

Поэтому их параметры могут считаться фундаментальными физическими константами.

Такими константами являются:

· диаметр эфирного шарика;

· инерция эфирного шарика.

Исходя из этого, эфирный шарик может использоваться как фундаментальная единица измерений:

· фундаментальная единица измерений линейного размера – диаметр эфирного шарика; обозначение единицы – дш;

· фундаментальная единица измерений инерции – инерция эфирного шарика; обозначение единицы – инш.

На практике в качестве единиц измерения линейных размеров и инерций используются международные эталоны:

· метр-эталон для измерения линейных размеров; обозначение метр-эталона – мр; соотношение с эфирным шариком: 1 мр = 4,10*10¹² дш;

· ин-эталон для измерения инерций; обозначение ин-эталона – ин; соотношение с инерцией эфирного шарика: 1 ин = 5,49*10³⁰ инш.

3. Инерция эфирного шарика

Из экспериментальной физики известно, что инерция электрона I_Э = 9,1*10^-31 ин.

Электрон представляет собой волчок из трёх эфирных шариков с двумя осевыми шариками. Всего в электроне – 5 эфирных шариков.

Разделим инерцию электрона на 5 и получим инерцию эфирного шарика:

.

Инерция эфирного шарика не возникает, не изменяется и не исчезает; она – неотъемлемое и неизменное свойство эфирного шарика.

4. Инерция электронной секции вихревого шнура химэлемента

В электронной секции насчитывается три эфирных шарика.

Её инерция составляет:

.

5. Инерции титульных химэлементов

Протий P:

Титульное количество электронных секций = 3100.

Инерция:

I_P = 5,46*10^-31*3100 = 1,69*10^-27 ин.

Дейтерий D:

Титульное количество электронных секций = 6100.

Инерция:

I_D = 5,46*10^-31*6100 = 3,33*10^-27 ин.

Тритий T:

Титульное количество электронных секций = 9200.

Инерция:

I_T = 5,46*10^-31*9200 = 5,02*10^-27 ин.

Гелий He:

Титульное количество электронных секций = 12200.

Инерция:

I_He = 5,46*10^-31*12200 = 6,66*10^-27 ин.

Литий Li:

Титульное количество электронных секций = 21100.

Инерция:

I_Li = 5,46*10^-31 *21100 = 1,15*10^-26 ин.

Бериллий Be:

Титульное количество электронных секций = 27400.

Инерция:

I_Be = 5,46*10^-31*27400 = 1,50*10^-26 ин.

Бор B:

Титульное количество электронных секций = 32900.

Инерция:

I_B = 5,46*10^-31*32900 = 1,80*10^-26 ин.

Углерод C:

Титульное количество электронных секций = 36500.

Инерция:

I_C = 5,46*10^-31*36500 = 1,99*10^-26 ин.

Азот N:

Титульное количество электронных секций = 42600.

Инерция:

I_N = 5,46*10^-31*42600 = 2,33*10^-26 ин.

Кислород O:

Титульное количество электронных секций = 48600.

Инерция:

I_O = 5,46*10^-31*48600 = 2,65*10^-26 ин.

Фтор F:

Титульное количество электронных секций = 57700.

Инерция:

I_F = 5,46*10^-31*57700 = 3,15*10^-26 ин.

Неон Ne:

Титульное количество электронных секций = 61300.

Инерция:

I_Ne = 5,46*10^-31*61300 = 3,35*10^-26 ин.

Натрий Na:

Титульное количество электронных секций = 69900.

Инерция:

I_Na = 5,46*10^-31*69900 = 3,82*10^-26 ин.

6. Длина вихревого шнура химэлемента протия в единицах дш

По длине шнура отдельная электронная секция занимает место одного эфирного шарика. Следовательно, длина шнура в единицах дш численно равна количеству электронных секций данного химэлемента.

У титульного химэлемента протия – 3100 электронных секций; значит, длина его вихревого шнура составляет:

.

7. Диаметр химэлемента протия в единицах дш

Химэлемент протия представляет собой кольцо. Длина окружности этого кольца равна длине вихревого шнура l(P)

Выразим длину окружности l(P) через диаметр d(P):

l(P) = π d(P).

Откуда определится диаметр титульного химэлемента протия:

d(P) = l(P) / π = 3100 / 3,14 = 987 дш.

8. Длина вихревого шнура химэлемента лития в единицах дш

Титульное количество электронных секций химэлемента лития равно 21100.

Следовательно, длина его вихревого шнура

l(Li) = 21100 дш

9. Диаметр химэлемента лития в единицах дш

Химэлемент лития по форме – почти круглый. Его вихревой шнур свёрнут в 4 одинаковые по размерам петли. Длина шнура одной петли составляет (21100 / 4) = 5275 дш.

Если бы петли имели форму окружности, то их диаметр был бы равен (5275 / 3,14) = 1680 дш.

На самом деле концы петель изогнуты, и их диаметр приближается к диаметру химэлемента протия, тоесть к 987 дш.

Усредним значения и получим диаметр петель = 1300 дш.

Диаметр химэлемента лития равен диаметру петли; следовательно,

d(Li) = 1300 дш.

10. Объём химэлемента лития в единицах дш³

Зная диаметр круглого химэлемента лития, определим его объём по формуле

V(Li) = π d(Li)³/ 6 = π 1300³/ 6 = 1,15*10⁹ дш³

В общей массе химического вещества круглый химэлемент лития занимает несколько больший объём, чем полученный, но меньше объёма куба со стороной 1300 дш:

1,15*10⁹*V(Li)_СР = 2,197*10⁹ дш³.

Примем его равным

V(Li)_СР = 1,5*10⁹ дш³.

11. Объём химэлемента лития в единицах кбм

Плотность инерции химического вещества лития составляет 530 пин. Это означает, что каждый кубометр лития имеет инерцию 530 ин.

Зная инерцию одного химэлемента лития ( I(Li) = 1,15*10^-26 ин), определим количество химэлементов лития в одном кубометре:

.

Разделив кубометр на это количество, получим объём химэлемента лития в единицах кбм:

12. Диаметр эфирного шарика

Приравняем объёмы химэлемента лития в единицах дш³ и кбм:

1,5*10⁹ дш³ = 2,17*10^-29 кбм, -

и определим диаметр эфирного шарика:

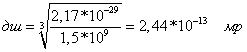
13. Объём эфирного шарика

Зная диаметр эфирного шарика дш, определим его объём V_Ш по формуле

14. Плотность инерции эфирного шарика

Разделив инерцию эфирного шарика i = 1,82*10^-31 ин на его объём V_Ш = 7,60*10^-39 кбм, получим плотность инерции эфирного шарика:

15. Плотность инерции эфира

Очевидно, что искомая плотность инерции эфира ρ будет несколько меньше плотности инерции эфирного шарика ρ_Ш , так как между даже плотно уложенными эфирными шариками остаются пустоты.

Если бы шарики были уложены как кубики, то соотношение объёма шарика (0,5236 д_Ш³) и кубика (д_Ш³) равнялось бы

(0,5236 д_Ш³ / д_Ш³ ) = 0,5236.

Но эфирные шарики уложены более плотно; поэтому это соотношение увеличим до 0,8.

Такую же часть от плотности инерции эфирного шарика ρ_Ш составляет плотность инерции эфира:

ρ = 0,8 ρ_Ш = 0,8*2,39*10⁷ = 1,9*10⁷ пин.

Сравнение. Плотность инерции воды составляет 10³ пин. Следовательно, плотность инерции эфира в

(1,9*10⁷ / 10³) = 1,9*10⁴ = 19000 раз

больше плотности инерции воды.

Плотность инерции эфира – величина непостоянная; она зависит от удельного давления эфира: чем больше давление, тем больше плотность. Однако в пределах ближайшего к нам космоса обе эти величины изменяются очень незначительно.

16. Аналитические зависимости световых волн

Световая волна представляет собой бегущий упругий поперечный прогиб эфирной среды.

Рассмотрим поведение отдельного эфирного шарика, находящегося в зоне световой волны; смотри рисунок.

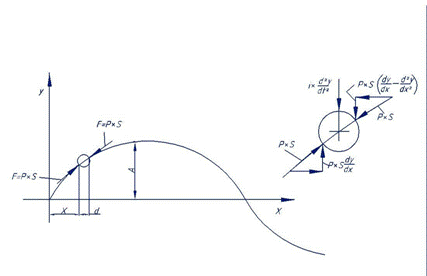
На рисунке прогиб среды (двойная амплитуда А) показан преувеличенным. На самом деле он составляет часть диаметра эфирного шарика.

Также преувеличенным показан сам эфирный шарик по отношению к длине волны. Самая короткая, ультрафиолетовая волна охватывает 12000 шариков, а самая длинная, инфракрасная – охватывает 8,2 миллиарда шариков.

Обозначения:

ось x – направление распространения световой волны;

ось y – поперечное перемещение волны;

d – единичная длина – диаметр эфирного шарика;

S – единичная площадь; S = d²;

A – амплитуда световой волны;

p – удельное давление эфирной среды;

F = p*S – усилие давления среды на эфирный шарик в полосе прогиба;

i – инерция эфирного шарика;

- ускорение эфирного шарика;

- первая производная прогиба – тангенс угла наклона прогиба в координате x;

- вторая производная прогиба;

- тангенс угла наклона прогиба в координате (x + d).

Составим уравнение проекций на ось y усилий, действующих на эфирный шарик:

.

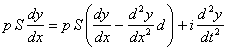После преобразований получим

.

В этой формуле:

- единичный объём;

- плотность инерции эфира.

Окончательный вид формулы:

.

Это – однородное волновое уравнение, подтверждающее, что прогиб эфирной среды носит волновой характер.

В этом уравнении

где c – скорость распространения волны вдоль оси x; в нашем случае – скорость света.

В результате выясняется, что скорость света с имеет следующую зависимость от удельного давления эфирной среды p и плотности инерции эфира ρ :

.

17. Скорость и путь равноускоренного движения

При равноускоренном движении скорость предмета v в каждую секунду увеличивается на постоянную величину; эта величина – ускорение a. Зависимость скорости v от ускорения a и продолжительности движения t следующая:

v = a * t .

Если перед началом ускорения предмет уже имел некоторую скорость v₀ , то последующая скорость v определится как

v = v₀ + a t .

Средняя скорость предмета v_СР при начале движения с нуля будет в два раза меньше:

Путь s, пройденный предметом за продолжительность движения t , равен произведению средней скорости v_СР на эту продолжительность:

S = v_ср t .

В случае начала движения с нуля путь s определится как

Если перед началом ускорения был уже пройден некоторый путь s₀ , то зависимость примет вид

.

Наиболее характерный случай равноускоренного движения – падение тяжёлых предметов с некоторой высоты. Тяжёлые предметы, такие как, например, камни, при падении с большой высоты не испытывают большого сопротивления воздуха, и поэтому в расчётах их движений ускорение можно считать постоянным.

Пример. С отвесной скалы падает камень. Требуется определить скорость падения и путь падения через одну секунду и через 10 секунд.

Ускорение свободного падения определяется земным тяготением и равно 9,8 ускоров.

Через 1 секунду:

v₁ = a t = 9,8 * 1 = 9,8 ск;

.

Через 10 секунд:

v₂ = a t = 9,8 * 10 = 98 ск ;

.

18. Энергия движения предмета

Энергия движения по определению выражается в том количестве движений, которое вкладывается в перемещение на расстояние s с постоянным усилием F. Это отображается следующей зависимостью:

E = F*s.

Приложим усилие F к предмету с инерцией I ; предмет получит ускорение a. связь между этими величинами – следующая:

F = I*a.

Скорость предмета будет изменяться по закону

V = a*t,

где t – продолжительность ускорения.

Извлечём из этой формулы ускорение a:

Подставим это ускорение в выражение для усилия F:

Средняя скорость движения предмета определяется как

Выразим через эту среднюю скорость пройденный путь:

Подставим полученные зависимости усилия F и пути s в выражение для энергии движений E и получим

Энергия любого движущегося предмета равна произведению его инерции на половину квадрата его скорости.

Пример. Вычислим энергию, какую сообщит земле камень, падающий на неё с высоты h = 100 метров; инерция камня I = 10 ин.

Сначала определим конечную скорость камня. Мы знаем, что скорость при свободном падении изменяется по следующему закону:

V = a t = 9,8 t .

Продолжительность падения определим из формулы пути

:

.

Численное значение конечной скорости падения:

V = 9,8 t = 9,8 * 4,5 = 44,3 ск.

Получив скорость, определим энергию камня:

Такую энергию сообщит камень земле.

19. Энергия фотона

Из однородного волнового уравнения

следует синусоидальный незатухающий характер световой волны.

Примем за начало отсчёта времени такой момент, когда поперечное отклонение эфирных шариков светонесущей эфирной среды описывается следующим выражением:

y = A cos ωt,

где A – амплитуда световой волны; ω – круговая частота волны в рад/с; t – текущее время.

Фотон представляет собой один период световой волны.

По ширине фотон охватывает n эфирных шариков.

В основу определения энергии фотона положим зависимость

Так как на всей длине фотона скорости поперечного отклонения его шариков разные, то общая энергия фотона будет складываться из энергий отдельных его шариков.

Упростим представление фотона и будем считать его сплошной лентой.

Поперечная скорость любой точки этой ленты определится как первая производная от отклонения (находим из справочника по математике):

.

Выделим из всего периода колебаний световой волны малый участок времени продолжительностью Δt.

Плотность энергии на этом участке определится как

.

Позиция времени t соответствует середине участка. При малых значениях Δt скорость поперечного отклонения шариков считаем постоянной.

Выражение характеризует плотность инерции по времени на данном участке.

Чтобы определить энергию всего фотона, нужно проинтегрировать плотность энергии по времени в пределах фотона.

В дифференциальной форме энергия фотона будет иметь вид

.

Интегрирование – в пределах одного периода: t₁ = 0; t₂ = T = 2π /ω.

Так как на протяжении целого периода эфирные шарики отклоняются сначала, в первой половине периода – в одну сторону, а потом, во второй половине – в противоположную, то энергии полупериодов будут вычитаться друг из друга и в результате дадут ноль.

Поэтому необходимо провести интегрирование только в пределах полупериода, а полную энергию фотона определять как удвоенную энергию полупериода. Пределами интегрирования в таком случае будут: t₁ = 0; t₂ = T / 2 = π / ω :

.

Постоянные величины A² и ω² вынесем за пределы интеграла:

.

Плотность инерции по времени на всей длине фотона и на всей длине световой волны сохраняется постоянной; её определяет цепочка эфирных шариков шириной в n шариков. В общем виде плотность инерции по времени отражает участие инерции в единицу времени, тоесть в секунду. За секунду световая волна пробегает путь, численно равный скорости света c . На этой длине укладывается m эфирных шариков диаметром d; их плотность во времени при ширине в n шариков составит

В результате плотность инерции во времени можно определить как произведение плотности шариков на их инерции I :

Из справочника по математике находим:

Применительно к нашему случаю:

.

Нижний предел интегрирования t₁ = 0:

Верхний предел интегрирования t₂ = π / ω :

.

Разность составит:

.

После подстановки всех полученных величин в формулу для энергии фотона получим

Радианную частоту колебаний ω можно заменить частотой f в колебанах по соотношению ω = 2π f и получим:

Ещё раз раскроем обозначения:

i – инерция эфирного шарика; n – ширина фотона в шариках; c – скорость света; A – амплитуда фотона; f – частота колебаний в колебанах; d – диаметр эфирного шарика.

20. Размерности должны сходиться

В теоретических физических законах прямого действия размерности должны сходиться; это – закон законов. Если размерности не сходятся и вводится согласующий коэффициент, то данный теоретический закон либо недоработан, либо вообще ошибочен.

Проверим на сходимость размерностей полученные выражения.

1. Скорость света:

.

Представим её последовательно в размерностях:

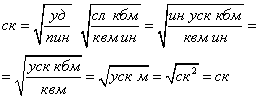
Размерности сходятся.

2. Энергия движений фотона:

.

В этой формуле (i n) отражает суммарную инерцию, а диаметр эфирного шарика в выражении (c/d) представлен как путь, проходимый со скоростью света c.

Размерности энергии движений фотона:

.

Размерности сходятся.

21. Амплитуда световой волны

Представим энергию фотона как

E = h ω,

где

Отсюда определим выражение для амплитуды A:

.

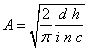Из экспериментальной физики известно, что для фотона с наиболее распространённой шириной величина h = 1,055*10^-34 дж *с.

Ширина фотона может быть разной: от 3 до 1000 и более эфирных шариков. Будем считать, что наиболее распространённой шириной фотона видимого диапазона является n = 500.

Прочие численные значения величин:

i = 1,82*10^-31 ин;

d = 2,44*10^-13 мр;

с = 3*10⁸ ск.

Подставим численные значения величин в формулу для амплитуды A и получим

.

Амплитуда световой волны видимого диапазона оказывается в 10 раз меньше диаметра эфирного шарика.

22. Ускорение эфирных шариков при срыве световой волны

Из однородного волнового уравнения следует, что в синусной форме ускорение эфирных шариков в фотоне определяется выражением

.

Будем считать, что срыв световой волны происходит при максимальном ускорении:

a = A ω².

Средняя частота колебаний в видимом диапазоне f = 6,0*10¹⁴ кб. Переведём её в круговую частоту:

ω = 2π f = 3,8*10¹⁵ рад/с.

Амплитуда A = 0,25*10^-13 мр.

Подставим данные величины в формулу ускорения и получим

a = 0,25*10^-13 *(3,8*10¹⁵)² = 3,6*10¹⁷ уск.

Только при достижении такого значения ускорения эфирных шариков происходит срыв световой волны. Это значит, что центральная часть колеблющейся струны химэлемента отклоняется с таким же ускорением. При меньших значениях ускорений струны её колебания порождают лишь тепловые волны. Эти волны «привязаны» к источнику и в пространство не уходят.

23. Удельное давление эфира

Из формулы для скорости света

извлечём удельное давление эфира p:

p = ρ c².

Скорость света c = 3*10⁸ ск. Плотность инерции эфира определена ранее: ρ = 1,9*10⁷ пин.

Подставляя в формулу для определения удельного давления эфира p, получим:

p = 1,9*10⁷*(3*10⁸)² = 1,70*10²⁴ уд.

Эта величина настолько велика, что её не с чем сравнивать.

Удельное давление эфира – величина непостоянная. По мере приближения к планетам и звёздам (в зонах их тяготения), удельное давление эфира уменьшается, но очень незначительно. Уменьшается оно и при приближении к вихревым шнурам химэлементов; там это уменьшение – очень существенное.

24. Численное значение энергии фотона

Аналитическая зависимость энергии фотона имеет следующий вид:

Численные значения входящих в выражение величин:

i = 1,82*10^-31 ин;

n = 500;

c = 3*10⁸ уск;

A = 0,25*10^-13 мр;

f = 6*10¹⁴ кб;

d = 2,44*10^-13 мр.

При этих значениях величин энергия фотона оказывается равной

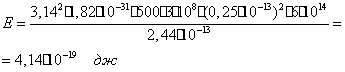
25. Объём пустоты фотона

Движения эфирных шариков фотона порождают пустоту. При этом колеблющиеся шарики преодолевают давление эфирной среды.

Зависимость объёма пустоты g от энергии движений фотона E и удельного давления эфирной среды p следующая:

Удельное давление эфира нами определено: p = 1,7*10²⁴ уд.

Энергию фотона принимаем такой, какая получена в предыдущем расчёте при выбранных параметрах n, A, f : E = 4,14*10^-19 дж.

Подставим численные значения параметров в формулу g и получим:

Пустота фотона важна в том смысле, что помогает объяснить такие световые явления, как преломление лучей, рассеивание солнечного света, огибание кромок и кажущееся уменьшение скорости света в оптических средах.

Во всех этих явлениях срабатывает закон вытеснения пустоты. Согласно этому закону пустота вытесняется в сторону меньшего удельного давления среды.

И хотя пустота фотона ничтожно мала, в зонах тяготения с крутым уклоном удельного эфирного давления она вызывает искривление траектории его распространения.

Проходя, например, вблизи звёзд, луч света искривляется, и это зафиксировано астрономами.

Несравнимо большее искривление траектории фотона вызывает уклон пришнурового удельного эфирного давления.

26. Уклон удельного эфирного давления в пришнуровой зоне химэлемента

Проходя вблизи вихревых шнуров химэлементов, фотон сворачивает в их сторону довольно значительно, и каждый из нас фиксировал это.

Так при входе под углом в воду фотон огибает первые попавшиеся на его пути химэлементы и уходит в неё более круто; возникает видимое преломление лучей.

При выходе из воды наблюдается то же самое явление – луч отклоняется в сторону воды.

В самой воде, как и в любом прозрачном материале, фотон огибает все встречающиеся на его пути химэлементы и в равной степени отклоняется в разные стороны. В результате общее направление его движения сохраняется, но траектория его движения становится волнообразной. Двигаясь по такой траектории, фотон вынужден пробегать лишнее расстояние. Возникает впечатление, что его скорость в воде как-будто уменьшается.

Огибание светом химэлементов происходит и в облаках. Оно приводит к тому, что параллельные солнечные лучи отклоняются в разные стороны и создают рассеянный свет.

Рассмотрим уклон удельного эфирного давления в пришнуровой зоне химэлемента.

Внутри вихревого шнура удельное давление равно нулю. По мере удаления от шнура оно растёт и на относительно большом удалении достигает своего максимума – удельного давления среды.

Уменьшение удельного давления в пришнуровой зоне вызывают колебания шариков в этой зоне. Эти колебания – следствие соударения примыкающих шариков среды с шариками вихря. Они (колебания) происходят в плоскостях электронных секций и направлены касательно к оболочке шнура.

Проще всего допустить, что удельное эфирное давление в пришнуровой зоне изменяется по экспоненте:

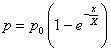
где p₀ = 1,7*10²⁴ уд – удельное эфирное давление окружающей среды; x – удалённость от оси вихревого шнура; X – катет начального уклона.

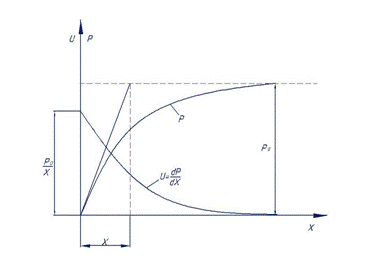
Для того, чтобы получить выражение для определения уклона удельного эфирного давления, необходимо продифференцировать экспоненту. Приведём сначала её к виду

.

Воспользовавшись справочником по математике, находим выражение для уклона пришнурового удельного давления:

.

Начальный уклон формируется на вихревой оболочке и на прилегающих к ней эфирных шариках, так что катет начального уклона можно принять равным X =(3… 5) дш .

С учётом этого выражение для уклона примет вид

.

В этом выражении удалённость x задана также в единицах дш.

27. Энергия распада химэлементов

Распад химэлементов бывает неполным и полным.

Неполный распад это – отрывы от вихревого шнура химэлемента кусков, обрывков, таких как нейтроны, альфа-частицы и других.

При полном распаде оторванные обрывки распадаются до электронов. Это означает, что электронные секции обрывков раздавливаются и их эфирные шарики рассеиваются, теряя свои вихревые движения. Шарики возвращаются в эфирную среду.

В обоих видах распада уменьшается объём внутривихревой пустоты, только в случае неполного распада объём этот – небольшой, а при полном распаде – максимально возможный.

Сохраняется пустота только у электронов, но её доля в общем объёме – ничтожная.

Пустота при распаде захлопывается эфирным давлением. Движения захлопывания превращаются в тепловые движения оставшихся химэлементов. Получается так, что химэлемент своим распадом согревает соседей.

Исчезнувшая пустота уменьшает вес распадающегося химического вещества. Тяготение к земле определяется пустотой: она вытесняется эфирным давлением под уклон, тоесть в сторону земли. Нету пустоты – нет и тяготения.

Итак, распад химэлементов порождает теплоту и уменьшает вес.

Зная это, можно экспериментально определить их соотношение.

В физике обычно оперируют не весом, а инерцией; они эквивалентны. Так что определялось соотношение выделенной теплоты и уменьшения инерции.

Предполагалось, что в пересчёте на один ин инерции полностью распавшегося химического вещества должно было выделяться 9*10¹⁶ движей тепловой энергии.

Однако эксперименты показали, что выделялось приблизительно в два раза меньше теплоты.

Таким образом, теплотворная способность распада оценивается в 4,5*10¹⁶ дж/ин.

Для сравнения, удельная теплота сгорания бензина составляет всего 4,5*10⁷ дж/ин, тоесть в миллиард раз меньше.

Эксперименты показали также, что соотношение выделенной энергии и потерянной инерции у всех распадающихся химических веществ одинаковое.

Обозначим указанное соотношение буквой q и примем его равным

q = 4,5*10¹⁶ дж/ин.

28. Внутренняя энергия предмета

Внешняя энергия предмета выражается в его видимых движениях; например – движущийся автомобиль.

Внутренняя энергия предмета определяется энергией вихревых движений всех его химэлементов.

Зная, что при полном распаде химэлементов выделяется q движей энергии на каждый потерянный ин инерции, приходим к выводу, что до распада было такое же соотношение и такое же соотношение – у всех прочих химических веществ. Это следует из закона сохранения движений.

Внутренняя энергия любого предмета E определится, таким образом, как

E = q*I = 4,5*10¹⁶ I , дж,

где I – инерция предмета.

Внутренняя энергия есть не только у твёрдых предметов, но и у жидкостей и газов; она есть у всех химических веществ.

Внутреннюю энергию иногда в физике называют энергией покоя.

29. Пустота эквивалентна энергии

Пустота эквивалентна энергии – это закон Природы.

Этот закон распространяется и на эфирную среду. Всякие движения в ней порождают пустоту, и пустота там – абсолютная.

Шнур химэлемента представляет собой вихрь. Внутри этого вихря – пустота. Объём этой пустоты эквивалентен энергии вихря. Энергия вихря уходит на то, чтобы раздвинуть эфирную среду, а она - очень сильно сдавлена: удельное давление эфира составляет p = 1,7*10²⁴ уд.

В общем случае объём пустоты g в эфире пропорционален энергии движений E: чем больше энергия, тем больше объём,- и обратно пропорционален удельному давлению эфира p: чем больше давление, тем меньше объём.

Зависимость эта имеет следующий вид:

Подставим в эту зависимость численное значение p и получим

Таково соотношение энергии движений и объёма пустоты в эфире.

30. Эквивалент инерции и внутренней пустоты предмета

Для того, чтобы определить объём внутренней пустоты предмета, необходимо в зависимость

g = 5,88*10^-25 E

подставить значение внутренней энергии предмета E = 4,5*10¹⁶*I . После подстановки получим:

g = 5,88*10^-25*4,5*10¹⁶ I = 2,65*10^-8 I , кбм/ин.

Как видим, объём внутренней пустоты предмета определяется его инерцией: в каждом инее инерции содержится 2,65*10^-8 кубометра абсолютной пустоты. Если перевести кубометры в кубические сантиметры, то в каждом ине – 0,0265 см³ пустоты.

Точно такое же соотношение и в жидкостях, и в газах.

В кубометре воды – 1000 ин; следовательно, в кубометре воды (0,0265*1000) = 26,5 кубических сантиметров пустоты.

Отношение внутренней пустоты g предмета к его инерции I :

, -

изменяется в зависимости от удельного давления эфира, но это изменение в реальности столь незначительное, что такое отношение можно считать эквивалентом инерции и внутренней пустоты предметов.

31. Объём внутренней пустоты химэлементов

Химические вещества состоят из химэлементов; поэтому на химэлементы распространяется то же соотношение пустоты и инерции.

Определим объёмы внутренней пустоты некоторых химэлементов.

Протий P.

Инерция: I = 1,69*10^-27 ин.

Объём пустоты:

g = 2,65*10^-8*1,69*10^-27 = 4,48*10^-35 кбм.

Литий Li.

Инерция: I = 1,15*10^-26 ин.

Объём пустоты:

g = 2,65*10^-8*1,15*10^-26 = 3,05*10^-34 кбм.

Углерод C.

Инерция: I = 1,99*10^-26 ин.

Объём пустоты:

g = 2,65*10^-8*1,99*10^-26 = 5,27*10^-34 кбм.

Внутренняя пустота химэлементов говорит не только о внутренней энергии, но и о том, что в зоне тяготения с уклоном удельного эфирного давления она (пустота) вытесняется в сторону меньшего давления эфирной среды. Благодаря этому химэлементы слипаются между собой и образуют твёрдые материалы; благодаря этому химические вещества тяготеют к земле.

32. Объём внутренней пустоты электронной секции химэлемента

Вихревые шнуры химэлементов состоят из электронных секций, и поэтому соотношение пустоты и инерции в равной степени распространяется и на электронные секции.

Электронная секция состоит из трёх эфирных шариков; инерция эфирного шарика = 1,82*10^-31 ин; инерция самой секции = 1,82*10^-31*3 = 5,46*10^-31 ин.

Объём внутренней пустоты электронной секции:

g = 2,65*10^-8*5,46*10^-31 = 1,45*10^-38 кбм.

Представим объём внутренней пустоты электронной секции в объёмах эфирных шариков.

Сначала определим объём отдельного эфирного шарика:

.

Разделим объём внутренней пустоты секции в кубометрах на объём эфирного шарика в тех же кубометрах и получим объём пустоты электронной секции в эфирных шариках (эш):

.

33. Объём шариковой оболочки электронной секции

Оболочка электронной секции состоит из трёх эфирных шариков.

Оболочка секции занимает такой объём, какой занимали бы три эфирных шарика при вращении с малой скоростью, когда внутренняя пустота секции равнялась бы практически нулю. В сечении такая секция выглядела бы как три сомкнувшихся эфирных шарика.

Объём оболочки электронной секции можно представить как произведение площади круга диаметром D₁ на длину секции.

Диаметр D₁ определим геометрически:

.

Площадь круга диаметром D₁ :

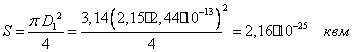
Длина электронной секции равна диаметру эфирного шарика:

l = d = 2,44*10^-13 м.

Объём оболочки электронной секции определится как

V = S l = 2,16*10^-25*2,44*10^-13 = 5,27*10^-38 кбм.

Представим этот объём в объёмах эфирных шариков

.

34. Отношение объёма внутренней пустоты к объёму оболочки электронной секции

Это отношение определится как

35. Объём электронной секции

Объём электронной секции складывается из объёма её оболочки и объёма внутренней пустоты:

V = 5,27*10^-38 + 1,45*10^-38 = 6,72*10^-38 кбм.

Тот же объём – в эфирных шариках:

V = 6,94 + 1,91 = 8,85 эш.

Отношение объёма внутренней пустоты к объёму всей секции:

36. Наружный диаметр вихревого шнура химэлемента

Представим объём электронной секции как произведение площади её сечения на её длину, тоесть на диаметр эфирного шарика:

V = S d.

Отсюда площадь сечения вихревого шнура определится как

Площадь сечения, в свою очередь, можно выразить через диаметр вихревого шнура:

Искомый диаметр вихревого шнура будет равен:

.

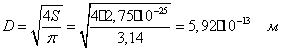Он больше диаметра эфирного шарика в

(5,92*10^-13 / 2,44*10^-13) = 2,43 раза.

Сечение вихревого шнура не является идеальным кругом. Эфирные шарики шнура не просто бегают по окружности – они прыгают по таким же, как они, шарикам эфирной среды. Поэтому вычисленный диаметр вихревого шнура следует воспринимать как усреднённый диаметр.

37. Внутренний диаметр вихревого шнура химэлемента

Внутренний диаметр вихревого шнура меньше его наружнего диаметра на два диаметра эфирного шарика:

d = 5,92*10^-13 – 2*2,44*10^-13 = 1,04*10^-13 м.

Определим – какую часть диаметра эфирного шарика составляет внутренний диаметр вихревого шнура:

1,04*10^-13 / 2,44*10^-13 = 0,43.

38. Осевые усилия вихревых обрывков

Торцы вихревых обрывков заткнуты эфирными шариками. Эфирное давление прижимает торцовые шарики к крайним электронным секциям вихревых обрывков с усилием

F = p d²,

где p = 1,70*10²⁴ уд – удельное эфирное давление; d = 2,44*10^-13 м – диаметр эфирного шарика.

В данном выражении вместо круга (π d² / 4) принят квадрат d², так как удельное давление рассчитывается без учёта пустот между эфирными шариками.

В числах:

F = p d² = 1,70*10²⁴*2,44²*10^-26 = 0,10 сл.

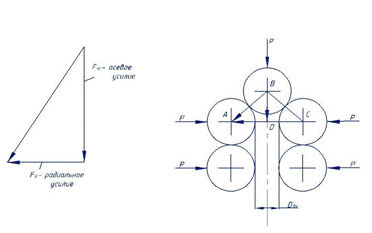
Осевое усилие F воздействует на 3 эфирных шарика крайней электронной секции. На каждый из этих шариков в отдельности приходится усилие F_ОС :

F_ОС = F / 3 = 0,10 / 3 = 0,0337 сл.

39. Усилие радиального раздавливания вихревого обрывка

Торцовый шарик создаёт радиальное усилие раздавливания F_Р на каждый шарик крайней электронной секции.

Для определения этого усилия воспользуемся геометрическим соотношением

.

Отсюда:

.

Определим размеры катетов AD и BD:

,

где D_ВН = 1,04*10^-13 мр – внутренний диаметр вихревого шнура; d = 2,44*10^-13 – диаметр эфирного шарика; в числах:

Катет BD определим из прямоугольного треугольника ABD:

BD² = AB² – AD²;

.

Гипотенуза AB = d = 2,44*10^-13 м.

Катет

.

Численное значение BD:

В результате усилие радиального раздавливания вихревого обрывка, приходящееся на один шарик электронной секции, определится как

.

Как видно, радиальное усилие раздавливания (0,0343 сл) соизмеримо с усилием, создаваемым удельным эфирным давлением, действующим на тот же шарик (0,10 сл). А с учётом того, что шарик электронной секции испытывает дополнительное радиальное инерционное сопротивление от вращения, крайняя электронная секция вихревого обрывка находится в хрупком равновесии, и любой удар по торцовому шарику способен вызвать раздавливание секции.

40. Инерция поворота – аналитическая зависимость

Поступательно движущийся предмет характеризуется инерцией I . Инерция определяет поступательное ускорение a в зависимости от усилия F, приложенного к данному предмету:

Вращающийся предмет характеризуется инерцией поворота I_O.Она определяет также ускорение поворота ε в зависимости от усилия поворота M:

.

А чему равна сама инерция поворота предмета I_O ?

Произведём следующие преобразования. Выразим усилие F через инерцию I и ускорение a :

F = I a .

Умножим и разделим правую часть выражения на радиус r:

Отношение (a / r) является угловым ускорением поворота ε.

Умножим обе части выражения снова на радиус r:

F r = I r² ε.

Получим:

F r = M – усилие поворота;

I r² = I_O – инерция поворота.

Инерция поворота предмета определяется как сумма инерций поворота его частей.

41. Инерция поворота электронной секции химэлемента

Сначала произведём упрощенный расчёт. Будем считать, что вся инерция эфирных шариков секции сосредоточена в центрах этих шариков. Расстояние от оси вращения до центров шариков составляет половину внутреннего диаметра секции плюс половина диаметра эфирного шарика:

Инерция поворота электронной секции при упрощённом расчёте определится как утроенная инерция поворота отдельного шарика:

I_O = 3 I r² = 3*1,82*10^-31*(1,74*10^-13)² = 1,65*10^-56 инп.

Для точного расчёта предлагается выражение без его вывода:

,

где ρ_Ш – плотность инерции эфирного шарика.

После подстановки в выражение d_ВН = 1,04*10^-13 м , d = 2,44*10^-13 , ρ_Ш = 2,39*10⁷ получим численное значение инерции поворота электронной секции:

I_O = 1,81*10^-56 инп.

Погрешность ранее выполненного упрощенного расчёта составляет

.

42. Внутренняя энергия электронной секции химэлемента

Она определяется как произведение удельного эфирного давления p на объём внутренней пустоты g :

E = p g = 1,7*10²⁴*1,45*10^-38 = 2,47*10^-14 дж.

43. Энергия вращения предмета

Энергия вращения предмета по определению:

E = M φ,

где M – усилие поворота; φ – угол поворота.

Выразим усилие поворота M через инерцию поворота предмета I_O и его ускорение поворота ε:

M = I_O ε.

При постоянном усилии поворота ускорение поворота будет также постоянным; такое вращение называется равноускоренным.

Скорость вращения ω и угол поворота φ в таком случае имеют следующие зависимости:

,

где t – продолжительность равноускоренного вращения.

Из ω = ε t определим ε:

.

Подставим эти выражения в основные формулы:

;

.

Энергия вращения предмета равна произведению инерции поворота предмета на половину квадрата его скорости вращения.

Скорость вращения ω задаётся в радианах в секунду – рад/с.

Пример. Определим энергию вращения велосипедного колеса при движении велосипеда со скоростью v = 15 км/час. Инерция колеса I = 2 ин; диаметр колеса d = 0,6 м.

Сначала определим инерцию поворота I_O велосипедного колеса. Считаем, что вся инерция сосредоточена в ободе и в шине колеса. Радиус колеса r = 0,6 / 2 = 0,3 м. Инерцию поворота вычисляем по формуле

I_O = I r² = 2*0,3² = 0,18 ин*м².

Длина окружности колеса:

l = π d = 3,14*0,6 = 1,88 м.

Скорость велосипеда пересчитаем в м/с:

V = 15 км/час = 15000 м/час = 250 м/мин = 4,17 м/с.

Частота вращения колеса:

Скорость вращения в единицах рад/с:

ω = 2 π f = 2*3,14*2,22 = 13,94 рад/с.

Энергия вращения велосипедного колеса:

.

44. Скорость вращения вихря химэлемента

Скорость вращения вихря является в то же время скоростью вращения отдельной электронной секции; её и будем определять.

Из зависимости

определим скорость вращения ω:

,

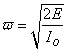где E – внутренняя энергия электронной секции; I_O – инерция поворота электронной секции.

В свою очередь внутреннюю энергию секции можно выразить через объём её внутренней пустоты g и давление эфира p:

E = p g .

Подставляя это выражение в формулу скорости вращения, получим:

.

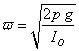Как видно, скорость вращения вихря химэлемента зависит от давления эфира: чем больше давление, тем выше скорость вращения. Давление эфира в нормальных условиях изменяется незначительно; также незначительно изменяется скорость вращения.

Определим численное значение скорости вращения вихря химэлемента; для этого в её выражение подставим следующие величины: E = 2,47*10^-14 дж – внутренняя энергия электронной секции; I_O = 1,81*10^-56 инп – инерция поворота секции.

В результате получим

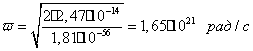
Переведём радианную скорость вращения ω в частоту вращения f:

.

С такой же скоростью вращается электрон.

45. Продолжительность одного оборота вихревого шнура химэлемента

Продолжительность одного оборота вихревого шнура t₀ обратна частоте вращения f :

.

Так как это событие (один оборот вихревого шнура) лежит в основе всех прочих событий, происходящих в Природе, то его можно принимать как элементарное событие.

Это элементарное событие определяет ход времени.

46. Объём внутренней пустоты электрона

Торцовые шарики электрона уменьшают объём внутренней пустоты электронной секции ровно на один шарик. И если у электронной секции объём пустоты составляет 1,91 эфирных шарика, то у электрона он равен

(1,91 – 1) = 0,91 эш.

Объём одного эфирного шарика в единицах кбм составляет 7,60*10^-39 кбм; следовательно, объём внутренней пустоты электрона равен

(7,60*10^-39*0,91) = 6,90*10^-39 кбм.

47. Тяготение электрона

Все мы наблюдали, как молнии бьют в землю. На основании этого можно подумать, что электроны тяготеют к земле также, как обычные химические вещества.

На самом деле электроны тяготеют значительно слабее.

Ещё раз напомним, что усилие тяготения предмета определяется объёмом его внутренней пустоты.

Сравним тяготение электронной секции и электрона с учётом их инерций.

Инерция любого предмета определяется суммарной инерцией эфирных шариков, составляющих этот предмет.

У электронной секции объём пустоты составляет 1,91 эш, а сама секция состоит из трёх эш. Отношение объёма пустоты к числу эфирных шариков у секции

(1,91 / 3) = 0,637.

У электрона объём пустоты на один эш меньше: (1,91 – 1) = 0,91 эш, а состоит электрон из пяти эш. Отношение объёма пустоты к числу эфирных шариков у него

(0,91 / 5) = 0,182.

Получается так, что электрон тяготеет в

(0,637 / 0,182) = 3,5 раза

слабее, чем электронная секция, тоесть в 3,5 раза слабее химэлементов.

И когда мы видим молнию, ударяющую в землю, мы должны понимать, что электроны молнии гонит к земле не столько земное тяготение, сколько перепад удельных электронных давлений.

48. Инерционное сопротивление при движении предмета по кривой траектории

Для того, чтобы заставить предмет свернуть, нужно приложить к нему боковое усилие.

Инерция предмета будет оказывать при этом сопротивление.

Инерционное сопротивление сказывается при любом искривлении траектории. Наиболее характерным случаем является движение по окружности, тоесть обычное вращение.

Выясним аналитическую зависимость инерционного сопротивления.

Любая кривая траектория характеризуется радиусом кривизны r.

Будем считать, что скорость предмета по траектории v постоянная.

В этом случае поворачивающее усилие F будет направлено по радиусу к центру поворота. И по этому же радиусу, но наружу, будет действовать инерционное сопротивление R. И только в этом случае они равны между собой:

R = F.

Рассмотрим малый промежуток времени Δt .

За это время предмет переместится из положения A в положение B. Длина дуги AB определится как произведение скорости v на продолжительность Δt:

AB = v* Δt.

За это же время предмет приобретёт поперечную скорость Δv.

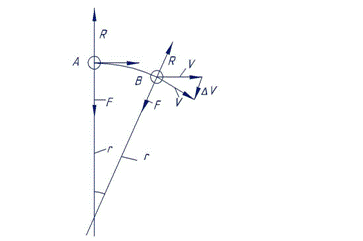
Далее рассмотрим подобие треугольников, считая, что дуга AB равна хорде AB. При малых смещениях погрешность будет незначительной, а при переходе к дифференциальной форме она исчезает совсем – остаётся только качество изменения.

Радиус r относится к хорде AB также, как скорость по траектории v относится к поперечной скорости Δv ^

Подставим сюда значение AB :

Извлечём из этого равенства отношение поперечной скорости Δv к продолжительности Δt :

При переходе к дифференциальной форме отношение превращается в ускорение a :

Это ускорение создаётся поворачивающим усилием F:

где I – инерция предмета.

Отсюда:

Так как поворачивающее усилие F определяется инерционным сопротивлением R и равно ему (направления их действий не учитываем), то в результате получим:

В случае вращения окружную скорость v можно заменить угловой скоростью ω из соотношения v = ω r :

R = I ω² r.

Инерционное сопротивление при вращении иногда называют «центробежным» усилием.

Пример. Чтобы иметь численное представление об инерционном сопротивлении при движении по кривой траектории, рассмотрим крутой вираж автомобиля. Допустим, автомобиль входит в крутой поворот радиусом r = 30 м с недопустимо большой для такого случая скоростью 60 км/час. Разделим скорость на 3600 секунд и получим секундную скорость v = 17 м/с.

Инерция автомобиля I = 1000 ин.

Далее считаем по формуле:

Такое сопротивление повороту будет испытывать автомобиль; в переводе на килограммы это сопротивление равно тонне. Бокового трения шин по асфальту едва ли хватит для того, чтобы удержать автомобиль на дороге.

Инерционное сопротивление испытывают не только автомобили на повороте, но и все вращающиеся предметы и все предметы, движущиеся по кривым траекториям. Испытывают инерционное сопротивление и спутники Земли и сама Земля при движении вокруг Солнца.

49. Тяготение планет

Впечатление – будто Земля притягивает и поэтому все предметы падают вниз – ложное. В Природе притяжения нет.

В действительности все предметы к земле стягивает эфир, и даже не стягивает, а выталкивает их.

Тяготение Земли определяется законом вытеснения пустоты. Закон гласит: пустота вытесняется в сторону меньшего удельного давления среды.

Чем выше над землёй, тем удельное давление эфира больше; уклон направлен в сторону земли. И все предметы «скатываются» под этот уклон.

У закона вытеснения – две составляющие: 1) пространство с переменным удельным давлением среды (в данном случае – эфира) и 2) предметы, наполненные пустотой.

О пустоте мы уже говорили. Она заключена в химэлементах, из которых состоят предметы.

Мы выяснили, что объём пустоты предмета эквивалентен его инерции: чем больше инерция, тем больше пустоты. Соотношение такое: каждый ин инерции предмета содержит 2,65*10^-8 кубометра пустоты.

Теперь попытаемся разобраться с пространством тяготения вокруг Земли. Впрочем, оно по характеру такое же, как и вокруг любой планеты и вокруг любой звезды.

Вихревые движения химэлементов удерживают пустоту, и поэтому планеты и звёзды насыщены ею. Вихревые движения – стационарные.

Но есть ещё нестационарные движения, например световые волны. Уходя прочь от планеты или звезды, они оставляют после себя разрежение эфирной среды, которое ничем не удерживается и которое компенсируется притоком из космоса эфира. Можно сказать даже так: откуда уходят движения, туда устремляется эфир. Именно этот поток создаёт то переменное удельное давление эфира, которое определяет тяготение.

Основной и, пожалуй, единственной причиной появления нестационарных движений в эфире и, следовательно, пространств тяготении является распад химэлементов.

Объём высвобождаемой при распаде пустоты V связан с энергией распада E следующей зависимостью:

где p –удельное давление эфира.

Напомним, что на поверхности Земли удельное давление эфира p = 1,7*10²⁴ уд.

В результате распада химэлементов возникает центростремительный поток эфира Q; он характеризуется следующей зависимостью:

где t – продолжительность.

В этом потоке по ходу его удельное давление эфира падает. Чем дальше от планеты, тем удельное давление эфира больше; чем ближе – тем меньше. Возникает уклон удельного эфирного давления u.

Все предметы и все химические вещества вытесняются под этот уклон. Такое явление мы называем тяготением планет и звёзд.

50. Эфировороты

Любой центростремительный поток текучей среды срывается в плоский вихрь, в котором частицы движутся по спирали, сходящейся к центру; это – закон Природы.

Началом возникновения плоского вихря может быть любое случайное отклонение частиц центростремительного потока от строго радиального направления. Появляется окружная скорость. Двигающиеся по огибающим центр траекториям частицы испытывают инерционное сопротивление своему повороту и стремятся уйти от центра, но усилия, создаваемые перепадом удельных давлений, гонят их к центру. Появляется спиральная траектория движения частиц.

Так возникают водовороты.

Также возникают эфировороты.

Над полюсами планет (или звезды) эфир спускается по винтовой линии вокруг оси вращения. Направление вращения – с запада на восток.

По мере удаления от полюса в сторону средних широт винтовая линия расходится в винтовую спираль.

При приближении к экватору винтовая спираль эфирного потока сжимается в осевом направлении и в экваториальной плоскости превращается в плоскую спираль, сходящуюся к планете.

На экваторе северная и южная плоские спирали эфирных потоков смыкаются между собой.

Если взглянуть на эфироворот со стороны, то он представляет собой вращающийся диск с утолщением в центре.

Диаметр диска зависит от центростремительного потока, который, в свою очередь, зависит от интенсивности распада химэлементов внутри планеты или звезды. В результате чем интенсивнее распад, тем больше диаметр эфироворота.

У Солнца, например, эфироворот распространяется на расстояние от него не менее чем на 6 миллиардов километров (6*10¹² м). Самая дальняя планета Солнечной системы – Плутон удалена от Солнца на 5,91 миллиарда километров и устойчиво удерживается в зоне влияния Солнечного эфироворота.

Эфировороты всех планет Солнечной системы располагаются внутри Солнечного эфироворота и поэтому имеют чёткие границы. Эфироворот Луны располагается внутри эфироворота Земли и поэтому также имеет чёткие границы.

Чёткость границ объясняется тем, что захваченный эфироворотами эфир может двигаться по траекториям какого-то одного потока. Эфир Лунного эфироворота движется по своим траекториям, а эфир Земного – по своим.

Наибольшая толщина дисков эфироворотов – в центрах. Чем дальше от центров, тем толщина – меньше.

Любой предмет испытывает тяготение планеты или звезды только в пределах их эфироворотов. За пределами эфироворотов тяготение планет и звёзд не сказывается.

51. Усилие тяготения в эфироворотах

Усилия тяготения предметов в эфироворотах создают не сами центростремительные потоки эфира в них, а уклоны удельных эфирных давлений, создаваемые ими.

Эти усилия подчиняются закону вытеснения пустоты, который в равной степени распространяется и на эфировороты. Согласно этому закону усилие вытеснения предмета определяется выражением

F = u g ,

где u – уклон удельного эфирного давления в точке расположения предмета; g – объём внутренней пустоты предмета.

Объём внутренней пустоты g связан с инерцией предмета I эквивалентом e :

Отсюда:

g = e I .

Подставим эту зависимость в формулу усилия тяготения и получим

F = u g = e u I .

Численное значение эквивалента: e = 2,65*10^-8 мр²мп/ин. С учётом этого усилие тяготения предмета с инерцией I в точке эфироворота с уклоном u определится как

F = 2,65*10^-8 u I.

52. Экспериментальная закономерность тяготения предметов в эфироворотах

Экспериментально установлено, что усилие тяготения предмета F в эфировороте пропорционально инерции предмета I и обратно пропорционально квадрату расстояния его от центра эфироворота r :

Величина A является согласующим коэффициентом тяготения. Этот коэффициент определяется интенсивностью распада химэлементов внутри планет и звёзд.

У каждого космического объекта (планеты или звезды) – свой коэффициент тяготения.

Величина коэффициента у каждой планеты (звезды) – более-менее стабильна; по крайней мере, отклонения от среднего значения столь незначительные, что на практике они не обнаруживаются.

Выясним размерность коэффициента тяготения. Его зависимость такая:

Размерность усилия F : .

Размерность (I / r²) : .

В результате, размерность коэффициента тяготения A:

.

53. Уклон удельного эфирного давления в эфировороте

Приравняем усилия тяготения теоретическое и экспериментальное:

-

и найдём из этого уравнения уклон u :

Следовательно, уклон удельного давления эфира в любой точке эфироворота обратно пропоционален квадрату удалённости от центра.

54. Коэффициент тяготения Земного эфироворота

Усилие тяготения F разгоняет предмет с инерцией I в условиях отсутствия торможения с ускорением a :

Подставим в эту формулу выражение для усилия тяготения F:

-

и получим

Отсюда

A = a r².

В качестве опорной позиции выберем поверхность Земли. В этом случае удаление от центра Земли r = 6,37*10⁶ мр; ускорение свободного падения a = 9,81 уск.

Подставим эти значения в формулу и получим численное значение коэффициента тяготения эфироворота Земли:

A_З = 9,81*6,37²*10¹² = 3,98*10¹⁴ уск мр².

Таким образом, усилие тяготения предмета, находящегося в зоне тяготения Земного эфироворота, определяется как

.

Пример. Вычислим усилие тяготения искусственного спутника Земли с инерцией I = 10 тонн = 10⁴ ин, летающего на высоте h = 1000 км = 10⁶ м.

Удаление от центра Земли (от центра эфироворота) составит

r = r_З + h = 6,37*10⁶ + 10⁶ = 7,37*10⁶ мр.

Усилие тяготения определится как

55. Уклон удельного эфирного давления в эфировороте Земли

Подставим в выражение

численное значение коэффициента тяготения эфироворота Земли A_З = 3,98*10¹⁴ уск мр² и получим формулу для расчёта уклона удельного эфирного давления в эфировороте Земли:

.

Напомним, что r – удалённость от центра Земли.

56. Уклон удельного эфирного давления на поверхности Земли

Радиус Земли r_З = 6,37*10⁶ м.

Подставим это численное значение в формулу

и получим численное значение уклона удельного эфирного давления на поверхности Земли:

57. Ускорение свободного падения предмета

Падение предмета может быть свободным только при отсутствии внешних помех, в частности при отсутствии сопротивления воздуха.

Падение тяжёлых предметов, таких как камни, когда их скорость относительно мала (в начале падения), также может рассматриваться как свободное.

В верхних разреженных слоях атмосферы и в свободном космическом пространстве, где нет воздуха, вытеснение предметов к центрам эфироворотов является свободным падением.

Усилие тяготения F предмета с объёмом внутренней пустоты g в зоне тяготения с уклоном удельного эфирного давления u, согласно закону вытеснения пустоты, определяется как

F = u g.

Из соотношения пустоты и инерции

e = g / I = 2б65*10^-8 кбм/ин

извлечём объём пустоты g:

g = e I = 2,65*10^-8*I , -

и подставим его в формулу усилия тяготения:

F = u g = 2,65*10^-8 u I .

Усилие тяготения разгоняет все свободно падающие предметы с ускорением a:

.

Как видно из полученного выражения, ускорение свободного падения предметов не зависит от их инерций, а определяется только уклоном удельного эфирного давления. Свободно падать на землю должны с одинаковым ускорением и камень и пушинка.

Однако в действительности мы наблюдаем совсем иное – камень падает значительно быстрее пушинки. Объясняется это сопротивлением воздуха.

На поверхности Земли усреднённое значение ускорения свободного падения составляет 9,80665 уск и в неточных расчётах может приниматься равным 9,81 уск или даже 9,8 уск.

58. Усилие Земного тяготения предмета

Усилие тяготения вычисляется по формуле

F = u g ,

где u – уклон удельного давления среды, в данном случае – эфирной среды; g – объём тяготеющей (внутренней) пустоты предмета.

Уклон удельного эфирного давления на поверхности Земли u =3,70*10⁸ укл.

Объём тяготеющей (внутренней) пустоты предмета g можно перевести в инерцию I с помощью эквивалента

e = g / I = 2,65*10^-8 :

g = e I = 2,65*10^-8 I .

Усилие тяготения:

F = 3,70*10⁸ *2,65*10^-8 I = 9,8 I .

Получилась та же самая зависимость, какая отражена в выражении

F = a I ,

где a – ускорение свободного падения.

59. Аномалии Земного тяготения

Внутри Земли идёт постоянный рассеянный распад непрочных химэлементов. Он распределён более-менее равномерно по всей планете, но где-то всё же распад - более активный, а где-то - менее активный.

Этим объясняются аномалии Земного тяготения. В одних местах планеты ускорение свободного падения чуть больше 9,81 ускора, в других – меньше.

Аномалия означает отклонение от нормы.

Случаются местные, локальные всплески Земного тяготения. Они вызываются взрывным характером распада.

В жидкой внутренней части Земли идёт медленное расслоение химических веществ: более тяжёлые опускаются к центру планеты; лёгкие всплывают к поверхности. Среди этих слоёв могут собираться химические вещества с непрочными химэлементами. Когда их плотность превышает критическое значение, происходит распадный взрыв.

На месте взрыва резко падает удельное эфирное давление, и это приводит к увеличению уклона этого давления; тяготение в этом месте кратковременно усиливается.

Усиление тяготения бывает настолько большим, что вызывает землетрясения с провалами земли.

Распадные взрывы под океанами и морями вызывают цунами – потоки воды, которые в момент взрыва устремляются к эпицентру взрыва, а потом разбегаются по сторонам.

Усиление местного Земного тяготения вызывают даже взрывы так называемых атомных бомб. При подземных взрывах таких бомб земля в эпицентрах не вспучивается, как при обычных химических взрывах, а проседает, и образуются провальные воронки.

60. Космические скорости

Искусственные спутники Земли удерживаются на круговых орбитах при условии, что имеют окружные скорости, соответствующие радиусам траекторий. Каковы эти скорости?

На спутник действует усилие Земного тяготения F , имеющее следующую зависимость от инерции спутника I и от радиуса его траектории r:

.

Именно это усилие заворачивает спутник и заставляет его двигаться вокруг Земли.

Этому усилию противодействует инерционное, «центробежное» сопротивление R спутника; оно зависит от инерции спутника I , от окружной скорости v и от радиуса траектории r:

Движение спутника по круговой орбите возможно только при условии, когда

F = R .

Приравняем выражения этих величин между собою и определим скорость спутника v:

;

;

.

Примеры.

Определим скорость спутника при движении его по круговой орбите на высоте h = 200 км над землёй.

Радиус Земли r_З = 6370 км.

Радиус круговой орбиты

r = r_З + h = 6370 + 200 = 6570 км = 6,57*10⁶ м.

Подставим численные значения в формулу скорости и получим:

На высоте 300 км скорость будет равна:

На высоте 500 км:

Если скорости спутника окажутся меньше полученных численных значений, то он будет сходить с этих орбит в сторону понижения.

Космические корабли, предназначенные для путешествия в далёкий космос, сначала выходят на круговые орбиты вокруг Земли, а потом уже с них, разгоняясь, уходят дальше.

Характер траекторий космических кораблей в пределах одного эфироворота с повышением скорости движения изменяется: траектория сначала переходит от круговой в эллиптическую, далее – в параболическую и, наконец,- в гиперболическую.

Двигаясь со скоростями параболических и, тем более, гиперболических траекторий, космический корабль преодолевает тяготение планеты и уходит в открытый космос.

61. Удельное эфирное давление в эфировороте

Воспользуемся выражением для уклона удельного эфирного давления в эфировороте Земли:

.

В дифференциальной форме уклон выглядит как

тоесть как изменение удельного давления по удалённости от центра эфироворота.

Чтобы получить выражение для удельного давления p, достаточно проинтегрировать приведённую зависимость по dr:

Приведём интеграл к виду

и найдём по справочнику соответствующее решение:

.

Получим:

.

Постоянная интегрирования C в нашем случае равна максимальному удельному давлению p₀, какое может быть на наибольшем удалении от центра эфироворота; мы его определили равным p₀ = 1,7*10²⁴ уд.

Тогда выражение для удельного эфирного давления Земного эфироворота примет следующий вид:

.

Из выражения следует, что при приближении к Земле удельное давление должно уменьшаться. И оно уменьшается, но столь незначительно, что в наших приблизительных расчётах не может быть обнаружено.

Пример. На том удалении от Земли, на каком находится Луна (r = 3,84*10⁸ м), удельное эфирное давление равно

И такое же практически удельное давление – на поверхности Земли (r = 6,37*10⁶ м):

.

62. Закон сохранения движений

Закон сохранения движений гласит: механические движения не возникают и не исчезают; они лишь переходят из одних форм в другие: из видимых – в невидимые и, наоборот, из невидимых – в видимые.

Иногда такие переходя трудно уловимы.

Рассмотрим такой пример. Предмет падает со стола на пол. У него появляется зримое движение – падение.

Сначала – простой вопрос: в какие движения превратится движение падения при столкновении предмета с полом?

Ответ – лёгкий: движение падения предмета превратится в тепловые движения предмета и пола, тоесть в тепло. В данном случае повышение температуры предмета и пола будет столь незначительным, что наощупь его обнаружить не удастся. Но падающая с большой высоты вода, например с водослива гидростанции, нагревается настолько, что не замерзает даже в лютые морозы.

А теперь – трудный вопрос: а какие предыдущие движения предмета трансформировались в движение падения? Предмет спокойно лежал на краю стола, и у него, вроде бы, не было никаких движений, предшествующих падению.

Чтобы ответить на этот вопрос, вникнем в два аналитических выражения:

;

.

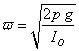Первое выражение характеризует изменение удельного эфирного давления с высотой, а второе – изменение скорости вращения вихревых шнуров химэлементов в зависимости от того удельного давления.

В случае падения предмета высота уменьшается и, как следствие, уменьшается удельное давление эфира. А с уменьшением удельного давления уменьшается и скорость вращения вихревых шнуров тех химэлементов, из каких состоит предмет.

Ответ на поставленный вопрос теперь напрашивается сам собой: при падении предмета часть вихревых движений его химэлементов превращается в движение падения.

А когда мы поднимаем предмет, наши усилия уходят на то, чтобы раскручивать вихревые движения химэлементов этого предмета.

Не имеет смысла приводить в подтверждение сказанного какие-либо расчёты, так как и изменение удельного эфирного давления и изменение скорости вращения вихревых шнуров химэлементов столь незначительные, что обнаружить их нашими расчётами невозможно.

63. Влияние температуры предмета на его тяготение

При повышении температуры предмета его тяготение усиливается.

Однако это усиление настолько ничтожное, что не фиксируется современными средствами измерений.

Покажем это на примере.

Усилие тяготения тонны (кубометра) воды (I =1000 ин) составляет

F = 9,8 I = 9,8*10³ = 9800 сл.

Нагреем воду на 10 градусов и определим увеличение усилия её тяготения.

Теплоёмкость воды

Это означает, что для нагрева одного ина воды на один градус требуется 4,19*10³ движей энергии.

Определим полную энергию нагрева:

ΔE = q I T = 4,19*10³*1000*10 = 4,19*10⁷ дж.

Энергия нагрева ΔE, согласно закону Природы: движения создают пустоту,- увеличит объём внутренней пустоты воды на величину Δg:

где p = 1,7*10²⁴ уд – удельное эфирное давление.

.

Согласно другого закона Природы – закона вытеснения пустоты - усилие тяготения вычисляется по формуле

F = u g ,

где u – уклон удельного давления среды; g – объём пустоты.

В нашем случае усилие тяготения кубометра воды при нагреве её на 10 градусов увеличится на ΔF:

ΔF = u Δg ,

где u = 3,70*10⁸ укл – уклон удельного эфирного давления.

ΔF = 3,70*10⁸*2,46*10^-17 = 9,12*10^-9 сл.

На столько сил увеличится тяготение воды.

Посчитаем степень увеличения усилия тяготения за счёт нагрева:

.

Она ничтожно мала.

64. Плотность инерции и удельное давление воздуха

Воздух атмосферы создаёт своё давление, и оно характеризуется своим удельным давлением и своим уклоном удельного давления.

В отличие от воды, воздух по высоте имеет неодинаковую плотность инерции; с высотой она уменьшается. На высоте в 10 километров, например, она меньше в три раза, чем на земле.

Именно поэтому самолёты дальней авиации летают на этой высоте и выше: там сопротивление воздуха меньше.

С изменением плотности инерции воздуха связано и нелинейное изменение удельного давления воздуха по высоте: на малой высоте оно изменяется более круто.

Для сведения приведём усреднённые значения плотности инерции воздуха и его удельного давления в зависимости от высоты.

Вы сота км	Плотность инерции пин	Удельное давление уд	Вы сота км	Плотность инерции пин	Удельное давление уд
0	1,225	101325	12	0,312	19399
0,05	1,219	100726	15	0,195	12112
0,1	1,213	100129	20	0,089	5529
1	1,112	89876	30	0,018	1197
2	1,007	79501	50	1,027*10^-3	79,8
5	0,736	54048	100	5,55*10^-7	3,19*10^-2
8	0,526	35652	120	2,44*10^-8	2,67*10^-3
10	0,414	26500

И плотность инерции и удельное давление воздуха, на первый взгляд, могут показаться невероятными. Мы привыкли считать, что воздух – невесом, что у него нет никакой инерции. А оказывается, кубометр воздуха имеет инерцию в 1,225 ина и тяготеет к земле с усилием (1,225*9,8) = 12 сил. В комнате с размерами 5х5х3 м содержится 75 кбм воздуха; его инерция составляет почти 100 ин, тоесть больше, чем инерция среднего человека.

Ещё больше поражает нас атмосферное давление.

Возьмём пневматический цилиндр диаметром всего лишь d = 100 мм = 0,1 м, перекроем его полость и попробуем вытянуть шток, создавая в запертой полости вакуум. Препятствовать нам будет удельное атмосферное давление: p = 101325 уд.

Площадь поршня пневмоцилиндра:

Усилие вытягивания F при полном вакууме в запертой полости:

F = p S = 101325*0,00785 = 795 сл.

Это усилие такое же, какое требуется для подъёма взрослого человека.

Особенно удивляет то, какое давление оказывает воздух на тело человека. Суммарная площадь поверхности человеческого тела составляет порядка 3 кваметра. При такой площади общее усилие на человека равно:

F = p S = 101325*3 = 303975 сл.

В пересчёте на рыночные килограммы это составляет 31000 кг, тоесть более 30 тонн.

Удельное давление создаётся тем столбом воздуха, который уходит вверх до пределов атмосферы.

65. Уклон удельного атмосферного давления

Сразу обратим внимание на то, что уклон удельного атмосферного давления направлен не вниз, как у эфирного давления, а вверх. И если эфир выдавливает пустоту вниз, то воздух, наоборот,- вверх. И пустота у них – не одинаковая: в эфире пустота – абсолютная; в неё ничего нет, а в воздухе пустота – вакуум, заполненный эфиром; в нём нет только химэлементов.

Уклон характеризует изменение удельного давления в пространстве: где-то давление больше, где-то – меньше; и разность этих удельных давлений, поделённая на расстояние между указанными точками, и есть уклон.

Основной уклон у воздуха – по вертикали. Но может возникать и горизонтальный уклон; таким он бывает на границе атмосферных антициклонов (с повышенным удельным давлением) и циклонов (с пониженным давлением). Горизонтальные уклоны порождают ветер.

Рассмотрим только вертикальный уклон. Из приведённых данных по плотности и удельному давлению воздуха извлечём удельные давления любых двух соседних точек, определим разность и разделим её на расстояние между этими точками; получим усреднённое значение уклона на выделенном участке.

Просчитаем несколько точек.

1. Интервал между нулевой высотой (h₁ = 0); p₁ = 101325 уд,- и высотой h₂ = 50 м; p₂ = 100726 уд.

Разность давлений

Δp = p₁ – p₂ = 599 уд.

Интервал Δh = h₂ – h₁ = 50 м.

Уклон удельного атмосферного давления на этом интервале составит:

2. Интервал между высотами h₂ = 50 м и h₃ = 100 м; p₃= 100129 уд. Уклон:

3. Интервал между высотами h₃ = 100 м и h₄ = 1000 м; p₄ = 89876 уд. Уклон:

Уклон получился ступенчатым, и всё из-за того, что приняты широкие интервалы высот. В действительности уклон изменяется плавно.

На нулевой высоте он равен приблизительно 12,10 укл и по мере подъёма спадает по убывающей.

66. Подъём тёплого воздуха

Каждому из нас приходилось наблюдать явление подъёма тёплого воздуха вверх. Это – и подымающийся дым над костром, и отклоняющаяся вверх пламя спички, и тепловой поток над газовой горелкой.

Подъём тёплого воздуха вверх – очень важное природное явление. Подтвердим сказанное несколькими примерами.

Циркуляция воздуха внутри помещения. Тёплый воздух от отопительных батарей поднимается вверх, смещается к холодным стенам, охлаждается у них, спускается вниз и возвращается снова к батареям.

Горение. Горячие продукты горения поднимаются вверх, а снизу к пламени устремляется обогащённый кислородом свежий воздух. Если бы продукты горения не уходили от пламени, они перекрывали бы доступ к пламени кислорода, необходимого для горения.

Дыхание. Выдыхаемый тёплый воздух уходит вверх и обеспечивает приток свежего воздуха. Не будь этого, и мы задыхались бы от недостатка кислорода.

Летний дождь. В жаркий летний день нагретый воздух, обогащённый паром, устремляется вверх; там он охлаждается; пар превращается в туман, тоесть в тучу; из тучи начинают выпадать капли дождя.

Круговорот воды на планете. Тёплый влажный воздух экваториальных морей и океанов поднимается вверх, разносится ветром по всей планете, охлаждается, и из него выпадает дождь. Дождевая вода ручьями и реками возвращается снова в моря и океаны.

Полёт воздушных шаров. Пламя горелки согревает воздух внутри шара, и этот нагретый воздух увлекает шар вверх.

В основе явления – подъёма тёплого воздуха вверх – лежат те же основные законы Природы: движения (в данном случае тепловые) создают пустоту и пустота вытесняется под уклон удельного давления среды (атмосферы). Движения и уклон – главные факторы явления.

На космической станции нет естественного уклона удельного давления воздуха, и поэтому там нет само собой возникающего перемешивания воздуха. Чтобы перемешивать воздух, на станциях работают вентиляторы. Иначе космонавты задыхались бы в собственном выдыхаемом воздухе.

Рассмотрим усилие подъёма F, создаваемое тёплым воздухом. Оно имеет следующую зависимость от уклона удельного атмосферного давления u и от объёма дополнительного вакуума Δg, создаваемого тепловыми движениями:

F = u ∆g.

В свою очередь объём создаваемого вакуума Δg определяется как

где E – энергия нагрева; p – удельное атмосферное давление.

В случае с тепловыми воздушными шарами теплота E образуется от сгорания топлива (газа) и определяется как

E = q I ,

где q – удельная теплота сгорания газа; I – инерция сгоревшего газа.

Произведём расчёт теплового воздушного шара. Зададим усилие его подъёма F = 1000 сл (подъём груза весом 100 килограмм).

Удельное атмосферное давление p = 100700 уд.

Уклон этого давления u = 12 укл.

Объём дополнительного вакуума (увеличение объёма шара):

Требуемая энергия нагрева:

E = p Δg = 100700*83 = 8,39*10⁶ дж.

Удельная теплота сгорания газа природного q = 4,5*10⁷ дж/ин.

Расход топлива:

.

Произведённый расчёт – для идеальных условий. В действительности тепловой воздушный шар постоянно охлаждается, и для поддержания требуемой температуры газа внутри него приходится постоянно подогревать воздух; горелку не выключают.

Объём шара не имеет принципиального значения. Он важен только в том смысле, что при большом объёме удержать тепло внутри шара легче. Если же объём шара вообще мал, то создать внутри него дополнительный вакуум объёмом 83 кбм просто невозможно.

Пусть диаметр воздушного шара d = 10 м.

Его объём

V = π d² = 3,14*10² = 314 кбм.

Определим температуру воздуха в нём при подаче на него тепловой энергии E = 8,39*10⁶ дж.

Сначала определим инерцию воздуха внутри шара:

I = ρ V = 1,22*3,14 = 380 ин,

где ρ = 1,22 пин – плотность инерции воздуха.

Учитывая теплоёмкость воздуха , определим повышение температуры ΔT нагретого воздуха в шаре по формуле

.

Если окружающая температура воздуха равна 20 градусам, то температура воздуха в воздушном шаре диаметром 10 метров должна составлять

20 + 22 = 42 градуса.

67. Удельное давление воды

На открытую воду давит воздух, и поэтому удельное давление на поверхности воды определяется атмосферным давлением p = 101325 уд.

Однако на практике обычно атмосферное давление принимается за нулевое, и все приборы для измерения удельных давлений (манометры) настраиваются на этот нуль.

Сохраним такой подход и мы.

Для дальнейших рассуждений выделим в толще воды (речной, морской, океанской) столб воды сечением S. При глубине h объём столба составит

V = S h.

Инерция этого столба воды

I = ρ V = ρ S h

где ρ – плотность инерции воды.

Усилие Земного тяготения выделенного столба

F = 9,8 I = 9,8 ρ S h.

И, наконец, удельное давление p по определению вычисляется путём деления усилия тяготения F на площадь S:

:.

Плотность инерции воды ρ = 1000 пин; с учётом этого:

P = 9,8*1000*h = 9800 h.

Из полученного выражения следует, что удельное давление воды p имеет линейную зависимость от глубины h: во сколько раз изменяется глубина воды, во столько же раз изменяется удельное давление.

На глубине h₁ = 1 м p₁ = 9800 уд.

На глубине h₂ = 2 м p₂ = 19600 уд.

На глубине h₃ = 3 м p₃ = 29400 уд,

и так далее.

Определим глубину h (высоту столба воды), на которой удельное давление воды равно атмосферному:

101325 = 9800 h;

Это означает, что атмосферный воздух давит на каждый квадратный метр площади с тем же усилием, с каким давит водяной столб высотой 10,34 метра.

На глубинах до нескольких десятков метров удельное давление воды соизмеримо с удельным атмосферным давлением, но на глубинах в несколько сотен метров давление воды намного превышает атмосферное.

На глубине h = 500 метров удельное давление воды составляет

p = 9800*500 = 4,9*10⁶ уд,

а на глубине h = 1000 метров удельное давление – в два раза больше:

P = 9800*1000 = 9,8*10⁶ уд.

Это – очень большое давление. Представим себе герметичный бак с размерами 1м х 1м х 1м на глубине h = 1000 м. Площадь каждой из его сторон S = 1*1 = 1 квм. Усилие давления на сторону составит

F = p S = 9,8*10⁶*1 = 9,8*10⁶ сл.

В единицах рыночных килограммов это соответствует миллиону килограммов или тысяче тонн.

Вот почему океанские глубины столь же недоступны людям, как и космос.

В расчётах плотность воды везде принималась постоянной, как будто вода – несжимаемая. Это – не совсем верно: вода, как и любые другие химические вещества, - сжимаема, только степень её сжатия при увеличении давления – очень малая.

68. Уклон удельного давления воды

Ещё раз приведём зависимость удельного давления воды p от глубины h и от плотности инерции ρ:

p = 9,8 ρ h.

Плотность инерции воды изменяется в зависимости от удельного давления по следующему закону:

,

где ρ₀ = 1000 пин – плотность инерции воды в нормальных условиях; β = 4,54*10^-10 1/уд – сжимаемость воды.

Оценим изменение плотности инерции воды в пределах реальных глубин (до 100 метров). Удельное давление на глубине 100 метров составляет приблизительно

P = 9800*100 = 9,8*10⁵ уд.

Плотность инерции при таком удельном давлении изменяется незначительно:

пин.

Поэтому будем считать, что в пределах реальных глубин вода не сжимается и её плотность не изменяется, тоесть ρ = 1000 пин на всех глубинах.

Тогда удельное давление отразится следующей зависимостью:

p = 9,8 ρ h = 9,8*1000 h = 9800 h.

Это выражение мы уже получали.

Из него извлечём уклон удельного давления воды как отношение p / h:

.

Из выражения видно, что уклон постоянен на всех глубинах.

69. Подъём тёплой воды

Тёплая вода, как и тёплый воздух, поднимается вверх.

Такое явление отчётливо наблюдается при нагреве воды на обычной газовой горелке. Кипящая вода буквально бурлит: её струи, насыщенные пузырьками пара, устемляются вверх и способствуют активному перемешиванию воды.

Если же нагревать воду не снизу, а сверху, то ничего подобного не наблюдается: нагретые верхние слои так и остаются наверху, и перемешивания от нагрева не происходит.

По этой причине вода в стоячих водоёмах в жаркие летние дни расслаивается по степени нагрева: сверху – тёплая, а на глубине – холодная.

Усилие подъёма тёплой воды F имеет ту же зависимость от уклона удельного давления воды u и от объёма дополнительного вакуума Δg, создаваемого нагревом:

F = u Δg.

Создаваемый нагревом вакуум рассосредоточен между частицами воды, и только при вскипании он образует пузырьки.

Объём дополнительного вакуума Δg зависит от энергии нагрева E и давления воды p:

.

Сравним усилия выталкивания нагретых сред: воздуха и воды.

Согласно предыдущим расчётам, при подаче на воздух тепловой энергии E = 8,39*10⁶ дж воздушный шар на нулевой высоте создавал усилие подъёма F = 1000 сл.

У воды на глубине h = 10 м суммарное удельное давление воды (9800 h = 98000 уд) и атмосферного воздуха (101325 уд) составит

p = 98000 + 101325 = 199325 уд.

Объём дополнительного вакуума в воде:

.

При уклоне u = 9800 укл усилие подъёма воды F на глубине h = 10 м определится как

F = u Δg =9800*42,09 = 4,13*10⁵ сл,

тоесть в 413 раз больше, чем у воздуха.

Но вот – парадокс: при увеличении глубины усилие подъёма нагретой воды не увеличивается (как казалось бы), а уменьшается.

Такой вывод следует из анализа выражения для усилия подъёма F при подстановке в него формулы для определения дополнительного объёма Δg и зависимости удельного давления p от глубины h (на больших глубинах):

.

Определим усилие подъёма воды на глубине 100 метров при подаче на неё той же тепловой энергии E = 8,39*10⁶ дж:

Усилие подъёма уменьшилось почти в 5 раз:

4,13*10⁵ / 8,39*10⁴ = 4,9.

Следовательно, перемешивание воды на больших морских и океанских глубинах при нагреве со дна (например терминальными источниками) выражено гораздо слабее, чем близко к поверхности.

70. Выталкивание предметов из воды и воздуха

Каждый из нас замечал, что тяжёлые предметы в воде становятся легче. Объясняется это тем, что вода выталкивает предметы вверх.

Предметы выталкиваются из любой среды. В земных условиях уклон удельных давлений воды и воздуха есть всегда, но на космической станции, в условиях невесомости вода, например, его не имеет, и поэтому она не выталкивает предметы никуда.

Усилие выталкивания можно посчитать двояким способом: обычно – через уклон и в частном случае – через объём предмета.

Начнём со второго способа. Его частный характер состоит в том, что он применим только в случае открытой стоячей воды. Для жидкостей, движущихся с ускорением или находящихся во вращении, он непригоден.

Возьмём небольшую ёмкость, заполненную водой, и будем опускать в неё предмет. Нетрудно заметить, что уровень воды в ёмкости при этом повышается. Если же предмет извлекать из воды, её уровень будет понижаться.

Создаётся впечатление, что предмет и вытесняемая им вода как бы находятся на разных чашах рычажных равноплечих весов: опускается предмет – поднимается вода; поднимается предмет – опускается вода.

Объясняется всё тяготением Земли: предмет тяготеет к Земле с усилием F_ПР; вытесняемая им вода тяготеет с усилием F_B в объёме предмета.

Допустим, что предмет – лёгкий; его плотность инерции ρ_пр меньше плотности инерции воды ρ_В. Такой предмет будет всплывать, и усилие всплытия определится как

ΔF = F_В – F_ПР .

Усилие тяготения вытесняемой воды F_В определяется по формуле

F_В = 9,8 I_В = 9,8 ρ_В V_ПР,

где I_В – инерция вытесняемой воды; V_ПР – объём предмета.

С учётом этого определим усилие всплытия предмета:

ΔF = 9,8 ρ_В V_ПР – F_ПР.

Запомним это выражение и повторим расчёт по закону вытеснения пустоты.

У погружённого в воду предмета по сравнению с водой имеется дополнительный объём вакуума Δg ; именно поэтому плотность инерции предмета меньше плотности инерции воды.

Усилие всплытия по закону вытеснения пустоты определяется как

ΔF = u_В Δg,

где u_В – уклон удельного давления воды; он нами ранее определён и равен u_В = 9,8 ρ_В.

Если бы объём предмета V_ПР был меньше на Δg, а инерция I_ПР оставалась бы прежней, то его плотность инерции равнялась бы плотности инерции воды:

.

Извлечём из данного выражения Δg:

I_ПР = ρ_В V_GH – ρ_В Δg; ρ_В Δg = ρ_В V_ПР – I_ПР;

.

Подставим значения u_В и Δg в формулу усилия всплытия предмета ΔF:

;

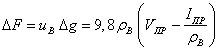ΔF = 9,8 ρ_В V_ПР – 9,8 I_ПР;

ΔF = 9,8 ρ_В V_ПР – F_ПР.

Получили то же самое выражение, какое было при первом расчёте. Только теперь выталкивание предмета уже – не вверх, а под уклон удельного давления воды.

Если погружаемый в воду предмет – тяжёлый (его плотность инерции больше плотности инерции воды), то в полученном выражении поменяются знаки:

ΔF = F_ПР – 9,8 ρ_В V_ПР.

Теперь уже ΔF – не усилие всплытия, а усилие погружения.

В общем случае, применительно к любой текучей среде это выражение можно записать так:

ΔF = F – 9,8 ρ V,

где F – усилие тяготения предмета; ρ – плотность инерции среды; V – объём выталкиваемого предмета.

Здесь (9,8 ρ V) – усилие выталкивания предмета.

Пример.

Определим усилие погружения в воду стального предмета с инерцией 10 ин; плотность инерции стали ρ_СТ = 7,8*10³ пин; плотность воды ρ = 10³ пин.

Объём предмета:

.

Усилие тяготения предмета:

F = 9,8 I = 9,8*10 = 98 сл.

Усилие погружения предмета в воду:

ΔF = F – 9,8 ρ V = 98 – 9,8*10³*1,28*10^-3 = 85,5 сл

Усилие тяготения стального предмета уменьшилось на

(98 – 85,5) = 12,5 сл,

тоесть на

(12,5 / 98)*100 % = 12,8 %.

71. Вес

В быту усилие тяготения предметов называется весом. Единицей веса является килограмм: 1кг = 9,8 сл.

Кроме собственно усилия тяготения предмета, вес учитывает также выталкивание предмета воздухом и инерционное сопротивление от вращения Земли. Оценим влияние того и другого.

Возьмём 10 ин картошки; плотность инерции картошки ρ_К = 1,1*10³ пин.

Усилие тяготения картошки вниз

F = 9,8 I = 9,8*10 = 980 сл.

Объём картошки

.

Плотность инерции воздуха ρ = 1,29 пин.

Усилие выталкивания картошки воздухом вверх

F_В = 9,8 ρ V = 9,8*1,29*9,09*10^-3 = 0,115 сл.

Инерционное сопротивление от вращения Земли больше всего сказывается на экваторе, где окружная скорость Земли составляет v = 463 ск. Радиус Земли r = 6,37*10⁶ м.

Инерционное сопротивление повороту направлено вверх и рассчитывается по формуле:

.

В результате усилие Земного тяготения картошки F = 980 сл уменьшится на суммарную величину

F_В + F_ИС = 0,115 + 0,337 = 0,452 сл,

что в процентах составляет

(0,452 / 980)*100 % = 0,046 %

.

Поправка (0,046 %) столь мала, что можно вес в килограммах численно приравнивать к инерции в инах. В нашем случае 10 ин картошки весят 10 килограмм.

72. Течение жидкостей по трубопроводам

Можно упомянуть водопровод, нефтепровод; очень широко распространены гидравлические системы машин, где жидкости используются в качестве энергоносителя и где они передаются от узла к узлу по трубопроводам.

Нагнетаются жидкости насосами. Они создают подпор давлений. От подпора по всем магистралям возникают уклоны давлений. Жидкости смещаются под эти уклоны.

Различают два вида течения: гладкое (ламинарное) и вихревое (турбулентное).

При гладком течении сдвиговая скорость - постоянная, начиная от стенок трубопровода и кончая осью трубы, и поэтому частицы жидкости движутся по прямолинейным траекториям (параллельно стенкам).

Уклон удельного давления u гладкого течения имеет линейную эмпирическую зависимость от средней скорости по трубе v:

.

Здесь ζ (греческая дзэта) – коэффициент гидравлического сопротивления гладкого течения, зависящий от диаметра трубопровода, от характеристик текущей жидкости и от температурных условий течения. Размерность

.

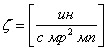Сдвиговая скорость у стенок трубопровода имеет свой верхний предел, после которого пристенный слой жидкости начинает отставать и вынуждает последующие слои заворачивать к стенкам; прямолинейность потока нарушается, и течение из гладкого превращается в вихревое. Переход от гладкого (ламинарного) течения к вихревому (турбулентному) – ступенчатый с гистерезисом. Гистерезис означает, что переход от гладкого течения к вихревому происходит на большей скорости, чем при обратном переходе – от вихревого к гладкому.

Уклон удельного давления u вихревого течения имеет квадратичную эмпирическую зависимость от средней скорости по трубе v:

,

где ξ (греческая кси) – коэффициент гидравлического сопротивления, но уже – вихревого течения.

Размерность коэффициента гидравлического сопротивления:

.

Содержание

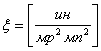Напоминание

1. В предыдущем учебнике

2. Некоторые физические величины

Вычисления 

1. Точность вычислений

2. Эфирный шарик как фундаментальная единица измерений

3. Инерция эфирного шарика

4. Инерция электронной секции вихревого шнура химэлемента

5. Инерции титульных химэлементов

6. Длина вихревого шнура химэлемента протия  в единицах

7. Диаметр химэлемента протия  в единицах дш

8. Длина вихревого шнура химэлемента лития  в единицах дш

9. Диаметр химэлемента лития  в единицах дш

10. Объём химэлнмента лития  в единицах дш³

11. Объём химэлемента лития  в единицах кбм

12. Диаметр эфирного шарика

13. Объём эфирного шарика

14. Плотность инерции эфирного шарика

15. Плотность инерции эфира

16. Аналитические зависимости световых волн

17. Скорость и путь равноускоренного движения

18. Энергия движения предмета

19. Энергия фотона

20. Размерности должны сходиться

21. Амплитуда световой волны

22. Ускорение эфирных шариков при срыве световой волны

23. Удельное давление эфира

24. Численное значение энергии фотона

25. Объём пустоты фотона

26. Уклон удельного эфирного давления в пришнуровой зоне химэлемента

27. Энергия распада химэлементов

28. Внутренняя энергия предмета

29. Пустота эквивалентна энергии

30. Эквивалент инерции и внутренней пустоты предмета

31. Объём внутренней пустоты химэлементов

32. Объём внутренней пустоты электронной секции химэлемента

33. Объём шариковой оболочки электронной секции

34. Отношение объёма внутренней пустоты к объёму оболочки электронной секции

35. Объём электронной секции

36. Наружный диаметр вихревого шнура химэлемента

37. Внутренний диаметр вихревого шнура химэлемента

38. Осевые усилия вихревых обрывков

39. Усилие радиального раздавливания вихревого обрывка

40. Инерция поворота – аналитическая зависимость

41. Инерция поворота электронной секции химэлемента

42. Внутренняя энергия электронной секции химэлемента

43. Энергия вращения предмета

44. Скорость вращения вихря химэлемента

45. Продолжительность одного оборота вихревого шнура химэлемента

46. Объём внутренней пустоты электрона

47. Тяготение электрона

48. Инерционное сопротивление при движении предмета по кривой траектории

49. Тяготение планет

50. Эфировороты

51. Усилие тяготения в эфироворотах

52. Экспериментальная закономерность тяготения предметов в эфироворотах

53. Уклон удельного эфирного давления в эфировороте

54. Коэффициент тяготения Земного эфироворота

55. Уклон удельного эфирного давления в эфировороте Земли

56. Уклон удельного эфирного давления на поверхности Земли

57. Ускорение свободного падения предмета

58. Усилие Земного тяготения предмета

59. Аномалии Земного тяготения

60. Космические скорости

61. Удельное эфирное давление в эфировороте

62. Закон сохранения движений

63. Влияние температуры предмета на его тяготение

64. Плотность инерции и удельное давление воздуха

65. Уклон удельного атмосферного давления

66. Подъём тёплого воздуха

67. Удельное давление воды

68. Уклон удельного давления воды

69. Подъём тёплой воды

70. Выталкивание предметов из воды и воздуха

71. Вес

72. Течение жидкостей по трубопроводам

Антонов

Владимир Михайлович

Физика. Русский вариант / Учебник 3 – Физика вычислительная. 2008

Редактирование авторское

---

Турбореактивные двигатели

---